ПОДХОД К РАСЧЕТУ ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗЛИЧНЫХ ТИПАХ НЕСИММЕТРИЧНЫХ АСИНХРОННЫХ ДВИГАТЕЛЕЙ С УЧЕТОМ ИЗМЕНЕНИЯ ПАРАМЕТРОВ
Автор:Д.А.Тонн
Доцент Международного института компьютерных технологий, г. Воронеж
Рассматривается подход к расчету переходных процессов в различных типах несимметричных асинхронных двигателей с учетом изменения параметров их схем замещения по экспоненциальным зависимостям, полученным по результатам расчета магнитного поля.
Асинхронные машины с несимметрией ста- тора находят широкое практическое примене- ние, в то время как машины с несимметрией ротора практически не используются [1].
Несимметричные электрические машины обладают существенной нелинейностью связей физических явлений, протекающих в них, даже в установившихся режимах работы. Это следует обязательно учитывать при их математическом описании, что значительно усложняет анализ режимов работы таких машин.
Типичным примером однофазной асинхронной машины с несимметрией статора может служить конденсаторный асинхронный двигатель (КАД). КАД — это асинхронный двигатель который имеет на статоре две фазные обмотки сдвинутые в пространстве на 90° электрических градусов (т.е. = ? 90°), и симметричный короткозамкнутый ротор. Одна из обмоток статора (главная) включается непосредственно в однофазную сеть, а другая обмотка (вспомогательная) включается в эту же сеть, но через фазосдвигающий элемент, чаще всего его роль выполняет рабочий конденсатор. Физические процессы, протекающие в различных режимах работы КАД, носят сложный характер и представляют собой электромеханические переходные процессы, так как при этом происходит одновременное изменение скорости вращения и электромагнитных характеристик двигателя.
При составлении математической модели несимметричных асинхронных двигателей (АД) в качестве исходного как наиболее общий случай рассмотрим однофазный асинхронный двигатель (ОАД) с общей несимметрией статора, которая выражается в неравенстве параметров фаз статора, в отличии угла между осями обмоток статора от 2п/m электрических радиан, в неравенстве числа витков фаз статора. Путем принятия ряда допущений уравнения рассмотренного ОАД могут быть просто преобразованы в уравнения КАД, имеющего различные схемы включения, в уравнения других типов ОАД или даже в уравнения трехфазных асинхронного двигателя, работающих в различных схемах однофазного включения.
Система дифференциальных уравнений, описывающая поведение асинхронного двигателя с общей несимметрией статора включает в себя уравнения равновесия напряжений обмоток и уравнение движения электропривода [1]. При составлении уравнений равновесия напряжения сначала целесообразно использовать фазовую (естественную) систему координатных осей. При этом предполагаем, что обмотка ротора приведена к обмотке статора. Дифференциальные уравнения двухфазной асинхронной машины с общей несимметрией статора в естественной (фазовой) системе координат содержат периодические коэффициенты, что существенно затрудняет решение системы. С целью снижения объема вычислений и ускорения практических расчетов данную систему уравне- ний нужно преобразовать в систему с постоянными коэффициентами.
Для того чтобы избавиться от периодических коэффициентов в уравнениях, обычно применяют метод преобразования координат, то есть используют их линейные преобразования. Преобразование координат позволяет упростить уравнения и получить постоянные коэффициенты перед переменными, но не уменьшает число уравнений системы.
Дифференциальные уравнения, описывающие работу электрической машины, имеют постоянные коэффициенты только в том случае когда оси обмоток статора и ротора неподвижны друг относительно друга. Уравнения электрической машины могут быть записаны в различных системах координатных осей [2]. Считается, что в электромехнике существует бесчисленное число систем координат, но на практике находят применение лишь наиболее удобные.
Для двухфазной асинхронной машины с общей несимметрией статора избавиться от периодических коэффициентов можно, записав ее уравнения в ортогональной системе координат, неподвижной относительно статора, то есть в системе координат a,b. В этом случае в любой момент времени реальные переменные ротора заменяются их проекциями на оси статорных обмоток.
Полученные при этом уравнения записаны уже в неподвижных координатных осях, которые жестко связаны с обмоткой статора. Следует отметить, что такое преобразование воз- можно лишь в том случае, когда ротор симметричен. Эта система уравнений уже не содержит периодически изменяющихся во времени коэффициентов. Для получения решения численными методами с применением вычислительной техники необходимо представить эту систему в нормальном виде. Для этого нужно ре- шить систему уравнений (3) относительно токов и подставить их значения в (1) , а также выразить электромагнитный момент эм M через потокосцепления и параметры машины.
Система дифференциальных уравнений ОАД с общей несимметрией статора в системе координат a,b и в относительных единицах имеет следующий вид:
Связь между токами обмоток и потокосцеплениями устанавливается уравнениями:
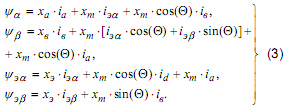
Применение математического моделирования на стадиях проектирования и изготовления макетных и опытных образцов позволяет разработчику уже на этих этапах рассматривать
динамику машины, оценивать ее пусковые и эксплуатационные свойства, что значительно снижает затраты на макетное моделирование и сокращает срок разработки. Приведенная модель несимметричного АД служит для изучения и оптимизации сложных нелинейных процессов, исследование которых традиционными способами затруднено или невозможно.При математическом моделировании обычно принимают параметры, входящие в уравнения постоянными. Такое упрощенное представление параметров при решении целого ряда задач нежелательно и может исказить результаты.
Учет изменения параметров с течением времени особенно важен, когда при переходных процессах скорость двигателя изменяется в широких пределах, что весьма характерно для ОАД и КАД в частности.
В течение переходного процесса картина электромагнитного поля не остается постоянной, а вместе с ней изменяются и значения параметров схемы замещения. В несимметричных ОАД малой мощности наибольшее влияние на изменение параметров оказывают насыщение магнитной цепи двигателя. Насыщение магнитной цепи следует учитывать во всех типах несимметричных АД.
Определение зависимостей изменения параметров несимметричных АД затруднено из-за отсутствия отработанных методик расчета и экспериментальных исследований, хотя необходимость определения таких зависимостей существует уже давно. Для нахождения таких зависимостей необходимо определить значения параметров в статических режимах работы. На этом этапе следует применять средства анализа электромагнитных полей.
При моделировании несимметричных АД магнитное поле можно рассчитывать в попе речном сечении. Исследуемый двигатель можно моделировать в режимах установившегося короткого замыкания, холостого хода и номинальном. Для расчета электромагнитного поля в этих режимах целесообразно использовать метод конечных элементов реализованный в универсальном конечно-элементном пакете ANSYS.
На основании полевых расчетов можно определить зависимости индуктивных параметров схемы замещения исследуемого типа несимметричного АД от времени в течение электромеханического переходного процесса.
Такие зависимости приводятся в [1]. При этом следует руководствоваться гипотезой, которая получила экспериментальное подтверждение [1], что индуктивные параметры схемы замещения АД изменяются по экспоненциальной зависимости, в качестве показателя степени которой используется электромеханическая постоянная времени АД.
Определенные зависимости необходимо подставлять в математические модели различенных типов несимметричных АД, которые в свою очередь получают из математической модели двухфазной асинхронной машины с общей несимметрией статора.
Построенные таким образом математические модели несимметричных АД малой мощности, содержащие в себе решение электромагнитного поля, могут быть использованы специалистами в области электрических машин и инженерами-электриками при проектировании и расчетах таких двигателей.
Это является, с одной стороны, существеным уточнением существующих математических моделей, базирующихся на схемах замещения, а с другой – органичным развитием последних. Наилучшие результаты при проектировании дает совместное применение математического моделирования и экспериментальных исследований опытных образцов ОАД.
Литература
1. Тонн Д. А. Квазиустановившиеся и переходные процессы несимметричных асинронных двигателей, работающих от однофазной сети: Автореферат дис. канд. техн. наук. / Тонн Д.А. – Воронеж: ВГТУ, 2004. – 17 с.