Snegina
E., Pougatch A., Khomenko
V., Melnyk A., Henaff P., Borysenko V.
Practical aspects of
Rowat-Selverston
bio-inspired oscillator
simulation
The paper deals with practical aspects of the Rowat-Selverston biologically
inspired oscillator simulated using modern research software. Most significant
errors were estimated and their impact on the neuron dynamic behavior was systematized.It permitted us to develop a rational high-performance simulation
algorithm. The oscillator was implemented using C++ language and tested on a
real-time system (industrial electronic unit controller BIA of a biped robot).
Introduction. Models of neural system were started to be used to
resolve practical technical problems since 60-s of the XX century when the
first “neuronal” electrical calculating machines were
constructed. Their main difference is in the use of tuned ceil elements
with weighed instead of a formal logic (AND, OR, NOT etc.) [1]. These elements are usually connected in a specified network
called “neural network”. Perceptrons are a class of
neural network corresponding to the acquisition and treatment of information in
a feedforward scheme, this capacity is already well
studied. Nowadays the interest of research is concentrated on the class of
oscillatory neurons corresponding to the capability of an organism to execute
and learn rhythmic movements.
The
presented work is connected with an actual problem of modeling
and simulation of central pattern generator neurons [2] that produce rhythmical
movements observed in the living creatures. Using this way for movements
production of humanoid robots should be the most natural when they interact
with ambient environment or human. The input of a neuron is a current impulse
that can start or stop oscillations of his membrane potential. Frequency and
amplitude of oscillations, for a concrete organism, are determined by its
chemical state that is achieved in technical systems by variation of model
parameters. An idea of the work consists in the choice of
appropriate methods of calculation of a Rowat-Selverston oscillator model [2, 3]. This one
is a good approximation of a neuron that generates rhythmic movements in
biological organisms. Different scientific software was applied that permitted
to determine the most appropriate of them for the analysis of theoretic aspects
of his dynamic behavior, and also for his practical realization (with robots
ROBIAN biped [4] and KATANA-NEURONIX arm [5]).
The objective
of this work is to compare several methods in the calculation of the Rowat-Selverston model according to the criteria of minimum
calculation time, and the possibility of direct transition to its physical
realization. The task
considered the model calculation with different tools assuming the same
parameters of a model was posed to achieve the formulated objective. Next tools
were used: 1) continuous-time blocs of Simulink MATLAB; 2) scrip language of
MATLAB; 3) programming language C++. The originality of received
results consists in experimentally determined differences between simulation
results of these different scientific calculation methods.
Calculation errors were evaluated and reaction of the neuron model on the
several typical inputs (impulse, step, sinus, meander) was established, that permitted to determine its
dynamical properties.
In the
first part of this article the mathematic model of a neuron is presented and
activation curves are analyzed. The second part explains three principles of
simulation of the model, one of them with practical application to a real biped
robot [4]. Simulations show that maximum errors in phase and in absolute value
of oscillations appear due to approximations of the model for real-time
application. The final third part shoes different comportments of an oscillatory
neuron.
Mathematic model of Rowat-Selverston
oscillator.
Biological
neurons with several canals have complicated structure that creates
difficulties in their modeling. American scientists Rowat
and Selverston [2, 3] have presented (in 1997) an
approximated model of such neuron. They took into account two groups of
currents (“slow” and “fast”) and proposed two first order differential
equations connecting currents and tensions [2]. The fast current is described
by equation (1) and the slow – by equation (2):
,
(2)
where 
, 
is the neuron membrane time constant; 
is the time constant of a slow activation of currents;
is an injected current; U is a membrane
tension; q is a slow current; U and q are variables; 
is a nonlinear voltage-current
characteristic of the fast current determined by the next equation [2]:
.
(3)
Function 
is a fundamental part of a Rowat-Selverston
model because, depending on the current gain
, it determines different comportment of the
oscillator [2, 3, 6, 7] (attenuating oscillations, aperiodic or oscillating without
attenuation). Characteristics can be linear when 
, nonlinear bijective
[8] when 
, and nonlinear nonbijective
when 
(fig. 1.a).
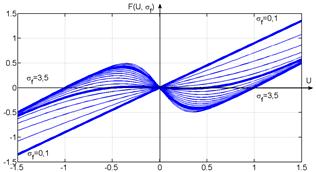
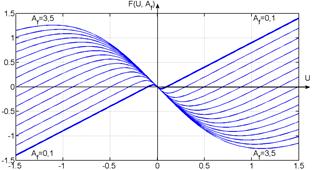
a)
b)
Figure 1 –
Characteristics for several values of: a) current gain , 
; b) coefficient 
, 
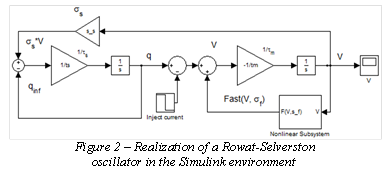
Simulation procedure of an oscillating neuron. According
to equations (1) and (2) a model was constructed in Simulink MATLAB (fig.
2) with formula (3) used to solve the fast part of the equation. Values of
constants [2] are the next ones: Af = 1; σf
= 3; τs = 1; τm = 1/20.
The
oscillator model description using Matlab script
language was established. The numeric integration method ode45 with automatic
step adaptation was used:
clc, clear all; close all;
X0=[0;0]; interval=[0:0.001:10];
global flag
flag=1;
[T,X]=ode45('funcRS',interval,X0);
plot(T,X(:,1),':',T,X(:,2),'-'),grid
on,legend('V','q'),xlabel('t, s')
function F=funcRS(t,x)
global flag
Af=1.0;tm=1/20;ts=10; ss=3;sf=1.6;
Iinj=funcIinj(flag); Es=0;
F=[-1/tm*(-Iinj+x(2)+(x(1)-Af*tanh(x(1)*sf/Af)));
1/ts*(-x(2)+ss*(x(1)-Es))];
function O=funcIinj(flag)
if flag == 1, O = 1.6; else O = 0; end
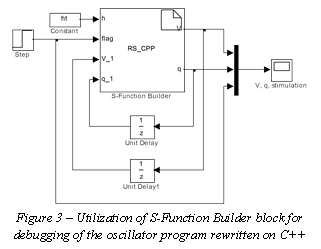
For the С++ program debugging we used the S-Function
Builder block (fig. 3). The neuron start signal was applied to its input (flag).
Current and membrane potential were delayed for one period of sampling time. It
is needed to solve numerically differential equations of a neuron (with firs
order Euler method). The next program was optimized, that consists in usage of
a table th function
(100 points) and interpolation between neighbor points instead of a standard
library function.
float i_inj, A_f,
sig_f, E_s, sig_s, TM, TS,
u[101], th[101], u1, t, q_inf,
i_fast, i;
u1=V_1[0]*sig_f/A_f;
if (flag[0] == 1), i_inj =
1.6;
else i_inj = 0;
A_f=1.0; sig_f=1.0;E_s=0.0;sig_s=3;
TM=1.0/20.0;TS=10.0;
if ((V_1[0]-E_s)>=0)
q_inf=sig_s*(V_1[0]-E_s);
else
q_inf=0.5*sig_s*(V_1[0]-E_s);
u[0]=-5.00;… th[0]=-0.99990920;…
for (i=0;i<=49;i++)
{ if (u1<=u[i]),
break; }
if (i>=50)
for (i=100;i>=49;i--)
{ if (u1>=u[i]), break; }}
if (i==0), t=th[0];
else { if (i>=100),
t=th[100];
else
{ if (i<50), t=(th[i]-th[i-1])*((u1-u[i-1])*10.0)+th[i-1];
else { if (i>=50), t=(th[i+1]-th[i])*((u1-u[i+1])*10.0)+th[i+1];}}}
i_fast=V_1[0]-A_f*t;
q[0]=q_1[0]+h[0]*((q_inf-q_1[0]))/TS;
V[0]=V_1[0]+h[0]*(-(-i_inj+q_1[0]+i_fast))/TM;
The
simulation error using standard mathematic library functions (with double
precision) and С++ program (with float precision, as processor modules
of robots [4] and [5] are limited):
а)
б)
Figure 4 –
Instantaneous errors analysis of the С++ neuron model:
а) using functions of a hyperbolic
tangent from a standard mathematic library (math.h);
б) with linear interpolation of a hyperbolic tangent table
function (100 points method)
Using the
hyperbolic tangent function th from
standard mathematic library (fig. 4.a), the instantaneous error of the membrane
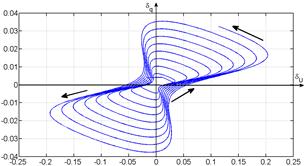
potential does not exceeds 3%, and the current 0,4%.
The frequency of generated impulses coincides with precise solution of the system of equations
(1)-(3). This can be seen from asymptotic convergence of a curve (fig. 4.a),
that is more evident for a high number of oscillations. The
root-mean-square error is 0,213% for the tension and 0,069% for the
current. The error of hyperbolic tangent approximation (using table function
with interpolation between points) leads to a variable error in oscillation
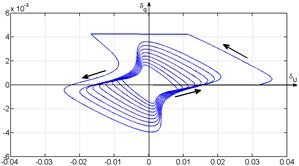
phase (for the considered case the first maximum of the error, equal to π radian, the maximum is reached at the time 589,5s, lineary rising with speed of 1,696·10-3 π/s, fig.
5). The corresponding graphic of an instantaneous error (fig. 4.b) diverges
when the error increases. The root-mean-square error, practically, does
not changes (0,231% for tension and 0,042% current).
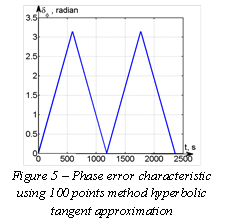
These results can be
considered as acceptable because the influence of hyperbolic tangent
approximation has mostly effect on the phase of generated oscillations (linear
periodic phase drift), but not on their absolute values. Increase of a number
of table points of th
does not rational as it increases the time necessary to make calculations,
moreover the maximum length of the data array in the memory of the industrial
controller is limited. Nevertheless, usage of tables permits to liberate
resources of the mathematical co-processor of the controller to resolve more
complex problems of robot
control (calculation of his geometric and dynamic models).
Analysis of the simulation results. Taking into account information presented
above on the simulation precision, we study behaviors of the Rowat-Selverston oscillators from typical inputs. The model
(fig. 2) was used. Results are presented in
relative coordinates on (fig 6.a-d).
|
a) |
b) |
|
c) |
d) |
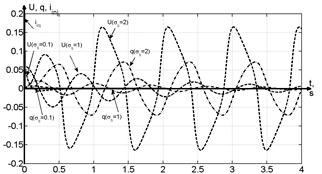
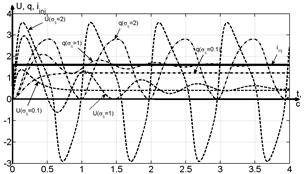
Figure 6 –
Reaction of on oscillator on different inputs:
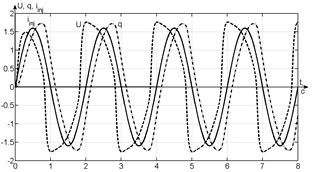
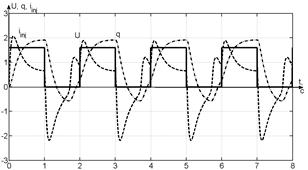
а) impulse;
б) step; в) sinus (T=0,5s); г) meander (T=0,5s).
The parameter 
influence mostly on the amplitude of
oscillations for higher tensions U, so graphics (fig. 6.a-b) are
presented for several values of 
with fixed Af
= 1; τs = 1; τm = 1/20.
Oscillations
with different features were received: a) relaxation non-harmonic with
frequency 1,11Hz for impulse input; b) aperiodic with constant time 0,25s for
step input; c) quasi-harmonic periodic for sinusoidal input; d) nonharmonic periodic for meander input.
These
simulation results showed characterize basic regimes of the Rowat-Selverston
oscillator [3], present its ability to generate as
periodical as and aperiodic signals. In this case synchronization with periodic
input (sinus, meander) is not typical for biological systems, where “spiking” of neuron is controlled by
discrete impulses of current (as shown on the fig. 5.a).
The
considered simple model of the artificial oscillator does not take
into account certain properties of its biological original – the neuron
of a central pattern generator. For example, time delays that influent on the
dynamics of a system; input signals actuate directly output of the oscillator.
And, what is even more significant, one separate oscillator does not take into
account synchronization function of a biological neuron, considered by most of
researchers in the domain as principal. This phenomenon is used to generate
rhythmic movements of anthropomorphic robots, as it represents a natural for a
human procedure of interaction with its environment (gesticulation, periodic
repeating actions etc.). However, there are publications justifying that the
property of autosynchronization is intrinsic for a
pair of Rowat-Selverston oscillators. This case is
typical for biological systems, and will be a subject of our future researches.
Resume.
1. Using of a
table function of a hyperbolic tangent for a real-time realization of Rowat-Selverston oscillator almost does not influence on
the root-mean-square error, but is manifested as a low frequency phase
modulation of the oscillator output signal. 2. The
most comfortable, between considered ways of simulation of the oscillator, is
MATLAB Simulink; the highest speed of calculation is received for program
written on С++. 3. As there are no
operations of differentiation in the model, it is possible to use as double
precision numbers, as and single precision.
BIBLIOGRAPHY
1. Галушкин А.И. Теория нейронных сетей. Кн. 1.: Учеб. Пособие для вузов / Общая ред. А.И. Галушкина. – М.: ИПРЖР, 2000. – 416 с.: ил. (Нейрокомпьютеры и их применение). – ISBN 5-93108-05-8.
2.
Rowat P.F., Selverston A.I. Oscillatory mechanisms in pairs of neurons
connected with fast inhibitory synapses // Journal of Computational Neuroscience 4. – Kluwer Academic Publishers, 1997. – 25 с.
3.
E. Amrollah, P. Henaff. On the role of sensory feedbacks in Rowat–Selverston CPG to improve
robot legged locomotion
// Frontiers Neurorobotics 4, 113,
2010. – 9 с.
4. A. Konno, R. Sellaouti, F.B.
Amar, F.B. Ouezdou, Design and development of the
biped prototype ROBIAN // Proceedings – IEEE International Conference on
Robotics and Automation. – Vol. 2. – 2002. – pp. 1384-1389.
5. Katana 450 Benutzerhandbuch. Neuronics AG. – Document Nr: 233493. – Version 2.0.4. – 2001-2008.
6. А.П. Кузнецов, С.П. Кузнецов, Н.М. Рыскин. Нелинейные колебания. Учеб. пособие для вузов. – М.: Издательство физико-математической литературы, 2002. – 292 с.
7. С.Ю. Кириллов, В.В. Клиньшов.
Исследование динамических режимов модели нейрона с последеполяризацией
// Труды научной конференции по радиофизике. – ННГУ, 2007. –
86 с.
8. Н.К. Верещагин, А. Шень Часть 1. Начала теории множеств. Лекции по математической логике и теории алгоритмов. — 2-е изд., испр. — М.: МЦНМО, 2002. — 128 с.