Ludovic Righetti, Jonas Buchli, Auke Jan Ijspeert

Автор перевода – Е.А. Снегина

Динамические правила обучения Хебба  адаптации частот осцилляторов

         Источник: Physica D, vol. 216, num. 2, 2006, p. 269 – 281.

         Режим доступа: http://www.robotcub.org/misc/papers/06_Righetti_Buchli_Ijspeert.pdf

       Аннотация

      Нелинейные осцилляторы широко используются в биологии, физики и технике для моделирования и контроля. Они интересны своими свойствами синхронизации в сочетании с другими динамическими системами. В этой статье  предлагаются правила обучения осцилляторов, адаптации их частоты к  частоте любого периодического или псевдо периодического входного сигнала. Обучение проводится по законам динамики: осциллятор является частью динамической системы, а не независимого процесса. Интересной особенностью модели является то, что она легко обобщает в себе широкий класс осцилляторов, от фазовых осцилляторов до релаксационных и неизвестных аттракторов с общим правилом обучения. Одной из основных особенностей нашего  обучения является то, что созданные осцилляторы могут адаптировать свои частоты без какой-либо обработки сигнала, без необходимости указывать временное окно или аналогичные переменные параметры. Вся обработка встроена в динамике адаптивного осциллятора. Сходимость обучения доказана для осциллятора Хопфа, где численные эксперименты проводятся с целью изучения возможности обучения системы. Наконец, мы обобщаем правило обучения негармонических осцилляторов, таких как релаксационные и неизученные.

      1 ВВЕДЕНИЕ

       Нелинейные осцилляторы широко используются для моделирования различных физических и биологических процессов, а в течение последних двух десятилетий, они также используются в инженерных разработках, например, автономных роботов. Модели джозефсоновских переходов [22], лазеры, центральный генератор паттернов (англ. CPGs) [6,10,13,23], ассоциативная память [2,18] или восприятие удара [8,14] являются несколькими примерами, которые показывают значение осцилляторов в области моделирования и управления.

     Модели осциллятора  интересны своими возможностями синхронизации или с другими осцилляторами или с внешними воздействующими сигналами. В большинстве случаев это является трудной задачей правильного выбора параметров осцилляторов, чтобы обеспечить их свойства синхронизации на необходимом уровне. Большинство исследований используют фазово-охватывающее поведение, но когда параметры находятся вне фазово-охваченной области синхронизации, синхронизация не удается. В основном это происходит по причине того, что осцилляторы теряют пластичность, они имеют фиксированные собственные частоты и не могут динамически адаптировать свои параметры.

        Некоторые недавние исследования, однако, сосредоточиваются на развитии динамической пластичности для осцилляторов, так что они могут учиться и синхронизировать с более широким диапазоном частот без необходимости настраивать параметры вручную [1,2,9,15 – 17]. Но эти попытки до сих пор ограничены очень простыми классами осцилляторов, эквивалентных фазовым осцилляторам, в основном потому, что это единственный класс осцилляторов, которые могут быть аналитически изучены и для которых сходимость может быть доказана при добавлении адаптивности системы. Для адаптивных релаксационных осцилляторов также разработана модель восприятия ритма [8]. Эти осцилляторы способны адаптировать их частоты для синхронизации с внешним входом. Но эти входные сигналы просты и сводятся к периодической последовательности импульсов.

      Недавно был разработан адаптивный осциллятор для изучения адаптивного передвижения в биоподобных роботах [3,4]. В этой работе разработана адаптивная частота осциллятора Хопфа в состоянии приспособленности к резонансной частоте механической системы. Осциллятора в состоянии адаптировать свою частоту к частоте комплекса входных сигналов. В данной статье доказывается сходимость этого осциллятора и обобщаются адаптивные правила для более сложных осцилляторов, чтобы они могли распознавать частоты и синхронизировать в какой-либо ритмический входной сигнал. Интересной особенностью нашего метода является то, что мы не останавливаемся на фазовой синхронизации колебаний. Добавим пластичность системы, в том смысле, что система может изменять собственные параметры для того, чтобы распознать частоты периодических входных сигналов. Таким образом,  диапазон частот, которые можно извлечь, не ограничен и, распознав, осциллятор продолжает колебаться на распознанной частоте, даже если входной сигнал исчезает. Мы называем наш адаптивный механизм динамическим обучением Хебба, потому что он разделяет сходство с корреляционно-ориентированным обучением, наблюдаемым в нейронных сетях [11].

       Одним из главных аспектов нашего подхода является то, что осциллятор распознает частоты с любого периодического входа, без какой-либо обработки сигналов. Это означает, что осциллятор может адаптировать свои частоты на любой периодический или даже псевдо-периодический вход. Процесс полностью динамический, и не требует образца временного окна или аналогичных переменных параметров, как это часто бывает в обработке сигналов рабочих алгоритмов. Весь процесс обучения и извлечения входной частоты полностью встроен в динамику системы. Другой интересной особенностью метода является то, что мы можем непосредственно применить его на многие другие виды осцилляторов, например, релаксационные или неизученные аттракторы. Осциллятор, на который действует возмущение периодического сигнала F, описывается общими уравнениями:

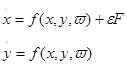
где ω – некоторый параметр, влияющий на частоту колебаний. Введем правило обучения для этого параметра

_.

Знак зависит от направления вращения предельный цикл в фазовом пространстве (х, у) . Это общее правило адаптации работает для многих различных осцилляторов, ω будет сходиться к значению одной частоты компонента осциллятора и одного входа из функции F. Мы обсудим это общее правило обучения в этой статье.

      В разделе 2, мы сначала представим адаптивные правила обучения с простым осциллятором Хопфа и докажем сходимость и устойчивость всей системы. Затем, в разделе 3, мы представим некоторые численные эксперименты, чтобы показать, что осциллятор может адаптировать свои частоты на частоту любого вида периодических или псевдо-периодических сигналов. Наконец, для того, чтобы продемонстрировать общность наших

методов, мы  построим в разделе 4, адаптивный осциллятор  Ван дер Поля, который мы обсудим в деталях. Мы также приведем примеры частотной адаптации с адаптивными осцилляторами Рэлея,  Фитцхью-Нагумо и адаптивной системой Росслера. В разделе 5 мы подведем итоги и подискутируем.

      2 ЧАСТОТНОЕ ОБУЧЕНИЕ ОСЦИЛЛЯТОРА ХОПФА

      В этом разделе мы введем правило обучения для частотной адаптации в осцилляторах. Чтобы сохранить обсуждение как можно более простым, мы используем осциллятор Хопфа, чтобы обсудить наш метод обучения, потому что его фазу эволюции описать просто. Обобщения для более сложных осцилляторов будут представлены в дальнейших разделах. Сначала мы представим модель, а затем мы докажем сходимость адаптивной динамической системы.

      2.1 Описание модели

      2.1.1 Осциллятор Хопфа

      Динамика осциллятора Хопфа описывается следующими дифференциальными уравнениями:

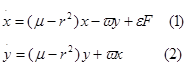
где , μ > 0 контролирует амплитуду  колебаний, а ω является собственной частотой осциллятора. Это означает, что без возмущений (при ε = 0), система совершает колебания ω рад·с^-1. Этот осциллятор связан с периодической силой F. Когда сила равна нулю, система имеет асимптотически стабильный гармонический предельный цикл с радиусом   и частотой ω. Так как предельный цикл осциллятора Хопфа является устойчивым, малые возмущения вокруг предельного цикла (> 0) не меняют общего поведения системы. Это означает, что предельный цикл будет по-прежнему существовать, только его форма и длительность будут меняться. Структурная устойчивость обеспечивает небольшое изменение.

      Если быть заинтересованным в динамической фазе, то систему уравнений (1)(2) переписывают в полярных координатах. Полагают, что x=rcosφ, y=sinφ. Получают:     

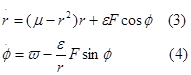
      Хорошо известно, что, когда осциллятор имеет свою собственную частоту ω близкую к частоте компонента периодического входа, это называется этапом фазовой синхронизации. Это означает, что колебания синхронизируются с частотой периодического входа. Максимальное различие между собственной частотой осциллятора и периодическим входом по-прежнему позволяет фазовой синхронизации напрямую зависеть от силы связи. Чем больше различие, тем сильнее связь. Вне этого расстояния осциллятор все еще находится под влиянием связи, но синхронизации уже нет. Если периодический вход имеет несколько частотных компонентов, затем появляются несколько различий. Фазовая синхронизация можно будет возможна с каждой частотой компонента. За пределами расстояния, осциллятор будет иметь тенденцию к ускорению или замедлению, в зависимости от Fsinφ, в среднем генератор будет иметь тенденцию совершать колебания с частотой, которая находится в промежутке между собственной частотой осциллятора и частотой входа. В случае многочастотных входов, эти колебания будут влиять

в подобной манере.

 

      2.1.2 Адаптация динамической системы

     

      Теперь мы можем построить наше правило, используя влияние внешнего возмущения на активность осциллятора. Правило адаптации для динамической системы будет иметь вид:                      

      В дальнейшем мы мотивируемся конкретным выбором правила адаптации, рассуждая о действиях возмущения в геометрическом пути в фазовом пространстве динамической системы. Это дает представление о нашем выборе правила обучения. В дальнейших разделах мы покажем более строго, что это предположение является подходящим и приводит к желаемому поведению.

      Чтобы получить хорошее представление о действиях возмущений в предельном цикле системы (т.е. осциллятор) было бы полезно взглянуть на предельный цикл в представленном фазовом пространстве. В фазовом пространстве все возмущения имеют направление, т.е. они могут быть представлены в виде вектора    в этом пространстве.

      Из-за свойств устойчивости предельного цикла системы возмущение может  долгий срок  действовать только в фазе осциллятора. Фаза незначительно стабильна, тогда как система затухает перпендикулярно предельному циклу. Это означает, что фазовая точка всегда возвращается к предельному циклу, но она может быть сдвинута по фазе. Другими словами, система после сингулярного возмущения будет забывать влияние всех возмущений, кроме возмущения по фазе.

      Особенно в малой окрестности предельного цикла малого возмущения можно сильно действовать в фазе, если оно возмущает осциллятор в направлении касательной к предельному циклу. Возмущения, перпендикулярные  пределу цикла, затухают. Область, где это предположение справедливо, зависит от связь фазы и радиуса. Хотя для осциллятора Хопфа это предположение действует в течение очень большой области, область может быть очень малой для других осцилляторов, например, осцилляторов с сильно согнутыми изохронами.

     Чтобы обсудить влияние возмущения на фазу в этой окрестности, введем систему координат с началом в точке фазы. Первый основной вектор

выбирается перпендикулярно пределу цикла, а второй основной вектор   выбирается по касательной к пределу циклу (рис. 1). Таким образом, эта система координат вращается с фазой точки вдоль предельного цикла. Зная влияние  возмущения в фазе это является достаточным для проектирования  на :

      Таким образом, в зависимости от внешних возмущений и состояния осциллятора (то есть положения точки на предельном цикле) возмущение ускоряет фазу точки или замедляет ее. Если возмущение является периодическим сигналом, в результате получают среднее ускорение или замедление в зависимости от различных частот. Этот эффект, если частота осциллятора и внешняя частота близки, приводит к хорошо известной фазовой синхронизации поведения. Таким образом, влияние несет информацию, необходимую для адаптации к частоте внешнего возмущения. Следовательно, если взять тот же эффект для настройки частоты осциллятора (на медленной шкале времени), частота должна эволюционировать в сторону частоты возмущения. Таким образом, эффект от F (ω, r, φ, F) на ω должен быть таким же, как влияние возмущения на фазу, таким образом, (в среднем) перемещение ω в направлении частоты возмущения.

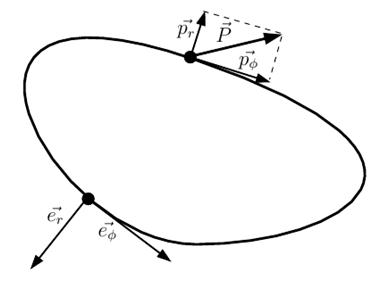
Рисунок 1 – Система координат, где синхронизация наиболее естественная

Рис. 1 показывает произвольный предельный цикл. Система сильно затухает в направлении, перпендикулярном предельному циклу  и незначительно стабильна в направлении касательной к предельному циклу. Это является причиной для структурно устойчивого предельного цикла в первой плоскости и позволяет сброс фазы на других. Обратите внимание, что в двумерном представлении всегда имеет место для обсуждения предельный цикл, так как существует всегда двумерное многообразие, которое содержит предельный цикл. См. текст, касающийся возмущения .

      Хотя обсуждение здесь действует в течение предельных циклов в любой форме и в любом измерении, в случае осциллятора Хопфа и возмущения выбираются по уравнениям (3) и (4), очевидно, что .  Мы выбираем соответственно

Это соответствует картезианской системе координат

      Адаптация ω происходит в более медленном масштабе времени, чем эволюция остальной части системы. Эта шкала адаптации времени повлияла на выбор ε. Обратите внимание, что переменная r удаляется, поскольку мы не хотим использовать правило обучения, которое масштабируется по амплитуде колебаний. С этим правилом, осциллятор будет адаптироваться к любой частоте входного сигнала. Как приложения большинства сигналов будут негармоническими, то есть они имеют несколько частотных компонентов, осциллятор будет адаптироваться к одному из этих компонентов, как правило, ближе всего к собственной частоте осциллятора. Мы должны также отметить, что требуется сохранить осциллятор в сочетании с входом, потому что это эволюция , то есть изменение частоты коррелирует с ω, что дает возможность адаптации в уравнении (7). Доказательство сходимости этого адаптивного осциллятора (уравнения (3), (4) и (7)) в общем случае многочастотных входов приведено в следующем разделе.