| УДК 621.313.333.001.57 | В.С. Петрушин, канд. техн. наук, А.А. Таньков |
ЭНЕРГЕТИЧЕСКИЕ ПОКАЗАТЕЛИ АСИНХРОННОГО ДВИГАТЕЛЯ В ЧАСТОТНОМ ЭЛЕКТРОПРИВОДЕ ПРИ РАЗЛИЧНЫХ ЗАКОНАХ УПРАВЛЕНИЯ |
|
|
Виведено математичні залежності ККД та коефіцієнту потужності асинхронного двигуна від коефіцієнтів зміни частоті та напруги, ковзання, та параметрів заступної схеми при різних законах частотного керування. За ними розраховані енергетичні показники конкретного двигуна. |
Широкое применение во многих отраслях народного хозяйства находят регулируемые частотные асинхронные электроприводы. Наиболее распространенными из них являются приводы с полупроводниковыми преобразователями частоты (ППЧ), использующими автономные инверторы напряжения (АИН). Для обеспечения требуемых характеристик двигателя и получения высоких энергетических показателей одновременно с изменением частоты необходимо менять и величину питающего напряжения по определенному закону. Законы частотного управления можно разделить на две группы. К первой группе относятся законы, связывающие величины и частоты питающего двигатель напряжения (U/f=const, U/f 2=const, U/ =const и другие). Ко второй - законы, обеспечивающие постоянство различных магнитных потокосцеплений электрической машины: статора ?1 (соответствующее постоянству Евнеш /f), воздушного зазора ?0 (постоянству Е/f ), ротора ?2 (постоянству Евнут/f). Особенно распространен последний закон, называемый также векторным управлением. С его помощью обеспечивается непосредственное управление моментом электродвигателя. При этом качество управления электроприводом в статических и динамических режимах существенно повышается по сравнению с другими законами). |
|
Выведены математические зависимости КПД и коэффициента мощности асинхронного двигателя от коэффициентов изменения частоты и напряжения, скольжения и параметров схемы замещения при разных законах частотного управления. По ним рассчитаны энергетические показатели конкретного двигателя. |
|
|
The mathematical dependencies of cage induction motor efficiency and power factor from factors of frequency and voltage change, rotor slip and parameters of equivalent circuit for the different laws of a frequency control are deduced. The power indexes of the specific induction motor are calculated. | |
В данной статье рассматриваемые энергетические показатели представляются в виде математических зависимостей от коэффициентов изменения частоты и напряжения, скольжения и параметров схемы замещения двигателя. Эти математические зависимости можно получить, анализируя эквивалентную схему замещения двигателя (рис.1). В ней все сопротивления, исключая активные сопротивления обмотки статора r1 и обмотки ротора r2' , изменяются пропорционально параметру a = f1 / f1н , представляющему собой отношение текущей и номинальной частот двигателя. Приведенное активное сопротивление обмотки ротора r2' обратно пропорционально абсолютному скольжению, равному отношению частоты ротора к номинальной частоте двигателя b = f2/f1н = as, где s скольжение двигателя. Приложенное к двигателю напряжение будем оценивать величиной g = U1 / UN - отношением текущего и номинального напряжений двигателя. При рассмотрении энергетических показателей для более точного определения потерь в стали целесообразно не исключать из эквивалентной схемы сопротивление r0
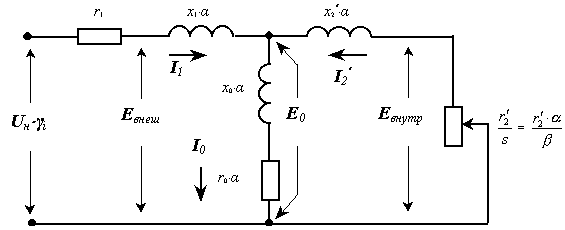
Рисунок 1 - Эквивалентная схема замещения асинхронного двигателя
Взаимосвязанное управление напряжением и частотой преобразователя при законах первой группы определяются следующими соотношениями: g =a при U/f = const, g =a2 при U/f2 = const и т. д. [1].
Для удобства записи используем следующие коэффициенты, характеризующие соотношение индуктивных (цепи намагничивания х0, рассеяния статора х1, рассеяния ротора х2') и активных сопротивлений:
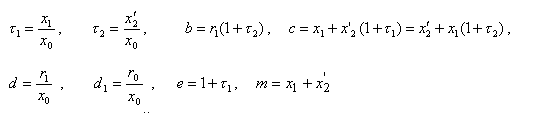
В соответствии со схемой замещения токи двигателя при законах частотного управления первой группы определяются выражениями:
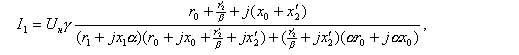
или используя предложенные выше коэффициенты:
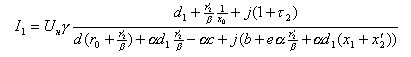
Аналогично находятся другие токи:
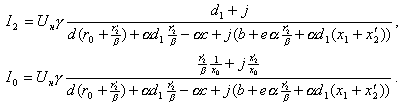
После преобразований выражения для эффективных значений токов приобретают следующий вид:
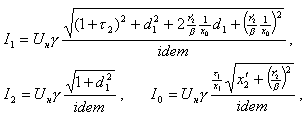
где
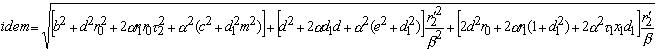
Используя выражения для первичного тока и его активной составляющей, определяем коэффициент мощности cosj1= I1a/I1:
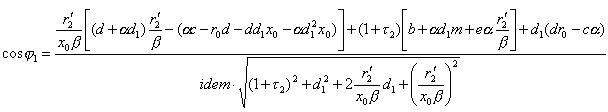
Приведенные выражения для токов позволяют определить потери и коэффициент полезного действия.
Электрические потери в обмотке статора:
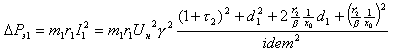
Электрические потери в обмотке ротора:
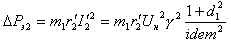
Потери в стали:
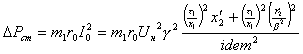
Добавочные потери:
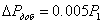
Принято, что механические потери двигателя изменяются пропорционально угловой скорости ротора в степени 3/2 [1]:
DPмек=a3/2Pтрн
где Pтрн - механические потери при номинальной нагрузке.
Коэффициент полезного действия:
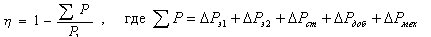
После некоторых преобразований получаем:
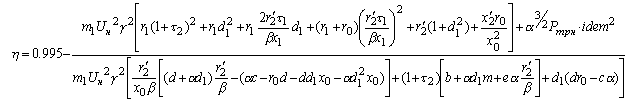
Как было отмечено выше, законы управления второй группы характеризуются постоянством ЭДС. Получение выражений энергетических показателей для различных законов второй группы поясняется с помощью схемы замещения (рис. 1). Рассмотрим случай регулирования постоянства потокосцепления статора Y1 , т.е. поддержания постоянства Евнеш/f. При таком регулировании выражение тока статора принимает вид:
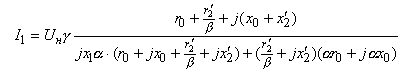
Тогда на входе схемы напряжение Uвх должно быть больше рассматриваемой ЭДС на величину падения напряжения на активном сопротивлении статора
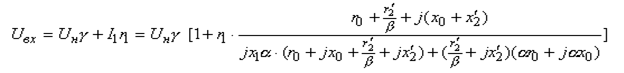
Для определения этого увеличения введем коэффициент
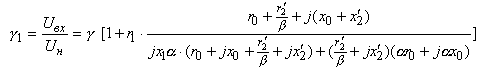
В последующем используется абсолютное значение этого коэффициента
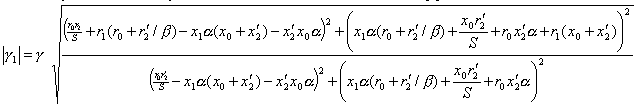
Аналогично выводятся выражения коэффициентов g2 и g3 при других законах частотного управления второй группы, в том числе и для векторного управления (g3).
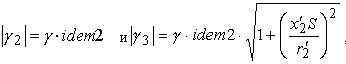
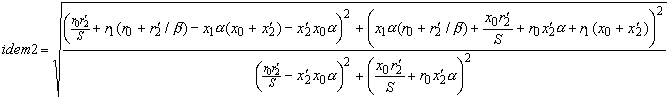
Подставляя найденные коэффициенты gi вместо g в выражения для h, получаем выражения КПД при различных законах частотного управления.
Полученные выражения h и cosj2 позволяют произвести расчеты этих энергетических показателей. Параметры схемы замещения, входящие в состав этих выражений, должны определятся в каждой рабочей точке с учетом влияния насыщения магнитопровода и вытеснения токов в обмотках.
Были проведены теоретические исследования энергетических показателей асинхронного двигателя АМУ160L2У3 (Рн=18,5 кВт) при различных законах частотного управления, результаты которых представлены на рис.2. Там же даны результаты эксперимента, проведенного при испытании этого двигателя (закон частотного управления U/f = const). Двигатель работал на нагрузку с постоянным моментом 30,5 Нм в диапазоне скоростей 500 - 2930 об/мин.
Сопоставляя полученные зависимости можно сделать вывод, что в зоне небольших скоростей при использовании законов управления второй группы КПД больше на 7-21%, а коэффициент мощности меньше на 3-7%. С увеличением скорости различия снижаются.
Таким образом, законы второй группы обеспечивают не только лучшее управление электроприводом в статических и динамических режимах, но и повышение КПД двигателя и, соответственно, всего привода.
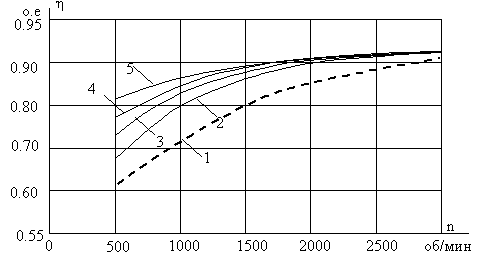
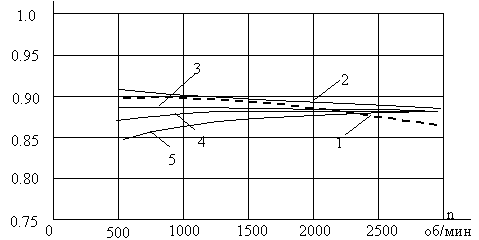
Рисунок 2 - Изменение КПД h (а) и cosj1 (б) в диапазоне регулирования: 1 - экспериментальные зависимости; расчетные зависимости при разных законах управления: 2 - U/f = const, 3 - Евнеш /f = const, 4 - Е/f= const, 5 - Евнут /f= const.
Список использованной литературы
1. Булгаков А.А. Частотное управление асинхронными электроприводами. - М.: Энер-гоиздат . 1982. - 216 с.