Выбор оптимального режима контактной точечной сварки методом планирования эксперимента

 

Авторы: В.Г. Квачев

Источник: журнал «Автоматическая сварка» – 1971 г., №2, – С. 20-23

 

Контактная точечная сварка — один из самых производительных способов соединения металлов. В связи с широким использованием ее в массовом производстве и отсутствием совершенных методов неразрушающего контроля особое значение приобретает строгое соблюдение требований, предъявляемых к технологическому процессу на этапах подбора режима, подготовки материалов под сварку, сборки деталей и т.д. При этом подбор оптимального режима сварки определяет воспроизводимость заданного качества соединений. Нетрудно показать, что при прочих равных условиях и постоянной колеблемости основных параметров режима функция стабильности качества y=f(x_1, x_2…x_n) — параметры режима, зависит от соотношения этих параметров и имеет максимум в области оптимальных режимов сварки.

При точечной сварке материала определенной толщины режим задается временными зависимостями сварочного тока I_св(t) и усилия сжатия F_cж(t), а также размерами и формой контактной поверхности электродов.

Рядом исследователей предложены формулы для расчета тока, как основного параметра, обусловливающего выделение тепла при сварке [1, 2]. Однако попытки их практического использования сопряжены с известными трудностями, вызванными сложностью расчетов и несовпадением полученных данных с практическими результатами [3]. В последнее время для определения режимов сварки применяют теорию подобия или метод обобщенных переменных [4].

Однако существующие аналитические методы позволяют лишь предварительно оценить область изменения параметров режима, окончательный выбор которых требует существенного экспериментального корректирования.

Результаты корректирования расчетных и табличных значений параметров практически всецело зависят от квалификации технолога- сварщика, его опыта и методики, используемой при подборе режима. Естественно, такой подход привносит субъективный фактор, что зачастую приводит к непроизводительным затратам времени и материалов.

Выбор и корректирование режимов сварки — типичная задача оптимизации, т.е. нахождения наилучших в определенном смысле значений параметров режима. При заданном критерии качества (обычно это диаметр ядра (d_я или разрывное усилие) задача оптимизации заключается в определении параметров, принадлежащих некоторой области допустимых значений и обеспечивающих экстремум выбранного критерия.

При наличии аналитической зависимости между управляющими параметрами режима и критерием качества решение этой задачи не составляет особого труда. Однако недостаточная изученность процесса сварки, большое количество параметров и случайный характер возмущений не позволяют получить достаточно точного аналитического описания. Поэтому оптимальные параметры режима могут быть определены с помощью методов математического планирования экспериментов, основанных на обработке данных, которые получены непосредственно на действующем объекте. При этом в отличие от аналитического исследования осуществляется локальное изучение поверхности отклика [5] по результатам некоторого набора экспериментов, В результате ряда последовательных процедур изучения поверхности отклика получают его экстремальное значение, причем эксперименты планируются таким образом, чтобы минимизировать количество опытов и время, затрачиваемое на поиск экстремума. Обычно наиболее эффективно использование факторных методов планирования, получивших в последнее время широкое распространение при исследовании технологических процессов.

Для решения поставленной задачи был применен метод последовательного симплекс-планирования [5, 7]. Основная идея его заключается в том, что поверхность отклика в некоторой области аппроксимируется линейным приближением с помощью минимального числа экспериментальных точек, образующих симплекс, и движение по этой поверхности в поисках оптимального значения осуществляется путем отбрасывания вершины симплекса с меньшим откликом и построения новой, являющейся зеркальным отображением отброшенной. Это позволяет совместить процесс изучения поверхности отклика с перемещением по ней. Достигнув области экстремума, симплекс начинает вращение вокруг вершины максимальным откликом. Это свидетельствует о том, что все остальные вершины, определяемые соотношением исходных параметров, дают меньший по сравнению с дентальной выход и используются для определения окончания процесса оптимизации.

Более подробное описание алгоритма метода симплекс-планирования будет рассмотрено ниже. Здесь же необходимо отметить основные достоинства, обусловившие выбор этого метода для решения задачи:

1) использование его не требует специальных математических знаний. Вычисления крайне просты, все приемы формализованы, поэтому метод пригоден как для ручной, так для машинной реализации;

2) направление движения определяется не точными количественными значениями отклика, а лишь соотношением между ними. Это особенно важно в случае затруднений при измерении показателя качества сварки;

3) ввиду того, что перемещение симплекса основывается на качественной информации не нужно предъявлять слишком высокие требования к точности поддержания и измерения значений параметров, соответствующих координатам вершин. Это позволяет использовать метод непосредственно в производственных условиях, где измерение и поддержание значений параметров с высокой точностью затруднены.

Ниже на примере выбора оптимального режима точечной сварки материала Д16АМ  мм на низкочастотной машине показана методика применения симплекс-планирования. Эксперимент планировался для двух независимых переменных режима: максимального значения импульса сварочного тока I_{св max} и усилия сжатия электродов F_сж. Остальные параметры (время сварки, диаметр электрода d_э радиус его заточки R_з и т.д.) поддерживались на заданном уровне.

На основании данных таблиц рекомендованных режимов выбирались диапазон изменения каждой из переменных: 25 кА I_{св max} 35 кА, 280 кг_сж400 кг – интервал варьирования ; величина  кА,  кг.

В качестве критерия оптимизации принимали диаметр ядра сварной точки. Переменные режима измерялись с помощью специализированной аппаратуры [6].

Симплексом, как известно, называется простейшая выпуклая геометрическая фигура, обладающая минимальным количеством вершин n+1, где n - число исследуемых переменных. В рассматриваемом случае при n=2 регулярный симплекс представляет собой равносторонний треугольник, координаты вершин которого в пространстве исследуемых переменных определяют план опытов.

Начальный симплекс строился для режима I_{св max}=175. F_сж=120. Ввиду того что предварительная оценка направления движения затруднена, ориентация первоначального симплекса произвольна. Поэтому расположим его сторону А₁–А2 параллельно оси тока (рисунок, а). Учитывая выбранные интервалы варьирования параметров и пользуясь матрицей планирования [7], строим начальный симплекс A₁A₂A₃. Результаты опытов в вершинах симплекса (табл. 1) показали, что минимальное значение диаметра ядра дает режим, определяемый точкой А₂. Поэтому для осуществления движения в направлении увеличения отклика необходимо отбросить точку А₂ и на оставшейся стороне А₁–А₃ достроить новый симплекс путем добавления точки А₄.

Координаты новой точки определяются следующим соотношением:

 

A_ji=2/n(A_1i + A_2i + …+ A_ji + …+ A_k+1.i) - A_ji

 

i=1, 2, 3,…, k.

 

Здесь первый индекс обозначает номер вершины симплекса, а второй — ее координату: j - номер вершины с минимальным откликом. Для рассматриваемого случая координаты точки А₄вычисляются так:

 

A₄(F_сж)=2/2 [A₁(F_сж)+A₃(F_сж)]–A₂(F_сж);

 

A₄(I_св max)=2/2[A₁(I_св max)+A₃(I_св max)]–A₂(I_св max).

 

После проведения эксперимента в точке A₄ производится сравнительная оценка диаметра ядра для режимов A₁, A₃, A₄ . Точка симплекса с минимальным выходом отбрасывается и описанная процедура повторяется.

 

 

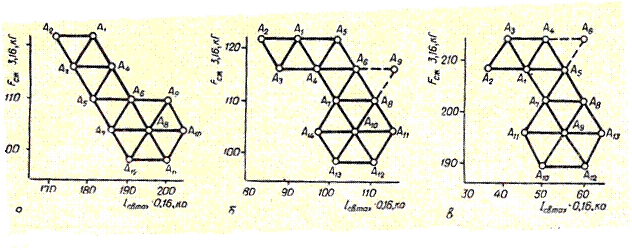
Рис. 1 – Траектория движения симплекса при определении оптимального режима сварки (d_э=20мм, R_з=75мм)

А - сплава Д16АМ; б – сплава АМг6; в – нержавеющей стали 1Х18Н9Т

 

Как видно из рисунка 1 и табл. 1, после достижения симплексом точки А₈ поступательное движение прекратилось.

 

Таблица 1

 

 

При сварке на режиме, определяемом точкой А₁₀, диаметр ядра увеличился, но при этом произошел выплеск. Следующий симплекс был построен на стороне А₈…А₁₀, и эксперимент, проведенный в точке А₁₁, также привел к выплеску. Завершающий опыт в вершине А₁₂ дал существенно меньшие размеры диаметра ядра по сравнению с режимом, определяемым точкой А₈.

После завершения цикла вращения симплекса вокруг вершины А₈ оказалось, что режимы A₉,A₁₀, A₁₁, A₁₂ дают меньший диаметр ядра либо приводят к выплескам.

Для уточнения координат оптимального режима в точке А₈ был проведен ряд опытов, которые дали хорошую воспроизводимость результатов. Таким образом, в качестве оптимального был определен режим, соответствующий вершине А₈ с координатами I_{св max}=190, F_сж=104.

Аналогичный эксперимент по выбору оптимального режима сварки был проведен также для материалов АМг6 и 1Х18Н9Т  мм. Траектории движения симплексов для них приведены на рис. б и в. В табл. 2 указаны оптимальные режимы в натуральных единицах.

 

Таблица 2

 

 

Литература:

 

1. А.С. Гельман, Технология и оборудование контактной сварки, Машгиз, М., 1960.

2. К.А. Кочергин, Вопросы теории контактной сварки, Машгиз, М, — Л., 1950.

2. Г.Ф. Скакун, А.А. Чакалаев, К вопросу расчета некоторых параметров режима точечной сварки легких сплавов, сб. «Надежность сварных соединений и конструкций», «Машиностроение», М, 1967.

3. В.К. Лебедев, Ю.Д. Яворский, Применение критериев подобия для определения режимов сварки, «Автоматическая сварка», № 8, 1960.

4. В.В. Налимов, Н.А. Чернова, Статистические методы планирования экстремальных экспериментов, «Наука», М., 1965.

5. Б.Е. Патон и др., Автоматизация экспериментальных исследований сварочных процессов, «Автоматическая сварка», № 6, 1970.

6. П.В. Ермуратский, Симплексный метод оптимизации, «Труды МЭИ», вып. 67, 1966.