Седьмая международная конференция в CFD по обрабатывающей промышленности CSIRO, Мельбурн, 9-11-2009 декабря

ХАРАКТЕРИСТИКА ВИНТОВОГО (СПИРАЛЬНОГО) КОНВЕЙЕРА: СРАВНЕНИЕ ДИСКРЕТНОГО МОДЕЛИРОВАНИЯ С ЛАБОРАТОРНЫМИ ЭКСПЕРИМЕНТАМИ

Филипп J. ОУЭН и W. CLEARY

Перевод: Бабич Станислав

Винтовые конвейеры широко используются в сельском хозяйстве и перерабатывающей промышленности для подъема и транспортировки насыпных материалов на средние расстояниям. Они очень эффективны для передачи сухих сыпучих тел, подвергаясь хорошему контролю. Несмотря на их очевидную простоту действия, их конструкция очень сложна. В нашей предыдущей работе, мы исследовали, как характеристики винтового конвейера воздействуют на его рабочие режимы (как например: ротационная скорость винта, наклонного винтового конвейера, и его объемного уровня достаточного количества ). В этой работе, рассматривается, что норма массового потока отлично сочетается с экспериментально взвешенными значениями для горизонтальных и вертикальных конфигураций через полную амплитуду норм винтового вращения. Хотя прогнозы производительности для винтового конвейера с углом наклона в 30° и 60° следовали за той же качественной тенденцией, были умеренные отличия между DEM и экспериментальными исходами. В этой статье, мы используем Дискретный Метод (ДЕМОДУЛЯТОР), чтобы исследовать, как вариации свойств частицы влияет на характеристику винтового конвейера. Первичным центром нашего изучения, было сравнение нормы массового потока с экспериментально взвешенными значениями. Вторичным центр - научиться, как другие критерии (как например: скорости частицы и энергетическое потребление) качества работы изменяются благодаря изменениям в свойствах частиц.

ВВЕДЕНИЕ

Винтовые конвейеры широко использованы для транспортировки и подъема частиц в управляемых и установившихся нормах. Они использованы во многих приложениях насыпных материалов в промышленности, очистке от индустриальных минералов, сельского хозяйства (грануляции), фармацевтической продукции, химикалиев, пигментов, пластмасс, цемента, песка, соли и переработки продуктов питания.

Краткий отчет текущих методов проекта и задач и опытов для винтовых конвейеров, содержутся в Bortolamasi и Fottner (2001).

Описание теоретического поведения винтовых конвейеров рассмотрено в статьях Yu и Арнольд (1997), и Roberts (1999).

ДЕМОДУЛЯТОР, моделирующий сыпучего потока в винтовом конвейере был впервые сообщен Shimizu и Cundall (2001). Они исследовали характеристику горизонтальных и вертикальных винтовых конвейеров и сравнили их исходы с предыдущими рабочими и эмпирическими выравниваниями. Оуэн и другие. (2003)

введено использование периодического моделирования, чтобы исследовать характеристику длинного винтового конвейера. Cleary (2004)

ДЕМОДУЛЯТОР используется, чтобы определить максимально близкое расстояние образца от прыгуна при угле наклона винтового конвейера 45°. Эту работу расширил Cleary (2007), чтобы исследовать эффект формы частицы на тяге внизу от прыгуна и на транспортных характеристиках винтового конвейера.

ДЕМОДУЛЯТОР ОБРАЗЦОВОГО ОПИСАНИЯ

Моделирование завертывает следование движения каждой частицы и каждой коллизии: закрепить частицы в их окружении (например внутренняя поверхность винтового кожуха и поверхность вращающегося винта). Пограничная геометрия построена, используя пакет CAD и импортируя его как треугольное внешнее отверстие в пакете DEM. Это даёт неограниченную гибкость в определении трех имеющих измерениях геометри интермедии частиц. Здесь частицы моделируются как сферы и сверхпрочные квадрики.

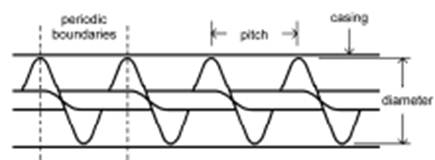
Рисунок 1: винт конвейера одиночного полета.

Винтовой конвейер, использованный в этом изучении, был стандартным, шаг винтового конвейера одиночного полета был, подобными тому который использовали Roberts и Уиллис (1962) в их экспериментах. Шаг винтового конвейера определили, как длина, вдоль приводного вала, из одной очереди спирального лезвия, как показано на Рисунке 1. Стандартный винт имеет свой шаг, равный внешнему диаметру спирального лезвия.

DEM метод упростил применение периодических пограничных условий к единственному шагу винта, как показано на Рисунке 1. Диаметр и шаг винта составили 38 mm, диаметр винта составил 13 mm, и толщина лезвия составила приблизительно 1 mm. Толщина лезвия для винта в экспериментах была около 3 mm (винт был подвергнут механической обработке от твердого бара латуни). Внутренний диаметр для трубчатого случая составил 40 mm, давая брешь около 1mm между внешним лезвием винта и внутренней поверхностью кожуха.

Roberts и Уиллис (1962) использовал Японское просяное семя (грануляция, которая очень близко к сферическому в форме) для сухих частиц в их экспериментах. Размер сферических и не сферических (сверхпрочных квадриков) частиц использовались с 2 mm до 3.6 mm. Их размеры однородно распространялись на массе нагрузил базиса, и все остальной имели плотность 700 кг/м.Базовый случай, составили 0.7 и 0.5, соответственно, и коэффициенты возвращения составили 0.1 и 0.3, соответственно; одни и те же значения, использованные в предыдущем изучении. Обычно, средние перекрытия 0.1–0.5% желательны для этого вида моделирования.

ДЕМОДУЛЯТОР

Ряд моделирований осуществлялся для различных форм частицы, и для амплитуды частиц трений.Во всех моделяхя использовали те же рабочие режимы, а именно: ротационная скорость 1000 оборота в минуту, 30% объемного уровня достаточного количества, и уклон винтового конвейера был различен от 0° к 90° в шагах 30°.

Традиционно частицы ДЕМОДУЛЯТОРА моделируются как сферы в трех измерениях. Здесь мы также используем сверхпрочные квадрики, с общей формой: чтобы описать не сферические частицы. Энергетический N - фактор формы, который определяет частицы (с формой, изменяясь от сферы к кубу как увеличения N). B и C - коэффициенты сжатия.Размер частицы использовал в предыдущем изучении, Оуэне и Cleary (2009),он был основан на типичном размере проса, а именно, 2-3 mm сферические частицы. Некоторые из этих моделирований ДЕМОДУЛЯТОРА были повторными (посмотрите Таблицу 1). В этом изучении мы сократили высший размер частиц к 2.5 mm, чтобы соответствовать Японскому просяному семени, использованному в экспериментах. Для случаев, где частицы были использованы, их размер был взвешен двумя путями. В SQA эксплуатируемые частицы были созданы таким образом, что их размер в их первом незначительном направлении оси был в пределах точно установленной амплитуды размера. Это приводило к слегка более длинным частицам, чем сферы использовали в пробегах SPB . Меньшие частицы были использованы для того, чтобы сохранить, 30% заполняемость уровеня. В оставшихся пробегах частицы были сконструированы таким образом, что их размер в большой оси направление было в пределах точно установленной амплитуды размера. Как последствие, эти частицы были более маленькими и больше частицах были нужны, чтобы получить, 30% заполняемость уровня.

Таблица 1: Свойства частицы - параметры формы.

Формы Частицы ДЕМОДУЛЯТОРА	Размер (mm)	Фактор формы	Коэффициент Сжатия
Сферические частицы	2 - 3	2	1
частицы имеющими более маленький размер.	2 – 2,5	2	1
сверхпрочные квадрики с размером, взвешенным вдоль первой незначительной оси	2 – 2,5	2,1 – 2,2	0,7 – 0,86
размеры, взвешеваний вдоль большой оси (Базовый Случай)	2 – 2,5	2,1 – 2,2	0,7 – 0,86
частицы которые более удлинены	2 – 2,5	2,1 – 2,2	0,55 – 0,7
Частицы которые более глыбистые	2 – 2,5	3,5 – 4,0	0,55 – 0,7

Таблица 1 и Таблица 2 подводят итог амплитуды формы частицы и амплитуды friction значений, использованных в этом изучении. DEM, моделирующий, дал прогнозы для изменений в screw conveyor характеристике благодаря изменениям в свойствах частицы в терминах вариаций: норма массового потока, скорость частицы, и энергетическое потребление.

Таблица 2: Моделируя условия – случаи Friction.

Коэффициент Сжатия	Трение Частицы	Трение Границы
Частицы сверхпрочные квадрики (Базовый Случай)	0,7	0,50
Трение частицы уменьшенное до 20%	0,54	0,50
Трение частицы уменьшенное до 10%	0,63	0,50
Трение частицы увеличенное до 10%	0,77	0,50
Трение частицы увеличенное до 20%	0,84	0,50
Пограничное трение частицы уменьшенное до 20%	0,70	0,40
Пограничное трение частицы уменьшенное до 10%	0,70	0,45
Пограничное трение Частицы, увеличенное до 10%	0,70	0,55
Пограничное трение Частицы, увеличенное до 20%	0,70	0,60