Автор: В.Г. Гуляев, В.Ф. Сивокобыленко, К.В. Жуков
Источник: Известия ВУЗов, Энергетика, 2006, № 1, с. 43 - 48.
На современном этапе и в будущем целесообразно применение лучших серийных очистных комбайнов (ОК) с повышенными показателями надежности и адаптивности [1]. Одним из основных способов повышения надежности ОК является снижение их динамической нагруженности и, прежде всего, электромеханической подсистемы привода исполнительных органов (ППО). Для выявления закономерностей формирования динамической нагруженности в ППО наряду с экспери-ментальными методами применяется имитационное математическое моделирование. Сотрудниками кафедры «Горные машины» ДонГТУ разработаны адекватные математические модели (ММ) ОК, в основном для исследования «установившихся» рабочих режимов на основе линеаризованных динамических моделей электродвигателя и моделей трансмиссии с линейными характеристиками [2,3].
Для приводных двигателей ОК по ГОСТ 16565-71 за номинальный режим работы принят повторно-кратковременный с частыми пусками (S4 условно) с ПВ 60%, с числом включений до 120 в час при коэффициенте инерции до 2,5. В структуре эксплуатационных спектров нагруженности комбайнов большое значение имеют переходные процессы – при разрушении резцами крепких включений, пусковые режимы и опрокиды двигателей, сопровождающиеся формированием высоких динамических нагрузок в ППО. Поэтому актуальна разработка соответствующей адекватной в главном ММ для изучения динамических процессов в ППО. В данной работе рассматривается формирование имитационной ММ ППО для двухдвигательного комбайна с механически связанными (или не связанными) двигателями
ММ электромеханической системы ППО ОК соответствует расчетной схеме с пятью сосредоточенными массами (рис. 1).
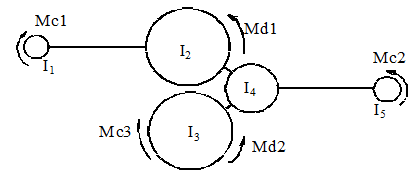
Рисунок 1 – Расчетная схема ППО двухдвигательного комбайна
Сосредоточенные массы соединены упруго-демпфирующими кусочнолинейными связями (рис. 2), что позволяет учитывать возмож-ность «раскрытия» зазоров между элементами трансмиссии.
Рисунок 2 – Характеристика кусочно-линейной связи
На рис. 2 приняты следующие обозначения:
k, n – индексы масс, соответственно, от которой и к которой передается энергия, k,n=1…5; фк,фn-угловые координаты масс k и n; Мkn-упруго-демпфирующий момент на участке kn:
Необходимо отметить, что приравнивание нулю С24 и ?24 позволяет рассматривать режимы работы ОК при механически не связанных двигателях.
Формирование нагрузок в ППО ОК происходит в замкнутой системе «ОК – забой» и носит случайный квазистационарный харак-тер. Наибольшее влияние на этот процесс оказывают неравномер-ность перемещения комбайна, силовая неуравновешенность ИО и сложные автоколебательные процессы в замкнутой системе. С учетом всего этого, моменты сопротивления, приложенные к массам ИО (Мс1 и Мс2) можно представить [2]:
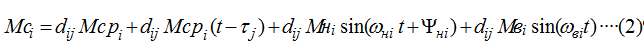
Здесь dij – коэффициент, изменяющий режим нагружения; j – индекс, соответствующий режиму нагружения; dijМсрi(t-тj) – составляющая, необходимая для задания различного темпа нарастания среднего уровня нагрузки; Мсрi, Мнi, Мвi – соответственно средний уровень и амплитуды низ-кочастотных (НЧ) и высокочастотных составляющих нагрузки; Жнi –начальная фаза НЧ составляющих нагрузки; i – индекс, соответствующий номеру ИО (i=1,2).
Момент сопротивления от подсистемы подачи (Мс3) можно предста-вить [2]:
Динамические процессы в двигателях, в т.ч. на нелинейной час-ти механической характеристики, с учетом общеизвестных допуще-ний наиболее полно описывает модель, разработанная на основе фун-даментальных исследований Парка-Горева [4]. Особенностью ком-байновых электродвигателей с глубокопазными роторами является необходимость учета изменения параметров схемы замещения двига-теля в зависимости от скольжения S, что связано с явлением вытесне-ния токов к поверхности стержней. На основе работы [5] произведена замена контура ротора с параметрами Xr и Rr(S) эквивалентным двойным контуром с параметрами Xrв, Xrн и Rrв, Rrн, не зависящими от S. Для учета влияния питающей сети статорные уравнения следует дополнить составляющими падений напряжений, которые в коорди-натной системе a,b,0 с достаточной степенью точности [4] могут быть представлены:
С учетом изложенного выше система дифференциальных урав-нений, описывающая динамические процессы в первом двигателе имеет вид:
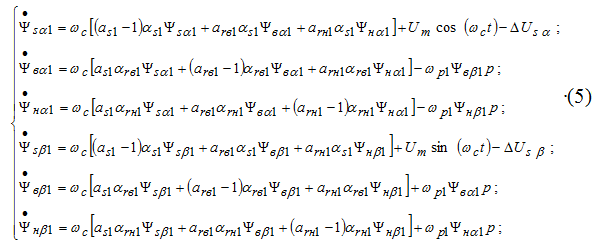
Момент двигателя:
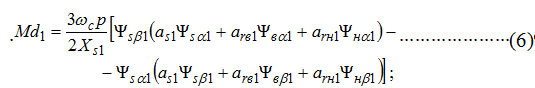
Токи статора в проекции на оси a и b:
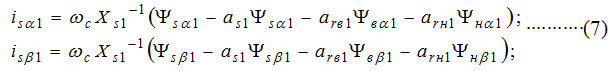
Коэффициенты системы (5) находятся в зависимости от параметров схемы замещения двигателя:
wс=314 рад/с – угловая скорость магнитного поля; p – число пар полюсов; wр1=w2 – угловая скорость ротора первого двигателя (wр2=w3);
Дифференциальные уравнения второго двигателя аналогичны (5)-(8) с учетом замены индекса 1 на 2.
Запишем дифференциальные уравнения движения всех сосредо-точенных масс:
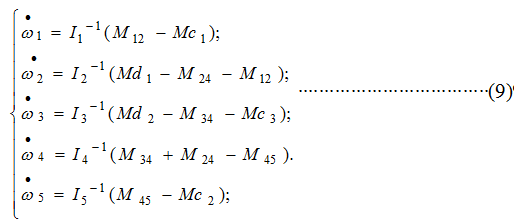
Совместное решение системы уравнений (1)-(9) позволяет определять механические и электромагнитные нагрузки в данной элек-тромеханической системе. При этом в векторе начальных условий общей ММ необходимо учитывать наличие «открытых» случайных по величине зазоров на участках трансмиссии.
С использованием разработанной ММ были исследованы дина-мические режимы ППО комбайна 1ГШ68 с двигателями ЭКВ4УУ5 (110 КВт). Решение уравнений производилось методом Рунге-Кутта с применением ПЭВМ. Некоторые результаты моделирования приве-дены на рис.3,4 .
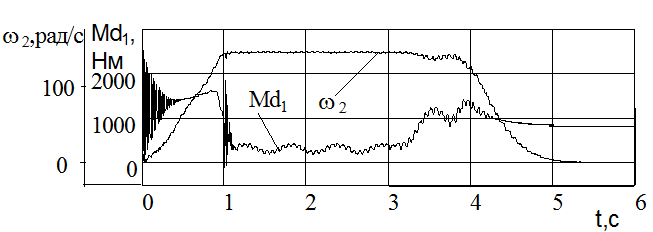
Рисунок 3 – Электромагнитный момент и угловая скорость ротора первого ЭД
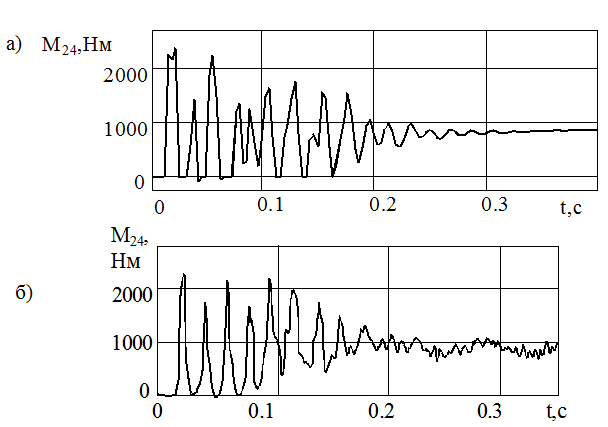
Рисунок 4 - Пуск без нагрузки: а – результат моделирования; б – осцилограмма натурного эксперимента
Полученные результаты подтверждают адекватность разработанной ММ реальному объекту на качественном уровне, однако, необходима дальнейшая ее калибровка. С использованием разработан-ной модели ППО планируется создание ММ замкнутой системы «очистной комбайн – забой» с рассмотренной структурой ППО, а также со связью роторов ЭД посредством электромагнитной муфты скольжения [1].