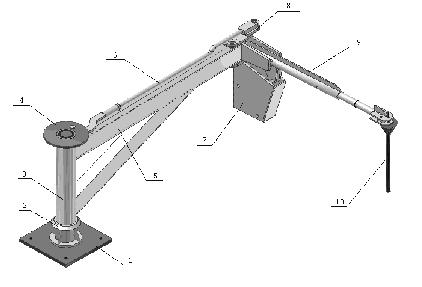
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ И САПР ПРИ РАЗРАБОТКЕ УСТРОЙСТВА ДЛЯ ОТСЕЧКИ КОНВЕРТЕРНОГО ШЛАКА
Автор: С.П. Еронько, Е.В. Ошовская, В.В. Киселев, Ю.Г. Полонская, А.В. Копейко
Источник: http://www.uran.donetsk.ua/~masters/
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ И САПР ПРИ РАЗРАБОТКЕ УСТРОЙСТВА ДЛЯ ОТСЕЧКИ КОНВЕРТЕРНОГО ШЛАКА
The design elaboration of manipulator for converter slag cutting is described in the article. The analytical solution of four link mechanism synthesis problem is given. This mechanism is the main unit of proposed manipulator and provides the assign motion law of pole held cutting element. The 3D solid model of elaborated manipulator is shown. The model is made using the automated design system Autodesk Inventor.
Предотвращение попадания большого количества окислительного шлака в разливочный ковш во время слива стали из кислородного конвертера является важной технологической задачей, от успешного решения которой во многом зависит эффективность мероприятий, связанных с рафинированием металла и его доводкой по химическому составу [1,2].
Для обеспечения бесшлакового выпуска стали из кислородных конвертеров в настоящее время используется несколько технических решений, предпочтительным из которых является вариант отсечки шлака с применением отсечных элементов поплавкового типа, снабженных направляющим стержнем [3-5].
Специфика работы манипуляторов, осуществляющих подачу отсечных элементов внутрь конвертера, обусловлена не только экстремальными условиями их эксплуатации (высокие температуры, значительные нагрузки и запыленность окружающего пространства), но и необходимостью обеспечения высокой точности позиционирования рабочего органа и компактности размещения конструкции в нерабочем положении. Указанные особенности эксплуатации предъявляют высокие требования к конструкции манипулятора, которые должны учитываться на стадии его создания. Вопросы синтеза кинематической схемы механизма, обеспечивающего требуемую точность позиционирования отсечного элемента относительно выпускного канала конвертера, и оптимизации конструктивного исполнения механической системы в целом требуют при решении комплексного подхода. В этом случае для получения исходных данных целесообразно использовать метод математического моделирования и САПР, позволяющих имитировать работу манипулятора в различных режимах и определять нужное соотношение линейных и угловых размеров его структурных элементов.
При разработке конструкции нового манипулятора ставилась задача обеспечения возможности ее складывания, что позволяло бы не создавать помехи работающим на площадке возле конвертера другим машинам, выполняющим работы по ремонту (торкретированию) и ломке отслужившей установленный срок огнеупорной футеровки плавильного агрегата. Главным узлом предлагаемой конструкции манипулятора является двухкоромысловый четырехзвенный механизм (рис.1), обеспечивающий заданный закон движения штанги, несущей отсечной элемент (стопор).

Рис.1. Схема четырехзвенного рычажного механизма манипулятора
1 – коромысло; 2 – шатун; 3 – коромысло; 4 – стойка; 5 – штанга
Задача синтеза данного рычажного механизма в соответствии с классификацией, приведенной в работе [6], состоит в определении длины коромысла c и расположения шарнира С.
Движение шарнира В, принадлежащего шатуну (звено 2), происходит по окружности, описываемой уравнением:
 (1)
(1)
где j – угол поворота коромысла а, j = 0 ... 180o.
При повороте коромысла 1 на 180o шатун 2 должен расположится перпендикулярно ему, при этом точка В переместится в точку Вк, а точка А - в точку Ак. Уравнение окружности, проходящей через точки В и Вк, имеет вид:
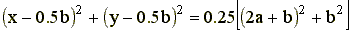 (2)
(2)
Центр окружности – точка S – располагается в середине отрезка ВВк, радиус окружности равен половине отрезка ВВк, R=0,5ВВк.
Чтобы принять точку S в качестве точки поворота коромысла 3 (рис. 1), необходимо проверить отсутствие зазоров (разрывов) между траекториями движения шарнира В по окружностям (1) и (2) при вращении коромысла 1 (рис. 2).
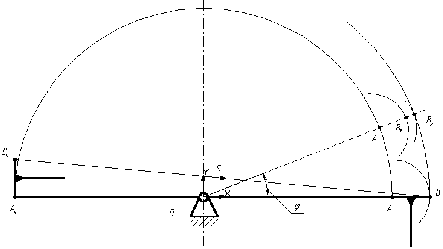
Рис.2 Определение разрыва между траекториями точек
Координаты точки 1 пересечения луча с окружностью (1) находятся как решение системы уравнений и вычисляются по формулам:
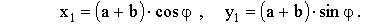 (3)
(3)
Координаты точки 2 пересечения луча с окружностью (2) определяются по выражениям:
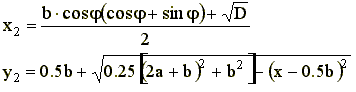 (4)
(4)
где D – дискриминант квадратного уравнения
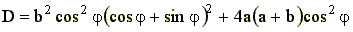
 (5)
(5)
 (6)
(6)
 (7)
(7)
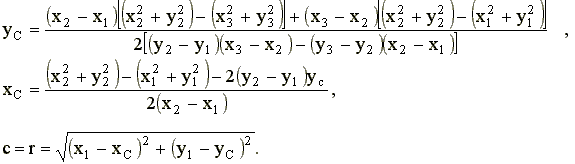 (8)
(8)