Генералов М.Б.

ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПРИ ОДНОСТОРОННЕМ ПРЕССОВАНИИ ЦИЛИНДРИЧЕСКИХ БРИКЕТОВ ИЗ МЕТАЛЛИЧЕСКИХ ПОРОШКОВ

Сборник трудов Московского института химического машиностроения , Москва, 1975г., вып. 65, с 19-27

        Исследование закономерностей распределения давлений и плотностей при прессовании цилиндрических брикетов из металлических порошков.

Известно, что при прессовании порошковых тел возникающие на контактных поверхностях материала на контактных поверхностях материалов со стенками пресс- форм силы внешнего трения вызывают неравномерное распределение давлений и плотностей в объёме уплотняемого тела.

Особенно наглядно это проявляется при прессовании относительно высоких брикетов, для которых теоретическое исследование закономерностей  распределения давлений, деформаций и плотностей представляет наибольший интерес.

Решение указанной задачи по определению распределения напряжений и плотностей выполнено в [1,2,3]

В настоящей работе рассматриваются вопросы дальнейшего развития теоретического исследования по определения полей напряжений, деформаций и плотностей, а также объёмного и линейного модулей упругости при прессовании металлических порошков в глухой цилиндрической матрице, когда удаётся удовлетворить краевым условиям по всему контуру прессовки как для напряжений, так и для перемещений, и получить достаточное простые для практических расчётов зависимости.

Используя основные положения теории сплошности, для осесеметричного одностороннего сжатия порошкового материала при небольших скоростях компактирования и отсутствие смещений материала в поперечной плосксти формовки (уплотнение в жёсткой матрице), когда массовыми силами  из-за  их малости по сравнению с поверхностными силами  можно пренебречь, уравнения равновесия в цилиндрических координатах запишутся:

                                                                                                                                   (1)

                                                                                                                                         (2)

Кроме того

                                                    (3)

Где ,, -осевое, радиальное, окружное нормальные напряжения;

        - касательные напряжения;

         - коэффициент бокового давления.

В дальнейшем, коэффициент бокового давления    считаем постоянной величиной в любой точку формовки, для чего используем среднее значение коэффициента для данного момента компактирования, как это сделано в (1,2)

Из совместного решения (1)-(3) будем иметь :

                                                                                                                   (4)

Где -среднее нормальное напряжение (изотропная составляющая тензора напряжений) .

Решение уравнения (4)  будем искать в виде :

                                                                                                                    (5)

Где - соответственно функция только от r b z .

Подставляя искомое выражение для  в (4) и производя разделение переменных, получим:

Где  -функция Бесселя  нулевого порядка мнимого аргумента;

      - функция Макдональда; .

В силу симметрии задачи r=0 следует, что =0.

Тогда:

,                                                                                                          (6)

Где А, , , k- произвольные постоянные, определяемые из краевых условий.

Экспериментальные кривые сжатия мелкодисперсной пыли при активном нагружении имеют сходство с диаграммами сжатия объёмно-твердеющих [4].

Для этих материалов зависимость между напряжением  и относительной линейной деформацией  достаточно точно может быть описана следующим выражением:

Где m,n- постоянные коэффициенты для данного материала и условий нагружения , при этом .

На конечном участке уплотнения, когда развиваются значительные усилия компактирования  и материал приобретает некоторую плотную структуру , перемещения среды будем рассматривать в рамках теории малых деформаций и связь между деформациями  и компонентами смещения можно принять в форме Коши, то есть:

 ,                                                                                                                              (7)

 где -смещение материала вдоль направления компактировния.

Из (6) и (7) имеем:

                                                                                                             (8)

Где .

Из практики и теории уплотнения известно, что существует сечение в формовке (), в любой точке которого давление компактирования постоянное и равняется своему среднему значению  .

При  (), , , где

Выражение (6) перепишем так :

Для сечения  и , когда  соответствует сечению под пуансоном , z=0 сечению на поддоне, Н- конечная  высота уплотняемой формовки, а .

Из (8)

                                                                                         (9)

Где  некоторая функция .

Разложим подинтегральное выражение в следующий сходящийся ряд:

И ограничимся первыми двумя членами, то есть :

                                                                                                      (10)

Из сравнения значений изменения функция и  при различных   следует, что при  для (что соответствует интервалу изменения и  в реальных процессах компактирования ) максимальные расхождения не превышают не превышают (10-12%).

Из (9) с учётом (10) и краевых условий на поддоне () найдём  и

                                                                                                       ,(11)

Где .

Из условия, что под пуансоном (z=H) и в любой точке , следует что

Подставляя найденное значение  в выражение ,для нормального напряжения  получим:

                                                                                                                     (12)

Условие равновесия всех сил приложенных в формовке конечной длины запишется:

                                                                                                            (13)

Где - коэффициент внешнего трения материала о боковую поверхность пресс-формы.

В первом приближении для мелкодисперсной пыли произведение  можно считать величиной постоянной, не зависящей от давления компактирования .

Их (12) и (13) мы найдём :

Где  - удельное давление уплотнения;

Р- усилие компактирования ;

- функция Бесселя первого мнимого аргумента;

- внутренний радиус пресс-формы.

Из условия

                                                                                                                      (14)

Найдём

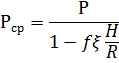
Подставляя найденные значения  и  в (12),  окончательно для  получим :

                                                                                                                  (15)

Где

Из (15) нетрудно увидеть, что в любой точке сечения  величина  остаётся неизменной.

Значение касательного напряжения (2) как

                                                                                                                         (16)

Где - некоторая функция от .

В предположении, что на торце пуансона касательные напряжения отсутствуют, то есть при z=H  τ=0, из (16) с учётом (15) найдём , и окончательное выражение для касательных напряжений запишутся следующим образом

                                                                                                                        (17)

Где

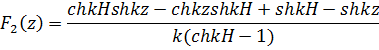
Относительная деформация  c учетом (11) определяется как

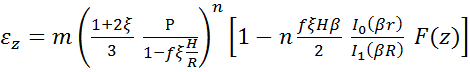                                                                                      (18)

А обьёмный  и линейный  модули упругости соответственно

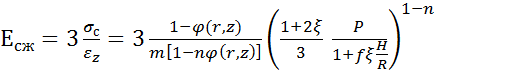                                                                                                                              (19)                                                                                                                          ,

Где  коэффициент Пуансон.

                                                                                                                             (20)

Значение параметра  k найдем из следующего условия, удовлетворяя в среднем по боковой поверхности формовки известное из закона сухого трения соотношения между касательными и нормальными напряжением

                                                                                                                         (21)

Подставляя в (20) выражения (15) и (17) , получим следующее выражение для определения k

                                                                                                                         (22)

Таким образом, выражения (15), (17), (3) и (22) полностью определяют поле для всех компонентов тензора напряжений в компактируемом материале, (18),(19), (20) распределение деформаций, обьёмного и линейного модулей упругости.

Для расчетов указанных величин необходимо знать геометрические параметры прессуемого брикета (радиус R, высоту H), удельное давление прессования p, значение коэффициентов бокового ξ, внешнего трения f, m и n.

Полученные теоретические зависимости сопоставлялись с результатами экспериментальных исследований других авторов.

На рис. 1 и 2 в виде сплошных линий представлены расчетные давления по боковой поверхности брикета из порошка восстановленного железа при удельном давления прессования р=4,0 Т/см².

Прессование одностороннее. Внутренний радиус матрице 25 мм. Соотношение размеров получаемого брикета  (рис.1) и  (рис.2). Значения ξ=0,50 и f=0,25 при р=4,0 Т/см² для порошка восстановленного железа были заимствованы из работы [5].

Значения коэффициентов m и n для различных металлических порошков определялись по истинным кривым сжатия и представлены в таблице.

Величина давлений под пуансоном и на поддоне рассчитывались по (15) соответственно для пуансона при Z=H и для поддона Z=0. Давление на боковую поверхность пресс-формы рассчитывалось из (3) и (15) при  r=R. Отдельными точками на рисунках 1 и 2 показаны экспериментальными значениями давлений на рабочей части пресс-формы, полученные в работе [6] с помощью штифтових датчиков. Как видно, имеется удовлетворительное согласование между теоритическими и экспериментальными результатами.

Используя известные выражения, связывающие давления и плотность при прессовании порошкових материалов, например [2,7] , и имея зависимость (15) для нормального напряжения ,и можно определить распределение плотности по объёму прес совки.

ЛИТЕРАТУРА

1.Жданович Г.М. Порошковая металлургия, № 6,1969.

2. Жданович Г.М. Теория прессования металлических порошков , «Металлургия», М.,1969

3.Рассказов Н.И. Труды МИХМ, ХХIX научно-техн. конф. М., 1968.

4. Колчин А.Д., Перлин П.И., Соколовский В.В. Порошковая металлургия, №1, 1970.

5.Меерсон Г.А., Ковынев Р.А., Полухин О.Ф. Порошковая металлургия,№1, 1970.

6.Федорченко И.М., Ковынев Р.А.,Полухин О.Ф. Порошковая металлургия, № 7, 1970.

7. Кунин Н.Ф., Юрченко Б.Д. Порошковая металлургия, №6, 1963.