К оптимизации кинематических параметров рычажных четырёхзвенных механизмов
Источник: Журнал «Экспозиция МашМетСварка»
http://www.mmsv.ru/articles/639/6023/
Современные информационные технологии достаточно адекватно решают многие сложные технические задачи автоматизированного проектирования (АП) технологических и механических систем, обеспечивая поэтапный процесс их параметрической оптимизации [1], достигая экстремальных значений принимаемых критериев качества.
Автор, как участник и свидетель более 45-летней эволюции электронных вычислительных машин (ЭВМ) в Советском Союзе и России, «переживший» многие и довольно частые смены поколений отечественных ЭВМ (от «Урал-1» до ЕС-1060 и персональных IBM), обладающий многолетним практическим опытом в построении систем АП, имеет основание выдвинуть предположение о том, что в первой половине XXI-го века будет создан искусственный интеллект для выбора, проектирования и оптимизации именно структур (т.е. кинематических схем, а не их параметров) любых механизмов и машин в широком диапазоне их предназначений. При этом, без сомнения, за конструктором сохранится выбор и принятие окончательного проектного решения. Если сейчас компьютер – это помощник и советчик конструктора, а также – рабочий инструмент в производстве чертежей деталей, узлов и машин в режиме АП, то в ближайшем будущем – это активный (совместно с визуальным и звуковым распознаванием и беспроводной связью) и равнозначный участник процесса оптимального проектирования сложных систем машин.
Кроме того, многообразные постановки задач оптимизации проектирования крайне актуальны и необходимы в условиях рыночной экономики, ибо надёжно обеспечивают повышение индекса перспективной конкурентоспособности страны и экономической эффективности новых создаваемых технологических производств. Известно [2], что широчайшая гамма конструкций механизмов в различных отраслях современной промышленности и бытовой техники основана на применении рычажных четырёхзвенников (механизма П.Л.Чебышёва), реализующих разнообразные технологические и кинематические задачи в машинах и агрегатах. Например, механизм ножного привода швейной машины, полиграфические и кондитерские производства, станкостроение и тяжёлое машиностроение и т.п. Подтверждением вышеупомянутого также является тот факт, что в Интернете рычажным, в том числе и четырёхзвенным механизмам посвящено более 43000 страниц на русском языке.
Шарнирные четырёхзвенные механизмы обладают уникальными свойствами и подбором длин рычагов и их исходного положения обеспечивают:
Достаточно много рычажных механизмов и в металлургических производствах, например, в прокатных цехах: толкатели (сталкиватели), кантователи, подъёмно-качающие столы, маятниковые пилы, рычажно-кривошипные летучие ножницы и другие. Поэтому их рациональное проектирование с достижением оптимальных значений критериальных функций является весьма прагматичной и часто решаемой конструкторской задачей.
На «Уралмашзаводе» ещё в середине 60-х годов прошедшего столетия, применительно к проектированию прокатного оборудования, были сделаны первые скромные шаги в решении задач оптимизации механических систем на ЭВМ, убедительная эффективность которых, в дальнейшем, привела к созданию ряда автономных систем АП технологий процессов прокатки, а также металлургического, горного, бурового и другого оборудования тяжёлого машиностроения.
Ниже представлена математически корректная постановка и результаты компьютерного решения одной из первых задач выбора оптимальных конструктивных параметров четырёхзвенного рычажного механизма сталкивателя слитков (заготовок) при воспроизведении заданной траектории движения его исполнительного звена (шатуна).
В большинстве случаев синтез механизмов с низшими парами позволяет только приближённо реализовать заданную траекторию.
Аналитическое решение такой задачи представляет собой известную математическую задачу о приближении функций, когда заданная функция приближённо заменяется другой, мало от неё отличающейся [3].
Обозначим заданную функцию, которую должен воспроизвести механизм, через y=F(x) , где x и y – координаты точек кривой, которая должна приближённо совпадать с траекторией какой-либо точки исполнительного звена. Воспроизводимую механизмом функцию обозначим через y=FM(x), вид которой зависит от геометрических параметров кинематической схемы – искомых величин. Последние должны быть выбраны таким образом, чтобы функция y=FM(x) на заданном отрезке изменения аргумента x возможно мало (с заданной погрешностью) отличалась от функции y=F(x).
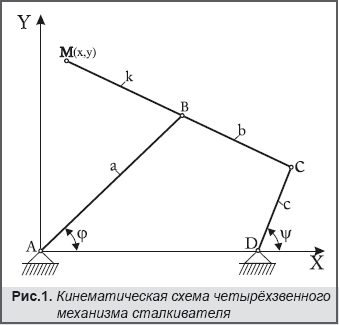
Принципиальная кинематическая схема механизма сталкивателя, представляющего собой классический шарнирный четырёхзвенник, показана на Рис.1. В качестве тестовой задачи представим её решение, приближая траекторию т. М шатунной кривой (шатун – звено МС) к прямой линии y=1,145 на заданном интервале изменения x [x1, x2].
Все аналитические выкладки произведены в относительных единицах, при длине стойки четырёхзвенника принятой равной единице, т.е. АД=1. Обозначения длин звеньев механизма показаны на Рис.1, где ψ и φ – углы поворота соответственно ведущего звена СД и ведомого – АВ, МС=b, MB=k. Итак, искомыми параметрами являются величины a, b, c и k.
Составим уравнение шатунной кривой. Выражая координаты точки В через линейные и угловые параметры четырёхзвенника, после ряда последовательных математических преобразований, уравнение шатунной кривой (для точки М) может быть представлено в следующем виде:
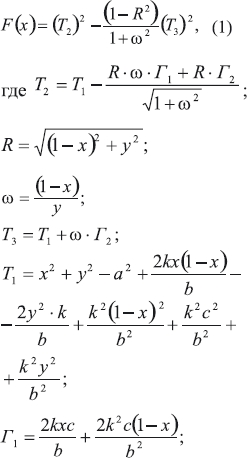
Начальные координаты точки М - x0 и y0. Приближаем шатунную кривую к прямой линии y=1,145 на отрезке [x0, x0 +0,28].
Известно, что простейшим видом приближения функций является интерполирование, т.е. совпадение значений функций y=F(x) и y=FM(x) в n точках рассматриваемого интервала изменения аргумента x, где n – число неизвестных параметров (или узлов интерполяции).
Аналитическое решение задачи о нахождении неизвестных параметров приближающей функции y=FM(x) в данном случае сводится к решению n уравнений, которые образуются, если приравнять нулю величины разности Δ=F(x) – FM(x) в n точках, т.е.
Δ(xi)=F(xi) – FM(xi)=0.
Обычно отрезок приближения разбивают на узлы интерполяции по формуле П.Л.Чебышёва [3], в нашем случае получаем четыре точки –
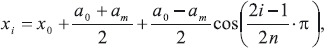
где i=1,2,3,4; a0=0; am=0,28. Принимаем, что шатунная кривая пересекается с прямой y=1,145 в этих точках, а из данных условий и определяем параметры a, b, c и k.
Итак, имеем
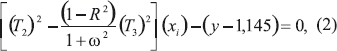
где i=1,...,4 и y=1,145.
Для решения полученной системы нелинейных уравнений (2) применён метод скорейшего спуска [4]. Составляем функцию:
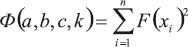
и находим аналитические выражения для частных производных:
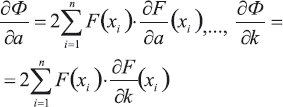
и для
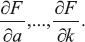
Решение системы нелинейных уравнений получаем из следующей формулы:
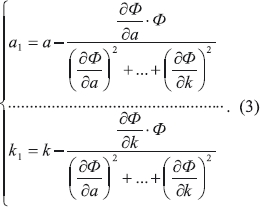
Подставляя в систему (3) выражения для частных производных находим a1, b1, c1 и k1; если |a1-a|<10-6,…, |k1-k|<10-6, то прекращаем счёт, иначе принимаем: a=a1, b=b1, c=c1, k=k1 и снова продолжаем счёт по формуле (3).
Величины максимального отклонения кривой, описываемой т.М шатуна, от прямой y=1,145 также рассчитываются по аналитическим зависимостям, как функциям параметров четырёхзвенника, на основе численного итеративного метода.
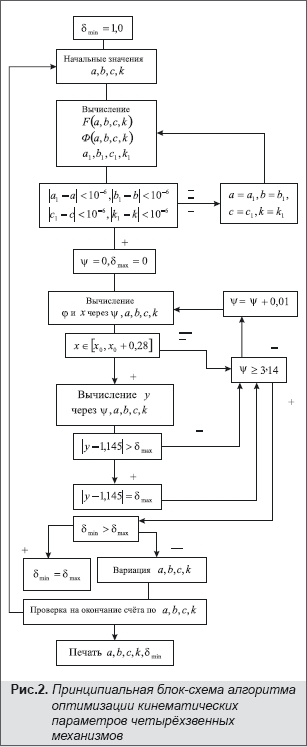
Решение системы нелинейных уравнений, естественно, зависит от начальных значений a, b, c и k, поэтому варьируя величинами последних в их допустимых областях, получаем каждый раз свои величины максимальных отклонений – δmax от заданной прямой и выбирая минимальное δmin из них, соответствующие δmin кинематические параметры и будут искомыми величинами. Принципиальная блок-схема алгоритма расчёта показана на Рис.2.
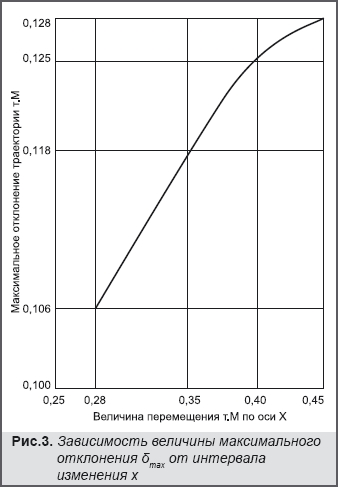
Величина отклонения существенно зависит от длины отрезка, на котором изменяется аргумент x: чем длиннее отрезок, тем больше отклонение, что естественно. Но прослеживается тенденция к насыщению прироста величины отклонения с увеличением перемещения исполнительного звена механизма, что убедительно иллюстрирует Рис.3.
Расчёты по представленному алгоритму были проведены на ЭВМ (если мне не изменяет память – это «Урал-4» или «Минск-2») и получены следующие результаты: оптимальные величины (в относительных единицах) кинематических параметров механизма – a=0,816, b=2,226, c=0,299 при x1=-1,0 и x2=-0,72 и минимальном отклонении от воспроизводимой прямой y=1,145, равном 0,097.
Разработанный алгоритм пригоден и для оптимизации шарнирных четырёхзвенников при воспроизводстве траекторий в виде плоских кривых линий. В частности, для дуги окружности радиусом 1,145 получены такие результаты: a=0,645, b=2,141, c=0,312.
Таким образом, представленная математическая постановка и созданный алгоритм для оптимизации кинематических параметров плоских рычажных четырёхзвенных механизмов, рекомендуется к применению в системах автоматизированного проектирования.
Искомые линейные и угловые параметры механизма и преемлемая точность исполнения траектории являются оптимальными только для одного, расчётного, перемещения
Но механизм, чаще всего, выполняет различные технологические перемещения из весьма широкого диапазона, для которых выбранные параметры уже не будут оптимальными.
Поэтому, если необходимо точное исполнение заданной траектории для всего диапазона перемещений, рекомендуется применить микропроцессорное программное управление для коррекции исходных положений рычагов и режимов работы электропривода механизма.
В заключение хотелось бы отметить следующее. Интуиция автора всё же подсказывает, что в ближайшем будущем новые поколения компьютеров позволят уверенно заменить громоздкие многомощные механические (в том числе и рычажные) системы на быстродействующие программируемые электронные устройства (совместно с роботами и сенсорами), выполняющие всю широту прежних функций. По крайней мере, автор уверен в том, что конструкции многих рычажных механизмов будут постепенно упрощаться за счёт применения микропроцессорных устройств.