Обязательной процедурой при решении указанной задачи является поиск оптимальных режимов обработки. Применительно к процессам шлифования наиболее распространенным и одним из наиболее точных методов до настоящего времени является классический экспериментально-теоретический метод нахождения режимов, который включает следующие этапы [1]:

• составление системы уравнений, описывающих технические ограничения, налагаемые на режимы резания требованиями к детали, станком, инструментом и условиями производства;
  
• математическое описание целевой функции, которая выражает цель оптимизации;
  
• совместное рассмотрение технических ограничений и целевой функции и определение на этой основе оптимального режима шлифования.

Главным недостатком указанного метода, существенно ограничивающим практические возможности его использования в технологической подготовке производства деталей из новых конструкционных материалов или в условиях шлифования кругами с новыми характеристиками, является его высокая трудоемкость, обусловленная большими затратами времени на эксперименты, необходимые для получения всех уравнений и зависимостей, описывающих технические ограничения.

Авторами на протяжении длительного времени ведутся исследования, связанные с изучением следующих вопросов:

– определение параметров процесса шлифования, обеспечивающих заданную шероховатость обработанной поверхности [2];

– нахождение допустимой силы взаимодействия рабочей поверхности круга (РПК) с поверхностью заготовки, при которой не произойдёт фазово-структурных изменений в поверхностном слое обрабатываемой заготовки [3];

– нахождение допустимой силы взаимодействия РПК с поверхностью заготовки, при которой не произойдёт изменений физико-химических свойств инструментального материала [4, 5];

– поиском интегрального технического ограничения на режимы шлифования, обеспечивающие максимальную производительность при соблюдении заданных требований по качеству обработки [4,5].

По результатам проведенных исследований разработан ряд методик, позволяющих определять элементы режима обработки для различных материалов и условий шлифования при условии соблюдения всех требований к качеству обработанной поверхности. В связи с этим целью данной работы является составление целостного комплекса методик назначения режимов шлифования, обеспечивающих стабильные пока-затели качества обработки, и определение обобщенных режимных параметров процесса для упругой и жесткой схем обработки.

Основное содержание работы

Рассмотрим комплекс методик, применяемых для определения оптимальных режимов плоского врезного алмазного шлифования с электроэрозионными воздействиями на РПК (по упругой схеме) в соответствии с предложенной нами последовательностью оптимизации, которая включает следующие этапы [6]:

1) расчет скорости детали, при которой достигается требуемая шероховатость обработанной поверхности;

2) расчет максимально допустимого усилия поджима заготовки к кругу в процессе шлифования по упругой схеме, при котором удовлетворяется лимитирующее техническое ограничение;

3) экспериментальное определение закона изменения предельной режущей способности круга во времени при шлифовании по упругой схеме, кинематически аналогичной жесткой;

4) определение режимов электроэрозионных воздействий на РПК, обеспечивающих минимальную удельную себестоимость обработки, с учётом явлений, вызвавших ухудшение режущих свойств круга;

5) описание закона изменения глубины шлифования по упругой схеме в соответствии с законом изменения предельной режущей способности круга без учёта процесса засаливания РПК;

6) определение величины подачи на врезание по жёсткой схеме.

Скорость детали V_д рассчитывается исходя из необходимости обеспечения заданной высоты неровностей профиля шлифованной поверхности R_a [7]. Для этого определяется отношение скоростей 60V_к /V_д, при котором поперечное перекрытие срезов должно произойти на интервале

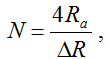
где R – принятая величина интервала, мкм.

При плоском врезном шлифовании отношение скоростей круга и детали будет иметь вид [7]:

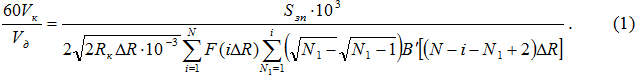
где S_зп – расстояние между зернами на рабочей поверхности круга, мм;

N – номер исследуемого интервала;

i – номера интервалов, входящих в N; i = 1, 2, ... N;

N₁ – участки поверхности круга, обрабатывающие i-е интервалы; N₁ изменяется внутри i от 1 до N – i + 1;

F(iR) – вероятность попадания вершин алмазных зёрен в i-й интервал;

B(iR) – ширина среза на i-м интервале, мкм.

В процессе обработки параметр R_a , обеспечиваемый соотношением (1), будет только уменьшаться вследствие образования и увеличения размеров контактных площадок на зёрнах, засаливания рельефа и микрорельефа РПК и т.п. Соответственно, отношение скорости круга к скорости детали является обобщенным режимным параметром, обеспечивающим требуемую шероховатость обработанной поверхности в любой момент времени обработки.

При шлифовании по упругой схеме с поддержанием постоянной радиальной силы поджима заготовки к шлифовальному кругу P_п = P_y предельное значение этой силы определяется исходя из лимитирующего технического ограничения, чаще всего связанного с теплонапряженностью процесса обработки.

Для труднообрабатывемых высоколегированных сталей максимально допустимое усилие поджима заготовки к кругу P_п определяется исходя из критической температуры T_кр, выше которой происходят фазово-структурные изменения в обрабатываемом материале. Связь максимальной температуры поверхности резания с параметрами процесса шлифования представлена формулой, в которой тангенциальная составляющая силы резания учтена через коэффициент шлифования K_ш = P_z /P_y :

где M – коэффициент, определяемый по формуле M = 1 + 2(/4 – );

a_z – максимальная толщина среза, мм;

b – ширина единичного среза, мм;

 – соответственно угол сдвига и угол действия;

K_з – коэффициент, учитывающий закон распределения нормальных напряжений на поверхности контакта зерна с деталью;

f_з – площадь зоны контакта задней поверхности зерна с деталью, мм²; в принятой нами модели зерна f_з = b·l_z , (здесь l_z – длина контактной площадки на задней поверхности зерна);

z_р – количество одновременно контактирующих с деталью зёрен;

a,  – соответственно коэффициент температуропроводности, м²/с, и теплопроводности, Вт/(м·K), обрабатываемого материала;

H – безразмерная полуширина источника тепла;

S – площадь зоны контакта детали со шлифовальным кругом, мм²;

C,  – начальная ордината и коэффициент в линейной зависимости, отражающей влияние температурно-скоростных факторов на величину касательных напряжений; зависимость имеет вид _s = C – T.

Величины, входящие в формулу (2), рассчитываются по зависимостям и методикам, приведенным в работе [2].

Условие, выполнение которого обеспечивает отсутствие фазово-структурных превращений в материале заготовки при обработке, представим в виде неравенства

0,98T_кр < T < 1,00T_кр,

и решим его относительно t_ф, с учётом (2), пошаговым методом с использованием параметров РПК, сформированных во время правки. Найденное значение является максимально возможной исходной глубиной шлифования t₀, обеспечивающей отсутствие фазово-структурных изменений в поверхностном слое (дефектов на поверхности заготовки) в начале обработки.

Используя t₀, по составленной программе для ПЭВМ рассчитывается допустимое значение радиальной составляющей [P_y], которое должно поддерживаться постоянным посредством упругого поджима заготовки к РПК на протяжении всего времени обработки, по следующей формуле

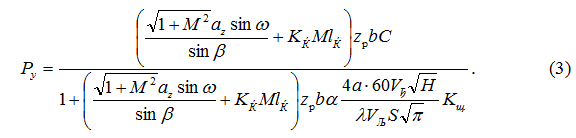
Рассчитанное по уравнению (3) значение составляющей [P_y] принимается в качестве максимально допустимой силы поджима заготовки к кругу P_п, которая является обобщенным режимным параметром процесса, обеспечивающим стабильность структуры и физико-механических свойств поверхностного слоя обрабатываемого материала и материала инструмента.

Для расчета допустимого значения радиальной составляющей [P_y] необходима информация о параметрах единичного среза. Размеры единичного среза характеризуются длиной, фактической толщиной и шириной среза.

Длина сегментообразного среза рассчитывается по формуле

запятообразного – по формуле

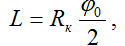
где R_к – радиус шлифовального круга;

φ₀ – угол контакта зерна с заготовкой.

Максимальная толщина сегментообразных срезов соответствует фактической глубине резания.

Как установлено нами, в результате отсутствия сплошной режущей кромки на РПК влияние подачи на врезание t на фактическую глубину резания t_ф зависит от соотношения величины подачи и максимальной высоты неровностей шлифованной поверхности R_max:

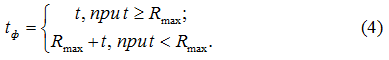
Поскольку удаление материала с поверхности резания запятообразными срезами осуществляется таким же образом (как указано выше), в условиях отсутствия сплошной режущей кромки, то, по аналогии с глубиной резания (формула (4)), максимальную толщину среза необходимо оценивать максимальной фактической его толщиной, учитывая соотношение величины a_z и максимальной высоты неровностей профиля поверхности резания R_{max пр}.

Для расчета высоты неровностей поверхности резания была разработана методика [7], которая позволяет установить наличие превышения величиной R_{max пр} значения максимальной толщины среза a_z. Тогда, соответственно, максимальная фактическая толщина среза определяется следующим образом:

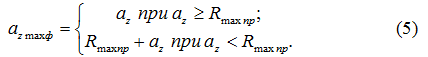
Значения максимальной фактической толщины среза, определенные с использованием выражения (5), используются для расчетов по формулам (1) и (3).

При шлифовании по упругой схеме с поддержанием постоянной радиальной силы поджима заготовки к шлифовальному кругу P_п = P_y потеря со временем режущей способности РПК проявляется через изменение глубины шлифования. Таким образом, эволюция подсистемы резания во времени в результате ухудшения режущих свойств РПК однозначно описывается изменением во времени фактической глубины шлифования t_ф = f().

Закономерность изменения глубины шлифования t_ф во времени обработки  по упругой схеме вследствие ухудшения режущих свойств РПК в результате процессов изнашивания зёрен, засаливания межзёренного пространства, засаливания микрорельефа зёрен и т.п, описываем экспоненциальным выражением вида

t_ф() = t_уст + t·exp(),                        (6)

где t_уст – установившаяся глубина шлифования;

t = t₀ – t_уст – амплитуда снижения глубины шлифования;

t₀ – исходная глубина шлифования рельефом РПК, параметры которого сформированы после электроэрозионной правки;

Уравнение (6) отражает закон изменения предельной режущей способности шлифовального круга во времени при обработке по упругой схеме и является передаточной функцией, позволяющей обеспечить одинаковые условия работы зёрен при упругой и кинематически аналогичной жесткой схемах обработки.

Полученные данные и зависимости используются для назначения режимов обработки для более распространённой в промышленности жёсткой схемы шлифования.

При осуществлении обработки по жёсткой схеме на станках с ЧПУ подача на врезание назначается для каждого i-го хода (или прохода при шлифовании с подачей) круга таким образом, чтобы её значение не превысило глубину шлифования, рассчитанную по уравнению (6), для времени обработки

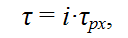
где i – номер хода (прохода) шлифовального круга;

τ_рх – время рабочего хода шлифовального круга, мин.

При шлифовании по жёсткой схеме на универсальных станках без программного управления подача на врезание назначается из условия отсутствия фазово-структурных превращений в поверхностном слое детали по минимальному значению глубины резания, определённому из уравнения (6) для заданной продолжительности технологического перехода.

При шлифовании с электроэрозионными управляющими воздействиями на РПК главной задачей таких воздействий является достижение такого характера протекания процесса обработки (когда изменение режущих свойств шлифовального круга описывается зависимостью (6)), при котором установившаяся глубина шлифования t_уст насколько можно более приблизилась бы к максимально возможной исходной глубине шлифования t_о, при которой обеспечивается отсутствие фазово-структурных изменений в поверхностном слое (дефектов на поверхности заготовки) в начале процесса обработки. Такое сближение приводит к более рациональному использованию режущих свойств шлифовального круга и снижению удельной себестоимости обработки на шлифовальных станках.

Выводы

1. К обобщенным режимам шлифования относятся те параметры процесса обработки, задание значений которых перед началом обработки обеспечивает стабильные показатели качества шлифованной поверхности. Такими обобщенными режимными параметрами процесса шлифования для упругой и жесткой схем обработки, которые могут быть найдены по рассмотренному комплексу методик, являются соотношение скоростей круга и детали, а также сила поджима заготовки к кругу P_п.

2. Наиболее эффективное использование режущих свойств шлифовального круга при упругой схеме обработки осуществляется автоматически, за счет изменения фактической глубины шлифования.

3. Для жёсткой схемы обработки передаточной функцией, позволяющей обеспечить одинаковые условия работы зёрен, является закон изменения режущей способности РПК, полученный экспериментально на кинематически аналогичной упругой схеме. По этому закону необходимо назначать подачу на врезание для жёсткой схемы.

Список литературы

1. Абразивная и алмазная обработка материалов. Справочник/ Под ред. А.Н. Резникова. – М.: Машиностроение, 1977. – 391 с.

2. Матюха П.Г. Научные основы стабилизации выходных показателей алмазного шлифования с помощью управляющих воздействий на рабочую поверхность круга: Автореф. дис.... докт. техн. наук: 05.03.01 / Матюха Пётр Григорьевич, Харьк. госуд. политехн. ун-т. – Харьков, 1996. – 48 с.

3. Полтавец В.В. Обоснование режимов шлифования труднообрабатываемых материалов при электроэрозионном воздействии на рабочую поверхность круга: Автореф. дис…. канд. техн. наук: 05.03.01 / Полтавец Валерий Васильевич, Донецк. национальн. техн. ун-т. – Донецк, 2001. – 19 с.

4. Матюха П.Г. Определение режимов плоского шлифования твердых сплавов с использованием нового критерия о текущей лимитированной режущей способности круга/ П.Г. Матюха, В.Б. Стрелков, В.В. Полтавец // Сверхтвердые материалы. Научно-теоретич. журнал. – Киев: 2004. – № 3. – С. 67-73.

5. Матюха П.Г. Определение оптимальных режимов при алмазном шлифовании твердых сплавов по упругой схеме с периодическими электроэрозионными воздействиями на рабочую поверхность круга / П.Г. Матюха, В.Б. Стрелков // Сучасні технології в машинобудуванні. Зб. Наукових статей/ Уклад. А.І. Грабченко: За заг. ред. А.І. Грабченка. – Харків: НТУ „ХПІ”, 2007. – С. 332-332.

6. Матюха П.Г. Определение оптимальных режимов шлифования с электроэрозионными управляющими воздействиями на рабочую поверхность круга/ Физические и компьютерные технологии в народном хозяйстве. / П.Г. Матюха, В.В. Полтавец // Труды 8-й международной научн.-техн. конф. 9-10 декабря 2003 г. – Харьков: ХНПК “ФЭД”, 2003. – С. 151-155.

7. Матюха П.Г. Исследование высоты неровностей профиля поверхности резания при шлифовании / П.Г. Матюха, Л.К. Терехова // Резание и инструмент. Респ. межвед. научно-техн. сб. – Харьков: Изд-во “Основа”. – 1990. – Вып. 44. – С. 114-121.

---

Библиотека