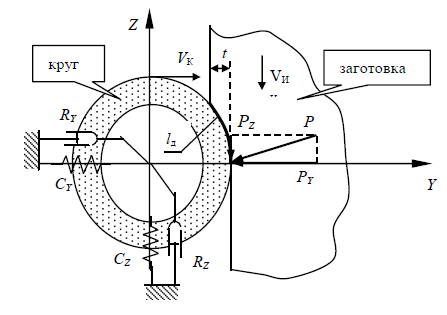
Рисунок 1 - Схема контакта шлифовального круга
| Библиотека |
Процесс шлифования занимает большое место в современном машиностроении как один из финишных методов обработки. Причем высокие скорости резания при шлифовании и формообразование в тонких приповерхностных слоях материала вызывают значительные механические и тепловые нагрузки, приводящие иногда к трещинам и прижегам на обработанных поверхностях. Это ухудшает качество обработки. С другой стороны, высокие температуры при шлифовании воздействуют на шлифовальный круг, приводят к выгоранию связки, затуплению зерен, повышенному износу, что снижает производительность и ухудшает условия обработки.
До настоящего времени тепловые и динамические процессы при шлифовальной обработке исследовались раздельно. Но при использовании предельных режимов резания и повышении требований к точности обработки постоянные времени этих процессов в зоне резания становятся сравнимыми. Поэтому динамическое поведение технологического оборудования можно предсказать только с учетом комплексного воздействия тепловых и упругих процессов.
В данной работе предлагаются математическая модель и методика расчетов тепломеханических процессов при абразивной обработке как часть комплексной теплодинамической системы шлифовального станка. Для построения математической модели использован метод электрической аналогии [2], который позволяет отразить как тепловые, так и процессы другой физической природы.
Шлифование как процесс пластического деформирования и разрушения материалов детали и круга занимает промежуточное положение между резанием резцом [3, 4] (инструментом с определенной режущей кромкой) и трением. Поэтому при моделировании динамики процесса при шлифовании необходимо учесть особенности этого процесса. Математические модели должны учитывать, что изменения условий обработки (подача, ширина круга, зернистость и т. д.) влияют на силы резания через изменение фактического, а не номинального сечения срезаемого слоя. Схему контакта шлифовального круга с заготовкой можно представить в соответствии с рис. 1.

Рисунок 1 - Схема контакта шлифовального круга
Процесс удаления материала с заготовки на длине контакта lд обеспечивают отдельные зерна. Пока еще нет достаточной информации о процессах стружкообразования, силах и трении при резании абразивными и алмазными зернами. Но, ссылаясь на публикации [1, 9, 10] и информацию о виде стружек при шлифовании, можно предположить близкое сходство процесса резания зерном и резцом (рис. 2). Процесс отделения стружки отдельным зерном содержит три фазы упругопластического взаимодействия: фаза чистой упругой деформации, фаза упругой и пластической деформации, фаза упругой и пластической деформации с удалением материала. При этом значения составляющих совокупной силы резания могут быть вычислены по следующим выражениям.
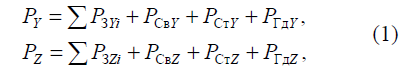
где PЗYi, PЗZi, PСвY, PСвZ, PСтY, PСтZ, PГдY, PГдZ – радиальная и тангенциальная составляющие силы резания соответственно при микрорезании единичным зерном, от контакта материала со связкой круга, от контакта материала со стружкой, заполняющей поры круга, от воздействия гидродинамических потоков в области контакта детали с кругом.
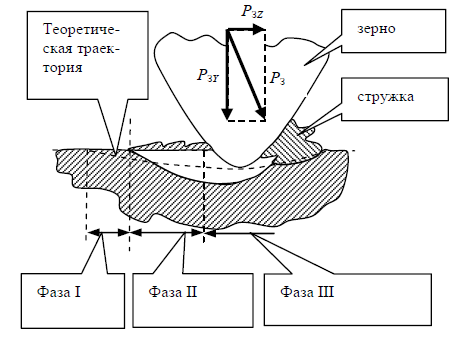
Рисунок 2 - Процесс резания отдельным зерном
Ограничим свое внимание первым слагаемым, которое наиболее тесно связано с кинематикой процесса и формированием обрабатываемой поверхности. Остальные составляющие мало зависят от относительного смещения круга и заготовки и их можно принять постоянными величинами и учесть в модели постоянными внешними усилиями.
Для определения PЗYi, PЗZi учтем систему сил, действующую на режущий выступ абразивного зерна (рис. 3) [4], и износ зерна при обработке.
При прохождении абразивным зерном зоны контакта детали с кругом силы резания изменяются синхронно с изменением глубины микрорезания a. Ширина площадки на вершине абразивного зерна связана с глубиной микрорезания зерна и с учетом формы зерна можно принять b = 2a.
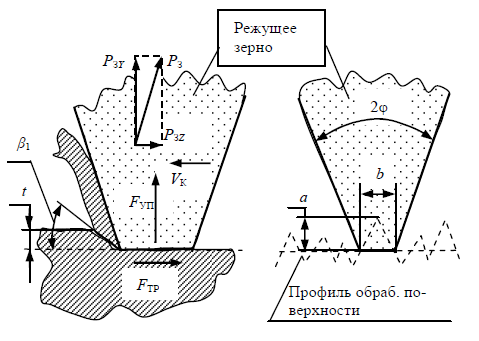
Рисунок 3 - Воздействие системы сил на режущий выступ зерна
При моделировании динамики процесса резания при шлифовании процесс резания будем отображать в виде полной линейной модели [3, 4, 5], так как процесс микрорезания зерна соответствует процессу резания резцом.
При этом процессы микрорезания зерен, находящихся в контакте с заготовкой, представим в виде некоторого совокупного процесса (2).
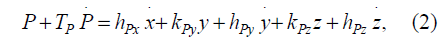
где kPx, kPy – коэффициенты резания по осям x, y, hPx, hPy , hPz – коэффициенты демпфирования по координатам x, y, z.
Коэффициенты резания по осям y и z при шлифовании можно вычислить по выражениям (3):
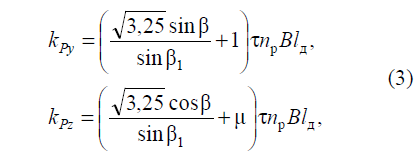
где β – угол между равнодействующей силой резания и скоростью резания,
β1 – угол сдвига,
τ – среднее касательное напряжение в плоскости сдвига,
np – фактическое число зерен, участвующих в резании, на единице площадки контакта круга с заготовкой,
B – ширина контакта круга с заготовкой,
lд – длина контакта круга с заготовкой,
μ – коэффициент трения стружки о поверхность зерна.
Величину фактического числа зерен, участвующих в резании, на единичной площадке контакта круга с заготовкой можно определить, исходя из законов теории вероятности, по выражению (4) [6, 7, 8]:
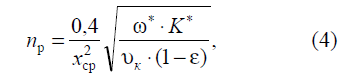
где Хср – средняя величина зерна, мм,
K* – концентрация режущего материала в круге, %, Vk – скорость шлифования, м/с,
ε – относительная глубина заделки зерен, (ε=0,7…0,8),
– скорость погружения зерен в обрабатываемый материал, мм/с.
В данной модели учитывается жесткость и демпфирование по ортогональным координатам z, y, которые определяют величину сечения срезаемого слоя материала.
По координате x учитывается только демпфирование резания. В левой части уравнения отражена инерционность процесса резания. Несмотря на то, что постоянные времени процесса резания при шлифовании невелики, намного меньше, чем при обработке лезвийным инструментом, мы пытаемся в модели учесть их влияния.
Абразивные и алмазные круги, применяемые при шлифовании, являются инструментами со стохастическим (вероятностным) расположением множества элементарных режущих зерен. В месте расположения каждого из зерен с материалом заготовки выделяется теплота, возникающая в процессе срезания отдельной стружки. Расположение этих локальных источников тепловыделения на поверхности контакта между заготовкой и кругом в связи со стохастическим размещением зерен непрерывно меняется во времени. Это приводит к выравниванию температур на всей контактной поверхности заготовки. Выравниванию температур содействует также явление самозатачивания. Эти особенности процесса шлифования позволяют при отображении тепловых процессов ориентироваться на схематизированное зерно с некоторыми усредненными геометрическими параметрами и условиями работы.
Для практического теплофизического анализа процесса шлифования будем использовать систему тел и источников в локальной области, прилежащей к зерну [6, 9, 10], согласно рис. 4.

Рисунок 4 - Режущий выступ зерна и расположение источников тепловыделения
Данная схема представляет режущий выступ зерна как элементарный резец с отрицательным передним углом. В схеме учитываются три источника тепловыделения: от деформации qд, от трения на поверхности контакта зерна с обрабатываемым материалом qтз и от трения передней поверхности зерна со стружкой qтп.
Теплота от каждого элементарного источника распределяется между всеми телами, участвующими в процессе. Представим это распределение в виде итоговых потоков теплообмена между инструментом, заготовкой и стружкой [6, 7, 8, 9, 10].
Итоговые потоки тепла определяем как результат совокупности элементарных потоков, соединенных параллельно. Элементарные источники представим аналогично в виде соответствующих совокупных источников.
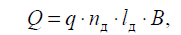
где nд – средневероятное количество режущих зерен, активно участвующих в процессе шлифования на единице контакта,
lд – длина контакта,
B – ширина контакта.
Математическая модель теплодинамической системы шлифовального станка при врезном шлифовании представляет собой систему обыкновенных дифференциальных уравнений с постоянными коэффициентами:

где θ1,2,3,4,5 – средние температуры характерных элементов исходной системы шлифовальной обработки: средняя температура стружки; средняя температура на передней поверхности зерна (температура резания), средняя температура в теле режущего зерна, средняя температура на задней поверхности зерна; средняя температура изделия;
kPн, kPя – коэффициенты резания по соответствующим координатам;
hPx, hPy, hPz – коэффициенты демпфирования резания по соответствующим координатам;
kx, ky, kz – коэффициенты, определяемые проекциями силы резания на соответствующие оси;
Qд – теплота деформации (в ваттах);
b* – коэффициент распределения теплоты деформации между изделием и стружкой;
Qтп – источник теплоты трения стружки по передней поверхности;
Qтз – источник теплоты трения заготовки по задней поверхности;
Rтп – определяет теплообмен между стружкой и передней поверхностью зерна;
Rтз – аналогично, определяет теплообмен между изделием и задней поверхностью зерна;
Rс – отражает отвод тепла со стружкой из зоны резания;
Rи – учитывает теплоотвод из зоны резания в глубину изделия за счет его относительного движения;
RZ, RY – отражают теплообмен между задней и передней поверхностями зерна;
Rк – учитывает отвод тепла от зерна в связку круга;
Ci – учитывают теплоемкость участков.
Использование для анализа полученной математической модели (5) позволило получить основные зависимости и характеристики взаимодействия упругой и тепловой систем при врезном шлифовании.
На рис. 6 показан переходный процесс изменения температуры резания θ2 при врезании шлифовального круга.
При врезании шлифовального круга в заготовку открывается переходный процесс, связанный с колебаниями упругой системы. Несмотря на то, что тепловые процессы не обладают инерционностью, это приводит также к колебательному переходному процессу в тепловой системе. Из переходного процесса видно, что установившееся значение температуры резания возникнет спустя некоторое время, определяемое тепловыми сопротивлениями.
На рис. 5 приведена амплитудно-частотная характеристика изменения температуры резания θ2 при периодическом изменении силы резания.
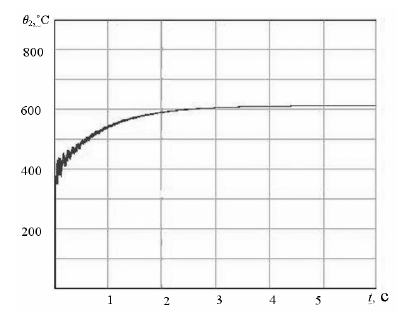
Рисунок 5 - График изменения температуры резания при врезании инструмента
На рис. 6 приведена амплитудно-частотная характеристика изменения температуры резания θ2 при периодическом изменении силы резания.
Периодическое изменение силы резания существенно снижает температуру резания в сравнении с установившимся значением. Эффект снижения достигается уже при небольших частотах. Это явление широко используется при шлифовании, когда реализуют процесс прерывистого шлифования. Однако следует иметь в виду, что при некоторых частотах в силу резонансных явлений в технологической системе возможно значительное увеличение температуры резания. Резонансные пики на графике определяются собственными частотами привода шлифовального круга, привода подачи заготовки, несущей системы станка и процесса резания. Если использовать сложные модели этих узлов станка, то их влияние будет еще более многообразным. Следует учитывать также резонансы температур от периодических возмущений в узлах технологического оборудования.

Рисунок 6 - Амплитудно-частотная характеристика изменения температуры резания при периодическом изменении силы резания
Полученная математическая модель (5) описывает основные теплодинамические процессы при врезном шлифовании. Она обладает достаточной гибкостью и универсальностью, позволяет отображать нюансы тепловых и механических упругих процессов при различных условиях обработки, в том числе исследовать проблему отвода тепла со смазочно-охлаждающей жидкостью. В то же время ее компактность позволяет встраивать ее в более сложные системы.
Предложенная методика и математическая модель могут быть использованы при исследовании особенностей теплодинамических процессов в шлифовальных станках при резании.