РАЗВИТИЕ ПРЕДСТАВЛЕНИЙ О ВИБРАЦИЯХ ПРИ РЕЗАНИИ
Автор: Е.А. ЧернышевУчебное заведение: каф. ТМ, ДонНТУ, г. Донецк, Украина
Известно, что процесс резания обычно сопровождается вибрациями. Зачастую они носят вредный характер, поэтому их стараются уменьшить технологическими или конструктивными методами. Между тем до сих пор нет единого и окончательного представления о причинах возникновения вибраций при резании металлов. Несмотря на кажущуюся простоту, ответить на этот вопрос пока не удалось. В данной работе ставится цель – проследить развитие представлений о причинах возникновения вибраций при резании. Для этого необходимо рассмотреть различные толкования происхождения вибраций и изменение подходов к исследованию динамических процессов при резании.
Предмет исследования, несмотря на всю его кажущуюся очевидность, является исключительно сложным. Так, общеизвестно, что наиболее распространенным способом описания силы резания есть ее вычисление с помощью эмпирических зависимостей. Ясно, что этот подход является инженерным по своей сути. Он позволяет прогнозировать среднюю величину усилия резания, но не рассматривает физической сущности процесса резания. Например, для вычисления силы резания при точении используется формула, в которой только три конкретных величины (режимы резания) и девять поправочных коэффициентов.
Можно привести второй пример, показывающий нерешенность поставленного вопроса. Все теоретические исследования вибраций в той или и той степени связаны с решением уравнений динамики. Но при самом поверхностном анализе выявляется, что уравнение динамики, связывая динамические переменные, не вносит никаких подвижек в решение вопроса: почему возникают вибрации? Например, если даже считать, что сила резания постоянна, то в простейшем случае для одномассовой системы с одной степенью свободы уравнение без затухания будет иметь вид . Очевидно, что уже в этом случае решением будет гармоническая функция, хотя сама сила резания постоянна. Это происходит потому, что, записывая само уравнение динамики с инерционным и упругим членами, тем самым постулируется существование вибраций. Их предполагает сама форма дифференциального уравнения. Ведь известно, что элементарные трансцендентные функции
и
по определению представляются как решения дифференциального уравнения
. Таким образом, составление и решение уравнение динамики не приближает к решению поставленного вопроса: почему при резании возникают вибрации? Этот пример показывает, что задача носит принципиально не математический характер (хотя применение математических методов в исследовании колебаний неизбежно).
Одним из первых объяснений возникновений колебаний при резании было естественное предположение о том, что усилие резания благодаря периодическому образованию и сколу элементов стружки является переменным, вызывая ритмические колебания. Это предположение, встречается, в частности, у Н.И. Резникова [1]. В работе В.С. Штейнберга [2] эта гипотеза получила развитие на основе экспериментальных исследований вибраций при резании, в которой автор приходит к выводу, что колебания носят вынужденный характер и происходят при совпадении частот вынуждающей силы (резания) и собственных колебаний. Убедительность экспериментальных доказательств, подтвержденных расчетами, на первый взгляд не оставляет сомнений в правильности исходной посылки.
Тем не менее следует признать этот случай характерным в истории науки, когда экспериментальное обоснование в конечном итоге не служит критерием истины. Б. Рассел приводит на этот счет забавный пример. Предположим, что хлеб делается из камня и камень съедобен. Рассуждая логически, приходим к выводу, что хлеб съедобен. Полученный вывод подтверждается экспериментально. Однако исходные допущения при этом остались ложными. Подобное явление отмечали многие выдающиеся ученые: экспериментатор ставит опыт, уже имея в голове некоторые ожидания, и поэтому зачастую видит то, что надеется увидеть. К сожалению, это характерно и для теоретиков.
Возвращаясь к основной теме, заметим, что вынужденный характер вибраций был отвергнут примерно в то же время. В 1933 г. Н.Л. Кайдановский и С.Э. Хайкин предположили, что колебания при резании не являются вынужденными. Это направление было поддержано в 1930-х гг. Н.С. Ачерканом, Г. Шлезингером, Н.А. Дроздовым [3] и получило дальнейшее развитие в 1940-х гг. в фундаментальных работах А.И. Каширина [4] и А.П. Соколовского [5]. В частности, в прекрасной книге [4] довольно подробно изложен анализ и критика объяснения вибраций как вынужденных колебаний. К примеру, обработка хрупких материалов менее склонна к возникновению вибраций, несмотря на периодическое образование и скол элементов стружки. Резание вязких материалов, напротив, более склонно к вибрационному режиму, хотя образуется почти непрерывная сливная стружка. Очевидно, эти соображения указывают на несостоятельность гипотезы о вынужденном характере вибраций при резании.
Следует отметить, что при обработке металлов вынужденные колебания в той или иной степени всегда присутствуют, но их появление вызвано не процессом резания, а периодическими возмущающими силами вследствие дефектов передач, неуравновешенностью вращающихся частей и т.п. причинами. В связи с этим важно разграничивать колебания, возникающие вследствие физических особенностей процесса резания, и колебания, обусловленные конструктивными особенностями и погрешностями станка как машины для осуществления этого процесса. Представляется, что эти два явления суть не одно и то же, хотя процесс резания осуществляется на станке. При экспериментальном исследовании вибраций это разделение может быть весьма затруднительно, но при теоретическом анализе принципиально важно понимание того, какие колебания являются объектом исследования. До 1960-х гг. основное внимание исследователей было сосредоточено на вибрациях, обусловленных процессом резания.
Указанными авторами, начиная с Н.Л. Кайдановского и С.Э. Хайкина, была выдвинута гипотеза об автоколебательной природе вибраций при резании: их происхождение обусловлено не некоторой внешней вынуждающей силой, а свойствами самого процесса резания, который содержит источник энергии и регулирующий механизм, осуществляющий обратную связь с колебательной системой. Этим объясняется появление вибраций не только при совпадении частот, но и в достаточно широком диапазоне режимов резания. А.И. Кашириным были выполнены исследования автоколебаний при резании и получен ряд важных теоретических и экспериментальных результатов в отношении амплитуд, частот и физического объяснения вибраций. В частности, появление вибраций было связано с явлениями пластических деформаций в срезаемом металле, с имеющей максимум характеристикой силы резания от скорости. В целом фундаментальную работу [4], опирающуюся на физически ясные представления, можно признать большим вкладом в изучение колебаний при обработке резанием.
Примерно в то же время А.П. Соколовским [5,6] было предложено уравнение автоколебаний при резании (в радиальном направлении), основанное на эмпирическом представлении силы резания
 |
(1) |
где R – постоянная величина силы резания; r – член, выражающий зависимость силы от радиальных колебаний; B – действительная ширина режущей кромки; V – скорость резания; y – радиальные колебания; y – скорость радиальных колебаний; a, c – постоянные величины.
По физическому смыслу a, c являются коэффициентами жесткости третьей и четвертой составляющих сил в уравнении (1) – соответственно силы, возбуждающей колебания, и силы, ограничивающей колебания, когда их скорость превышает некоторое критическое значение. Член с кубической нелинейностью отражает явление снижения силы резания, а следовательно, снижения амплитуд при увеличении скорости.
Получающееся при этом уравнение автоколебаний на основе (1) имеет вид
 |
(2) |
где m – приведенная масса колеблющейся системы, h – коэффициент рассеивания энергии, k – коэффициент жесткости. Оно описывает снижение амплитуд A автоколебаний при увеличении скорости зависимостью
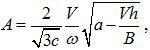
полученной методом Ван-дер-Поля, примененным к уравнению (2), причем при V=ab/h амплитуды уменьшаются до нуля. Это не совсем точно отражает действительность, однако более рациональной формы уравнения до сих пор не предложено. Оно было лишь усовершенствовано Л.К. Кучмой.
А.П. Соколовским был выявлен член ry, выражающий зависимость силы резания от радиальных колебаний и влияющий на обобщенную (приведенную) жесткость, что, в свою очередь, вносит поправку к частоте колебаний. Впрочем, этот фактор оказывается слабо влияющим, так что частоты при резании близки к собственным [4-7].
Уравнение А.П. Соколовского было первой попыткой анализа вибраций, основанной на феноменологическом описании силы резания, не вдаваясь в физическую сущность процесса, а лишь отражая его основные эмпирические закономерности. Несмотря на то, что точных аналитических зависимостей при резании вообще очень мало и приходится пользоваться эмпирическими формулами, все же можно признать, что объяснение явления с помощью возможно более простых и ясных частных эмпирических зависимостей вносит существенное развитие в понимание исследуемого вопроса. Так, в работе А.И. Каширина [4] изменение суммарной силы резания представлено как сумма частных изменений усилия из-за действия какого-либо одного физически ясного фактора: изменения силы трения стружки о резец, изменения углов резца, изменения мгновенного сечения, мгновенных режимов и т.д. Все это позволяет существенно улучшить анализ явления.
В этом направлении значительный вклад внес И.И. Ильницкий [7]. Он развил представление об автоколебательном характере вибраций и провел обстоятельный теоретический анализ для обоснования следующего предположения (выдвинутого А.П. Соколовским): основной причиной автоколебаний при резании является разница работ радиальной силы при врезании и отталкивании инструмента. Для этой цели был выполнен весьма трудоемкий и аккуратный расчет, подтверждающий исходную посылку – работа при врезании действительно не равна работе при отталкивании инструмента в колебательном движении. С одной стороны, это выявляет первопричину вибраций. Но поставим вопрос иначе, от противного. Предположим, что полная работа радиальной силы за период равна нулю. Из этого следует, что имеет место либо состояние покоя, либо установившиеся колебания с постоянной амплитудой. То есть разница работ свидетельствует о нарастании или затухании колебаний, но не об их происхождении, поскольку неизвестны причины этой разницы.
В связи с этим А.И. Кашириным ранее [4] было введено понятие первичного возмущения вибраций, происходящего из-за переработки поступающей энергии в энергию колебаний. Это явление обусловлено зависимостью силы трения о резец срезаемого металла и названо им «отрицательным трением». Подобное явление имеет место в таких известных автоколебательных системах, как ленточный тормоз или маятник Фруда, которые после выведения их из состояния покоя совершают незатухающие колебания. Основная причина таких автоколебаний – наличие локального минимума в зависимости силы трения от скорости. Проведенные эксперименты [4] показали, что вибрации при резании действительно наблюдались лишь в пределах спадающей ветви этой характеристики или вблизи нее.
В работе [7] И.И. Ильницкий, однако, не учитывает это явление и объясняет первичное возмущение вибраций любыми случайными воздействиями. В дальнейшем вибрации не затухают, т.к. имеет место вторичное возмущение, вызванное волнами на поверхности от предыдущих переходов («точение по следу»), причем на это указывается в работах [4-7].
Заметим, что не все исследователи поддержали автоколебательную природу вибраций. Так, В.Л. Вейц [8] считает, что в идеальной системе при любых режимах резец будет находиться в равновесии под действием силы резания и сил реакции, и только случайные воздействия могут вывести его из этого состояния. Однако представление о вибрациях как об автоколебаниях все же укрепилось. В этой связи можно отметить работы В.А. Кудинова [9], М.Е. Эльясберга [10] и других авторов.
Начиная с 1960-х гг. в исследовании колебаний при резании наблюдается поворот в сторону исследования динамики станков, т.е. объект интереса переносится с физического процесса на техническую систему. Динамика станков становится подразделом более общей научной дисциплины – динамики машин. Происходит постепенный отказ от изучения физической сущности динамики процесса резания и сосредоточение внимания на проработке вопросов проектирования станков с учетом динамических критериев. Задача, носящая изначально чисто прикладной характер – обеспечение рациональных условий обработки, во многом превращается из научно-исследовательской в конструкторскую. Исследования, направленные на разработку рациональной технологии, переходят в исследования, направленные на проектирование рациональных конструкций станков, обеспечивающих благоприятный динамический режим работы (в связи с этим возникает понятие динамического качества станков). Этот сдвиг в изучении вибраций при резании нигде не упоминается, но изменение даже самих названий научных трудов (можно сравнить [2-6] с [8-13]) свидетельствует о произошедшем повороте в исследованиях.
В классических трудах С.С. Кедрова [11], М.Л. Орликова [12] процесс резания является уже второстепенным явлением, а основное внимание сосредоточено на конструкции станка с точки зрения протекающих динамических процессов. Рассматриваются гармонические возмущающие силы, возникающие от неуравновешенности вращающихся деталей, а иногда и без объяснения их происхождения. При изучении указанных трудов можно заметить, что технологическим вопросам практически не уделяется внимания, поскольку работы рассчитаны на проектировщиков станков. По мнению автора, такой подход имеет коренной недостаток, состоящий в том, что отчасти пренебрегается именно той уникальной особенностью металлорежущих станков, благодаря которым они являются совершенно особой группой машин, - процессом резания. В результате динамика станков становится подразделом динамики машин, разрабатывающая и углубляющая частные вопросы, связанные с особенностями конструкции станков. Значительное влияние приобретает схематизация в исследованиях, берущая начало, вероятно, с В.А. Кудинова.
То направление, в котором пошло развитие динамики станков, в некоторой мере отстраняется от терминологии классической теории колебаний и насыщается узкоспециальными терминами, пригодными для конструкторов-проектировщиков станков, но иногда малопонятными для изучавших теорию колебаний, однако не знакомых с частными вопросами расчета и проектирования станков. Это явление присуще не только терминологии, но и методам изучения, что приводит к большей обособленности динамики станков.
Основные достижения в исследовании колебаний при резании, по мнению автора, относятся ко времени до 1950-х гг. В последние полвека в этом направлении не наблюдается мощных научных идей, способных продвинуть понимание динамических процессов на новый уровень. Такое впечатление складывается при сравнении научных работ середины и последней трети ХХ века. Тем не менее указанные работы последних десятилетий все же необходимо признать большим вкладом в развитие динамики станков и методом их проектирования с учетом динамических критериев.
В каком направлении пойдет развитие теоретических исследований рассматриваемого вопроса в ХХI веке? В настоящее время уже можно выделить несколько направлений. Основное из них – полный отказ от физического объяснения вибраций и уход в «имитационное моделирование» с упованием на готовые компьютерные программы. Этот подход можно назвать пользовательским, поскольку предполагает только использование готовых математических моделей (к слову, самому пользователю неизвестных) для решения конкретной прикладной задачи. Например, подбор рациональных конструкций деталей для обеспечения виброустойчивости, вычисление амплитуд или частот для уже известной конструкции и т.п. Нетрудно заметить, что фактически он означает сворачивание научных исследований и применение уже известных и разработанных методов для решения частных задач динамики станков. Естественно, что при таком подходе ни о каком развитии научной дисциплины речь не идет. Это напоминает накопление базы данных для разных вариантов конструкций, нагрузок и т.д.
Экспериментальные исследования в данном случае становятся инструментом подтверждения и оправдания применения готовых компьютерных программ, в чем можно убедиться на большинстве защищаемых диссертаций и публикуемых работ, выполненных в этом направлении.
Собственно аналитические исследования почти не ведутся, т.к. для их выполнения необходимо иметь разностороннюю математическую подготовку. В основе сего явления также лежит пользовательское отношение к науке, что противоречит самому ее духу.
Необходимо отметить, что три указанные тенденции характерны не только для исследования динамики станков или процесса резания, но и для других дисциплин, причем в разных странах, что позволяет сформулировать общемировой характер этих явлений в науке. Фактически свершившийся фундаментальный сдвиг в научном знании перевел традиционную науку в разновидность инновационной коммерческой деятельности. Однако не будем углубляться в подробности и уходить в сторону от рассматриваемого вопроса.
В последние годы все же можно выделить ряд работ, посвященных новым подходам в исследовании динамики резания. К ним прежде всего можно отнести работы Ю.Г. Кабалдина, опубликованные в различных номерах «Вестника машиностроения» с 2001 по 2006 гг., выполненные с использованием методов нелинейной динамики, теории фракталов, вейвлет-анализа и др. Заслуживает безусловного внимания динамическая модель процесса резания [14] с плавлением в зоне контакта инструмента с заготовкой, описываемая уравнениями Навье-Стокса. В работе [15] разработана математическая модель динамической устойчивости системы резания в виде нелинейного осциллятора с разрывными характеристиками и получена карта динамической устойчивости при разных режимах резания. Однако принятая модель периодичности силы резания от сколов элементов стружки, по мнению автора, несколько снижает ценность результатов. Тем не менее работы Ю.Г. Кабалдина заслуживают пристального внимания в силу аналитических методов исследования, способных к дальнейшему развитию.
Необходимо также указать на то, что в 2008 г. была опубликована [16] разработанная А.Л. Воронцовым, Н.М. Султан-Заде, А.Ю. Албагачиевым новая теория резания, находящаяся в соответствии с теоретическим аппаратом механики деформируемого твердого тела, в частности теории пластичности и механики разрушения. Примечательно, что она была разработана не резальщиками, а специалистами в области ОМД. Новая теория, возможно, способна пролить свет на некоторые вопросы динамики процесса резания, исходя из его физической сущности.