ОПРЕДЕЛЕНИЕ УПРУГОГО ОТЖАТИЯ ПРИ РЕЗАНИИ МЕТАЛЛА С УЧЕТОМ ДИНАМИКИ ПРОЦЕССА
Авторы: А.В. Пашинин, Е.А. ЧернышевУчебное заведение: каф. ТМ, ДонНТУ, г. Донецк, Украина
The paper presents description of the order of finding deformation in metal cutting by means of method, taking into account dynamics of cutting process.
Cutting, deformation, dynamics, vibrations.
При обработке резанием всегда возникает упругое отжатие в системе СПИД. Одним из методов определения отжатия при резании металлов является статический метод [1]. Этот метод заключается в нахождении отжатия как отношения действующей на тело силы к коэффициенту жесткости. Однако этот метод не учитывает динамики процесса резания, поэтому дает большую погрешность.
Целью данной статьи является определение упругого отжатия резца и заготовки как увода, т.е. с учетом динамики процесса резания. Для решения поставленной задачи рассмотрим токарную обработку и силы, действующие на резец и заготовку (рис.1). При этом резец и заготовку представим приведенными к точке А массами m1 и m2.
Составим уравнения динамики колебаний
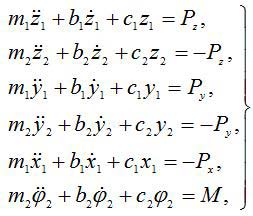 |
(1) |
где правая часть зависит от малых колебательных перемещений и их скоростей, причем М – крутящий момент, равный разности момента на двигателе и момента резания.
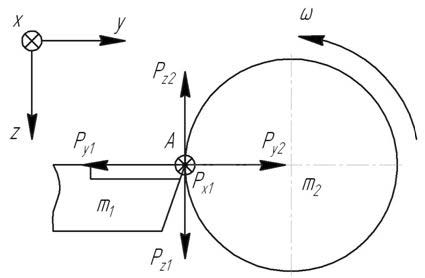
Рисунок 1 – Схема сил при токарной обработке внешней цилиндрической поверхности
Пренебрежем осевыми перемещениями заготовки, считая их малыми из-за большой жесткости шпинделя в том же направлении, обеспечиваемой упорными подшипниками.
В общем случае систему (1) можно решить описанным ниже образом.
Составляющие силы резания (P1, P2,…, Pn) представим зависимыми от малых перемещений (x1, x2,…, xn), и запишем систему (1) в виде:
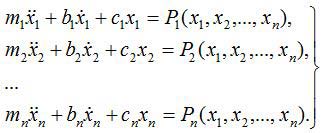 |
(2) |
Чтобы однозначно найти увод по всем координатам, линеаризуем правую часть системы (2). Пренебрежем инерционными и диссипативными членами, рассматривая только упругие. Это связано с тем, что координаты увода (особой точки) описываются условием экстремума потенциальной энергии, которая не зависит от скоростей и ускорений. В результате получим систему алгебраических уравнений:
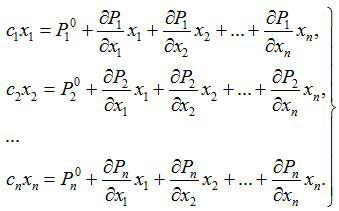 |
(3) |
Представим систему (3) в матричном виде:
где C - матрица коэффициентов жесткости; P0 - вектор составляющих сил резания без учета колебаний.

и найдем матрицу перемещений Х, характеризующую упругое отжатие в процессе резания:
Применение описанного метода позволяет учесть динамику процесса резания и избежать значительных погрешностей вычислений.