ТЕОРЕТИЧЕСКОЕ ОБНАРУЖЕНИЕ НЕОДНОЗНАЧНОСТИ СИЛ РЕЗАНИЯ В КОЛЕБАТЕЛЬНОМ ДВИЖЕНИИ ПРИ ТОЧЕНИИ
Авторы: А.В. Пашинин, Е.А. ЧернышевУчебное заведение: каф. ТМ, ДонНТУ, г. Донецк, Украина
При обработке точением возникают колебания, влияющие на параметры качества и точность получаемых размеров. Математическое описание этого процесса дает возможность прогнозировать такие режимы резания, которые позволили бы избежать неблагоприятных динамических условий при точении.
Целью данной работы является построение математической модели колебательной системы при продольном точении и выявление на ее основе экспериментально наблюдаемой разницы сил резания при врезании и отталкивании инструмента в колебательном движении.
Идеей, положенной в основу математической модели является следующее предположение: из-за колебательного движения резца и заготовки изменяются и мгновенные режимы резания, что обусловливает переменность силы резания, которую можно вычислить на основании эмпирической зависимости, если вместо номинальных режимов подставить их мгновенные значения.
При построении математической модели были приняты следующие допущения:
Резец и заготовка совершают малые колебательные перемещения (рис. 1).
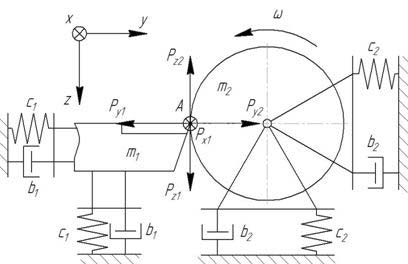
Рисунок 1 – Общая схема колебательной системы при точении (степени свободы, соответствующие осевым колебаниям резца и крутильным колебаниям заготовки, не показаны).
Эти перемещения и их скорости определяют мгновенные режимы резания, откло-няя их значения от номинальных (рис. 2).
Исходя из приведенных на рисунке 2 схем, были выведены зависимости мгновенных режимов резания от малых перемещений и их скоростей:

Рисунок 2 – Схемы для определения мгновенных значений глубины, скорости резания (а) и подачи (б)
где ω, t0, S0 - номинальные угловая скорость вращения заготовки, глубина резания и подача; V, t, S - фактические значения скорости, глубины резания и подачи; R0 - номинальный радиус заготовки.
Найденные зависимости были подставлены в эмпирические формулы для опреде-ления составляющих сил резания. Исходя из этого, была составлена система уравнений, описывающая колебания при точении:
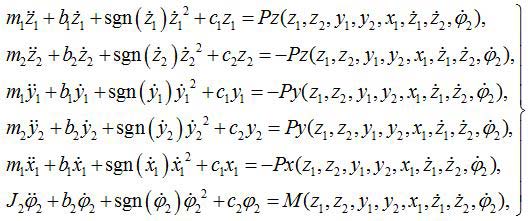
где m, b, c - приведенная масса, коэффициент диссипации и коэффициент жесткости резца (1) и заготовки (2); Px, Py, Pz - осевая, радиальная и тангенциальная составляющие усилия резания; M - крутящий момент, равный разности момента, развиваемого двигателем, и момента сил резания. В правой части в скобках стоят динамические переменные, от которых, согласно выражениям для фактических режимов, зависит сила резания.
В математическую модель был введен квадратичный диссипативный член для учета явления увеличения затухания с увеличением скорости движения.
Система уравнений решалась численно центрированным методом Эйлера с шагом интегрирования 10-5. Полученные результаты сравнивались с опытными данными, приведенными в работах А.И. Каширина [1] и И.С. Амосова [2], по двум критериям. Согласно результатам экспериментов, сила резания при отталкивании резца от заготовки больше, чем при врезании. А значит, сила резания не определяется однозначно относительным положением резца и заготовки. Этот же результат получен нами теоретически (рис. 3).

Рисунок 3 – Зависимость радиальной силы от относительных радиальных перемещений резца и заготовки
Обнаруженная нами разница сил при врезании и отталкивании инструмента в колебательном движении, давно известна из опытных данных [2]. А.П. Соколовским в 1940-х гг. была сделана попытка объяснить ее различными условиями резания при врезании и отталкивании [3]. Однако, как можно заметить, в разработанной математической модели физические условия резания нигде не фигурируют, они присутствуют лишь в виде эмпирических коэффициентов, описывающих количественную сторону – величину силы резания. Тем не менее, указанное явление обнаруживается. Это наводит на мысль, что разница сил объясняется не (только) особенностями процесса резания, а свойствами динамической системы, например нелинейностью затухания, на которую указывают различные авторы как на основной источник происхождения вибраций при резании. Последнее свойство в разработанной модели учтено квадратичным диссипативным членом, при отсутствии которого, к слову, установившийся колебательный режим не устанавливается. На эту особенность моделирования колебаний при резании указывает, в частности, Жарков [4]. По причине исключительной сложности рассматриваемого вопроса, не претендуя на окончательное суждение, оставляем его открытым.
Следует отметить характерное свойство исследуемой динамической системы. Изменение сил резания происходит по зависимости, близкой к синусоидальной. Это напоминает используемую во многих теоретических расчетах линейных систем синусоидальную вынуждающую силу, являющуюся причиной вынужденных колебаний. В данном же случае природа полученной силы принципиально иная, поскольку устанавливающиеся колебания удовлетворяют критериям автоколебаний. Ключевой особенностью силы резания является то, что зависимость ее изменения во времени заведомо неизвестна. В рассмотренном случае, при установлении одночастотного колебательного режима, изменение силы резания оказалось близким к синусоидальной зависимости. Однако динамическая система при этом является принципиально нелинейной и автономной, т.е. не зависящей явно от времени, поэтому амплитуда и частота изменения силы определяются внутренними свойствами системы в результате решения уравнений динамики. В качестве таких определяющих свойств мы считаем зависимости мгновенных режимов резания от колебательных перемещений и их скоростей.
Из вышеизложенного можно сделать вывод, что разработанная математическая модель не противоречит результатам экспериментов, так как радиальная сила при врезании больше, чем при отталкивании, т.е. не определяется однозначно относительными радиальными перемещениями резца и заготовки.