Оценка сил, действующих на фаске износа инструмента по задней поверхности

При чистовой обработке резанием от процессов, протекающих на фаске износа режущего инструмента (РИ), в большой степени зависят как факторы процесса резания (силовые, тепловые, деформационные), так и технологические параметры (шероховатость поверхност и, точность, наклеп поверхностного слоя, остаточные напряжения). При черновой обработке указанные процессы также существенно влияют на технологические параметры, хотя доля сил, действующих на фаске износа, в общем балансе сил незначительна. Влияние таких процессов на характеристики процесса резания во многом зависит от сил и напряжений, действующих на фаске износа. Однако приемлемых способов их определения до сих пор не найдено.

Это объясняется, в частности, техническими трудностями экспериментального исследования сил, действующих на фаске износа. Известные экспериментальные методы (метод отрезного резца [1], экстраполяция на нулевую толщину срезаемого слоя [2], моделирование на поляризационной установке [3] и др.) позволяют получить лишь приближенные результаты. Решение задачи усложняется и тем, что контакт РИ с заготовкой по фаске износа в связи с непрерывным изнашиванием имеет случайный характер, поэтому воз можна лишь вероятностная оценка сил и напряжений. Методы, основанные на имитации фаски износа путем специальной заточки РИ (создание фаски с нулевым задним углом) в данном случае непригодны, так как искусственно созданная фа ска существенно отличается по геометрии от естественной фаски износа.

В связи с указанным решающее значение приобретают аналитические и численные методы. При этом полнота и точность решения определяются степенью приближения используемой модели к реальному процессу. Такая модель должна в первую очередь отражать физическую природу возникновения контактных нагрузок на фаске износа инструмента. Известные решения [2 и 4] не отражают основной механизм возникновения сил на фаске износа и содержат множество неизвестных факторов, поэтому для инженерных расчетов они непригодны.

Решения [2 и 4], основанные на контактной задаче теории упругости [5], отражают лишь краевые эффекты при вдавливании абсолютно жесткого пуансона, моделирующего лезвие РИ, в упругое полупространство. Исходным при этом является положение о том, что в точке отрыва

стружки от заготовки на поверхности скругления режущей кромки обрабатываемый материал (как не переходящий в стружку, так и образующий стружку у передней поверхности РИ) находится в состоянии пластичности. Однако это условие не следует считать обязательным, так как в данной точке обрабатываемый материал разделяется и нарушается связь между стружкой и телом заготовки. Не учитывается также глубина вдавливания пуансона, которая главным образом и определяет силу вдавливания [6].

Исходя из краевого эффекта была построена )шора распределения нормальных контактных нагрузок на фаске износа [4 и др.], согласно которой напряжения в крайних точках по ширине фаски значительно превышают напряжения в средних точках. Для РИ такая эпюра маловероятна, гак как он подвергается непрерывному изнашиванию, формирующему геометрию фаски. Краевые участки фаски вследствие больших контактных напряжений, возникающих в начальный период ее образования, изнашиваются интенсивнее упругих. В результате распределение напряжений m фаске выравнивается. Поэтому наиболее вероятно равномерное распределение контактных напряжений по ширине фаски износа.

В работе [3] сделан вывод о том, что силы, действующие на фаске износа, порождаются силами стружкообразования. Последние действуют на средней поверхности РИ и вызывают подъем поверхности резания сзади режущей кромки, в результате чего создается давление на фаску из- оса. Однако этот вывод не согласуется с экспериментальными данными [6 и 7]. В работе [7] приведены результаты измерения силы на фаске и юса в момент прекращения образования стружки при резании с непрерывно уменьшающейся толщиной срезаемого слоя. Эти данные утверждают, что силы на фаске износа существуют даже тогда, когда отсутствуют силы стружкообразования

Ниже предложена зависимость для расчета сил, действующих на фаске износа, полученная на основе решения контактной задачи теории упругости о вдавливании пуансона эллиптической формы в плане в упругое полупространство J при следующих допущениях.

1. Эпюра распределения контактных нормальных напряжений по ширине фаски износа принята равномерной.
2. Упругие деформации лезвия РИ и силы трения на фаске износа не влияют на эпюру распределения контактных нормальных напряжений.
3. Силы стружкообразования не оказывают влияния на контактные процессы и нагрузки на фаске износа.
4. Передняя и задняя поверхности лезвия РИ сопрягаются по круговой цилиндрической поверхности.
5. Коэффициент трения на указанной поверхности сопряжения соответствует температуре резания на передней поверхности у режущей кромки.
6. Рассматриваются режимы чистовой обработки, при которых наростообразование отсутствует.

Рис. 1. Геометрия области контакта РИ с заготовкой по фаске износа

В качестве основной причины возникновения сил на фаске износа принята упругая деформация обрабатываемого материала, обусловленная скруглением лезвия РИ по некоторому радиусу г (рис. 1). Лезвие не полностью преобразует в стружку номинальный срезаемый слой толщиной а: часть его толщиной ас переходит в стружку, а другая часть толщиной H не срезается. При движении лезвия поверхность AM среза вследствие упругой деформации материала заготовки посте-пенно опускается на величину И и обрабатываемая заготовка оказывает давление на фаску износа шириной h3. Поэтому лезвие можно рассматривать как пуансон, вдавленный в упругое полупространство на глубину И. Последнюю можно определить, если принять, что в точке М, где срезаемый слой разделяется, касательное напряжение t совпадает по направлению с вектором скорости V резания и составляет с результирующим напряжением сигма угол 45° (напряжение сигма порождается результирующей силой Р, имеющей нормальную N и касательную У составляющие). При этом условии справедлива следующая зависимость:

Аналогичная зависимость для расчета H, но из иных предпосылок получена в работе [9], что подтверждает справедливость формулы (1).

Для определения нормальной силы Q, действующей на фаске износа шириной h3 и длиной, равной ширине b срезаемого слоя, используем зависимость [6], согласно которой сила вдавливания пуансона с основанием произвольной формы в упругое полупространство заключается в следующих пределах:

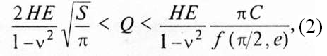
В качестве вероятной оценки нормальной силы принимаем среднее арифметическое значение из верхнего и нижнего пределов [см. выражение (2)]:

Зависимость (3) не учитывает силы, действующие на лезвие на участке ML его скруглення (см. рис. 1) и на участке BD выхода, которые при малых значениях заднего угла a и радиуса r могут быть достаточно велики. Для их определения рассматривали треугольные эпюры распределения нормальных напряжений на участках ML и BD.

Среднее нормальное напряжение на фаске из носа q = Q/(bh3). Расчет по этой зависимости показывает, что контакт инструмента по фаске износа с заготовкой чаще всего упругий. Однако он может быть и пластическим, если на участке скругления лезвия нормальные напряжения при переходе от точки M к точке L возрастают от нуля до значения qn, вызывающего пластическую деформацию обрабатываемого материала. В случае пластического контакта, когда q > qu и величина упругого восстановления поверхности резания Н' больше чем H (см. рис. 1), Q= qnb (h3 + 0,5L).

Результаты расчета по приведенным выше зависимостям согласуются с известными данными [2 и 8]. По этим зависимостям построены графики (рис. 2); условия их построения см. в таблице. Анализ графиков позволяет сделать ряд выводов.

1. Наибольшее влияние на силу Q оказывает коэффициент мю трения на поверхности скруглення лезвия: с его увеличением эта сила интенсивно уменьшается и при мю = 1 перестает действовать (Q = 0)
2. Увеличение твердости НВ обрабатываемого материала приводит к возрастанию силы Q.
3. Влияние заднего угла а на силу Q подобно влиянию коэффициента трения, однако выражено не так явно.
4. Увеличение ширины b срезаемого слоя приводит к возрастанию силы Q, однако темп роста силы отстает от темпа увеличения ширины срезаемого слоя.
5. Увеличение ширины h3 фаски износа вызывает существенный рост силы Q как из-за увеличения площади поверхности фаски, так и вследствие увеличения радиуса скругления режущей кромки. Поэтому темп роста силы Q превышает темп роста ширины фаски износа.

Список использованной литературы

1. Клуши» М.И., Гордон М.Б. Силы трения по передней поверхности инструментов и их влияние на процесс резания металлов // Вестник машиностроения. — 1952. — № 3.
2. Зорев Н.Н. Вопросы механики процесса резания металлов. — М.: Машгиз, 1956. — 367 с.
3. Кравченко Б.А. Силы, остаточные напряжения и трение при резании металлов. — Куйбышев: Кн. изд-во, 1962. — 179 с.
4. Стрельцов В.Л. Исследование процесса контактирования задней поверхности режущего инструмента с обрабатываемой поверхностью // Вестник машиностроения. — 2001. — № 10 — С. 38-41.
5.Штаерман И.Я. Контактная задача теории упругости. — М.: Гос. изд-во техн. тсор. лит., 1949. — 270 с.
6.Галии Л.А. Контактные задачи теории упругости и вязко-упругости. — М.: Наука, 1980. — 304 с.
7.Иткин М.Э. Исследование сил, действующих на грани резца // Обрабатываемость жаропрочных и титановых сплавов: Сб. трудов всесоюз. межвуз. конф. — Куйбышев: Кн. изд-во, 1962. - С. 292-305.
8.ГІолетика М.Ф. Контактные нагрузки на режущих поверхностях инструмента. — М.: Машиностроение, 1969. — 150 с
9.Крагельский И.В. Трение и износ. — М.: Машиностроение, 1968. - 480 с.
10. Железнов Г.С. Прогнозирование величины радиуса скругления режущей кромки инструмента // СТИН. — 2001. - № 7. - С. 11-14.
11. Саверин М.М. Контактная прочность материала в условиях одновременного действия нормальной и касательной нагрузок. — М.: Машгиз, 1946. — 245 с.