Применение метода конечных элементов при расчете сверла на кручение

Сверло для обработки глубоких отверстий малого диаметра — наиболее слабое звено технологической системы, ограничивающее производительность обработки. Наибольшую трудность представляет сверление глубоких отверстий в вязких материалах из-за возможного пакетирования и защемления сливной стружки в стружечных канавках сверла. Это приводит к появлению задиров на поверхности отверстий, а иногда к поломке сверла.

Для стабильной работы станка и увеличения производительности обработки применяют механическое или кинематическое дробление стружки и адаптивное глубокое сверление [1]. Эти же цели могут быть достигнуты повышением жесткости стебля сверла. Однако в ряде случаев теоретическими методами крайне сложно оценить напряженно-деформированное состояние сверла, имеющего, как правило, каналы для подвода СОЖ и сложный профиль.

В таких случаях весьма эффективны численные методы расчета и, в частности, метод конечных элементов (МКЭ). Являясь приближенным методом решения задач, МКЭ может обеспечивать приемлемую точность расчетов при соответствующем разбиении рассматриваемой области инструмента на конечные элементы (КЭ). Значительная трудоемкость расчетов связана с составлением вычислительных программ, но решение задач существенно облегчается, поскольку алгоритм МКЭ является универсальным и позволяет использовать ЭВМ [2 и 3].

Рассмотрим возможную последовательность решения плоской (двумерной) задачи расчета на кручение стебля сверла с прямыми стружечными канавками [4] при разбиении его поперечного сечения (рис. a) на КЭ треугольной формы. С учетом симметрии профиля сечения рассматривается лишь 1/4 его часть (рис. б)

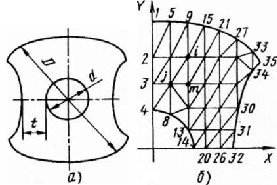
Рисунок 1 – Поперечное сечение сперла для глубокого сверления (а) и разбиение 1/4 его сечения на конечные элементы (б)

Примем постоянными и известными модуль G сдвига материала сверла (МПа), относительный угол {тета} закручивания (отнесенный к длине 1000 мм) и размеры D, d и t (см. рис. а) поперечного сечения сверла. Неизвестными считаем крутящий момент M (Нм), обеспечивающий заданный угол закручивания, и касательные напряжения {тау} (МПа) в поперечном сечении.

Для решения задачи используем мембранную аналогию Прандтля [2 и 5], согласно которой вводимую функцию напряжений можно представить как некоторую упругую поверхность, охватывающую поперечное сечение стержня. Крутящий момент пропорционален объему, охватываемому этой поверхностью, а касательные напряжения в произвольной точке сечения.

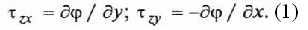
Дифференциальное уравнение для функции напряжений имеет вид

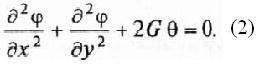
Граничными являются следующие условия: на наружном контуре {фи} = 0; на внутреннем контуре ? = const. Поскольку в стебле сверла имеется отверстие для подачи СОЖ, необходимо часть воображаемой мембраны заменить горизонтальной неупругой поверхностью (пластиной) [5].

Площадь сечения сложного профиля определяется как сумма площадей КЭ, на которые разбивается сечение. В связи с аппроксимацией функции напряжений значение крутящего момента, полученное в результате численного эксперимента, меньше, чем при точном расчете; при более мелкой сетке разбиения точность расчета повышается.

Крутильная жесткость стебля сверла постоянного сечения С = Mс / {тета} = GLk, где Lк — геометрическая характеристика крутильной жесткости сечения.

Стебель сверла можно рассчитать на продольный изгиб с помощью МКЭ, если момент инерции его сечения относительно оси К представить как сумму моментов инерции всех КЭ.

Использование ЭВМ значительно сокращает трудоемкость расчетов, позволяет оперативно анализировать напряженное состояние сверла сложного сечения, сравнивать жесткость сверл разной конструкции и оптимизировать процесс проектирования.

Список использованной литературы

1. Обработка глубоких отверстий / Н.Ф.Уткин, Ю.И.Кня- жев, С.К.Плужников и др.; Под общ. ред. Н.Ф.Уткина. — Л.Машиностроение, 1988. — 269 с .
2. Сегерлинд Л. Применение метода конечных элементов. - М: Мир, 1979. - 388 с.
3. Розин Л.А. Задачи теории упругости и численные методы и у мнения. - Спб.: СпбГТУ, 1998. - 531 с.
4. Прогрессивные режущие инструменты и режимы резания металлов: Справочник / Под обш. ред. В.И.Баранникова. — М.: Машиностроение, 1990. — 400 с.
5. Тимошенко С.П., Гудьер Дж. Теория упругости / Под ред. Г.С.Шапиро. - М.: Наука, 1979. - 531 с. — 245 с.