Авторы: Marcus Windisch, Gerhard Fettweis

Автор перевода: Абраменко А.А

Источник: Control, Communications and Signal Processing, 2004. First International Symposium

Аннотация

Проблема подавления зеркального канала присуща приемникам всех архитектур. Одним из преимуществ приемника с низкой промежуточной частотой (ПЧ) является то, что подавление зеркального канала реализуется за счет I/Q обработки сигналов вместо использования аналоговых фильтров, что делает его гибким и экономически эффективным. Однако неизбежный дисбаланс между ветками I и Q ограничивает степень подавления зеркального канала. В данной статье предлагается новая схема компенсации I/Q дисбаланса, в которой неизвестные параметры дисбаланса определяются по средствам цифровой обработки без необходимости использования обучающих или калибровочных сигналов. Основанная на этих оценках компенсация является эффективной и средний уровень зеркального канала никогда не превысит заранее определенного максимального значения.

Введение

Приемник с I/Q обработкой сигналов, такой как приемник прямого преобразования или приемник с низкой промежуточной частотой является хорошим выбором для требующих постоянной перенастройки стандартов радиосвязи. Отныне не требуется фильтра для подавления зеркального канала, вместо этого используется дешевая и гибкая в настройках аналоговая часть. В теории, бесконечное подавление зеркального канала может быть достигнуто если используемый комплексный гетеродин имеет одинакновые амплитуды сигналов при разности фаз равной 90 градусов. Однако на практике такого соотношения между I/Q составляющими никогда не удается достичь, поэтому подавление зеркального канала ограничено. Реальные цифры для технологий сегодняшнего дня – это подавление зеркального канала на уровне 30–40 дБ при амплитудном небалансе 1–2 % и фазовом небалансе 1–2 градуса.

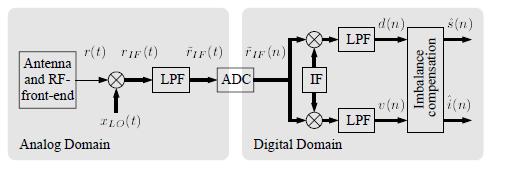
Рисунок 1. – Структура приемника с низкой ПЧ и цифровой компенсацией дисбаланса

В литературе рассматривается несколько схем для цифровой компенсации дисбаланса. Наиболее простая – это оценка параметров дисбаланса с использованием калибровочного сигнала [2]. Более продвинутые методы используют общие алгоритмы метода слепого разделения источников, такие как Interference Cancellation (IC) и Blind Source Separation (BSS). Несмотря на то, что эти методы позволяют достичь значительных результатов при определенных условиях приема, им присущи определенные недостатки, такие как утечка сигнала в IC-подходах и значительная вычислительная сложность в подходах, использующих BSS. Данная статья представляет BSS подход, который объединяет преимущества описанных выше методов.

Математическая модель дисбаланса в приемнике с низкой ПЧ

Принцип работы приемника с низкой ПЧ заключается в перенесении сигнала передающегося на частоте f_RF=f_LO+f_IF в область нулевой ПЧ в результате двух последовательных преобразований частоты, первое из которых сдвигает сигнал на f_LO с помощью квадратурного гетеродина аналоговой части, а второе – на f_IF с помощью цифрового гетеродина. Вещественный сигнал радиочастоты перед понижением частоты может быть представлен следующим образом:

Рисунок 2. – Структура приемника с низкой ПЧ и цифровой компенсацией дисбаланса

Комплексный сигнал z(t)=s(t)e^+j2pif_LOt +i^*(t)e^-j2pif_LOt состоит из полезного сигнала и потенциального (сигнала зеркального канала). Оба сигнала s(t) и i(t) являются полосовыми с шириной спектра 2f_IF. Любые факторы, которые влияют на дисбаланс учтены в данной модели.

Неидеальное понижение частоты имитируется комплекным гетеродином, который описывается функцией времени x_LO(t)=cos(2*pi*f_IF*t)-j*g*sin(2*pi*f_IF*t +φ), где параметр g характеризует амплитудный дисбаланс а φ – фазовый. Следуя выкладкам, изложенным в [4] можно записать параметры, характеризующие дисбаланс:

С учетом этого можно записать функцию времени комплексного гетеродина, используя приведенные соотношения:

В соответствии с данной моделью сигнал на промежуточной частоте формализуется следующим образом:

Поскольку дальнейшая обработка сигнала происходить в цифровой форме необходимо заменить непрерывные аналоговые сигналы их дискретными эквивалентами s(n), i(n), r_IF(n). Считается, что цифровое комплексное преобразование частоты является идеальным, поэтому его результат может быть представлен следующим образом:

На практике структура сигнала d(n) такова, что в ней преобладает принимаемый сигнал s(n), но в силу наличия дисбаланса, он интерферирует с сигналом зеркального канала i(n).

Теперь рассмотрим другое преобразование частоты:

В данном случае доминирует сигнал зеркального канала, в тоже время он подвержен интерференции со стороны основного сигнала. Необходимо отметить, что понятия основного сигнала и зеркального канала весьма двусмысленны, и зависят от того, относительно какого сигнала ведется прием.

Компенсация дисбаланса

Важным свойством матрицы K является то, что ее четыре комплексных элемента завимы, поэтому она имеет всего две степени свободы вместо восьми. Этот факт может быть использован для нахождения неизвестных параметров дисбланса K₁ и K₂. Предлагаемый в данной статье метод предполагает оценивание математических ожиданий двух статистик, первая из которых носит название взаимная корелляция E{d(n)v(n)}, а вторая – квадрат суммы сигналов E{|d(n)+v*(n)|²}, где E означает матожидание.

Анализируя выражение для кросс-корелляции

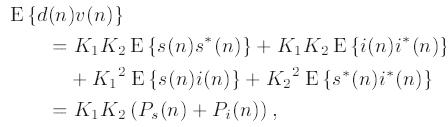
можно заметить, что P_s(n)=E{s(n)s*(n)} и P_i(n)=E{i(n)i*(n)} определяют энергию исходных сигналов s(n) и i*(n) соответсвенно. С учетом принятого допущения, что сигналы s(n) и i(n) некореллируемы, можно утверждать, что E{s(n)i*(n)}=0. На практике, однако, некоторая корелляция присутствует, но в рамках данного подхода мы считаем ее пренебрежительно малой, поскольку рассматривается идеальный случай.

С другой стороны мы можем записать:

Теперь можно формализовать квадрат суммы сигналов d(n) и v*(n):

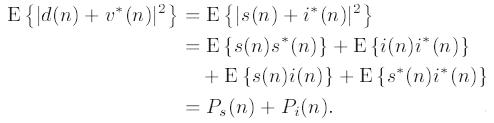
Теперь основываясь на полученных выше выражениях можно получить основное равенство, на котором основана работа предложенного алгоритма:

Произведение K₁ и K₂ содержит достаточно информации, чтобы получить из них неизвестные параметры дисбаланса. Произведение параметров K₁ и K₂ может с другой стороны преобразовано как 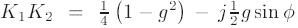. Отсюда могут быть получены следующие соотношения:

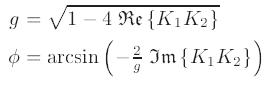
Для того, чтобы предложенный алгоритм мог быть использован на практике предлагается заменить математическое ожидание средним значением N отсчетов сигнала.

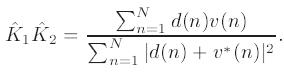
Искомая корректирующая матрица определяется следующим образом

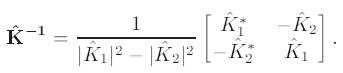
Для компенсации дисбаланса необходимо воспользоваться корректрирующей матрицей. Структрура самого компенсатора приведена на рис.3.

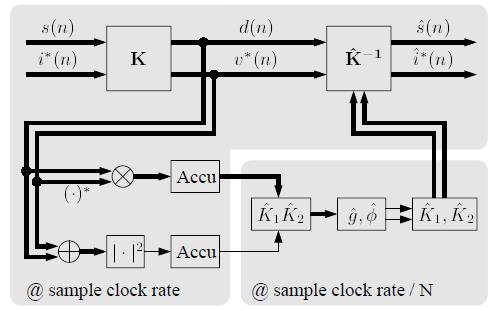
Рисунок 3. – Структура предложенного алгоритма оценки и компенсации I/Q-дисбаланса

Как видно из рисунка 3, для того чтобы выполнить оценку и компенсацию необходимо всего 8 вещественных сложений и 6 вещественных умножений на частоте дискретизации. Наиболее вычислительно емкой является процедура вычисления корректирующей матрицы. Она может быть осуществлена на более низкой скорости, зависящей от размера блока N.

Результаты моделирования

Возможности предложенного алгоритма были оценены в ходе моделирования, ипользуя модель полосового радиосигнала, изображенную на рис.3. Для рассмотрения наиболее общего случая сигналы s(n) i*(n) были сгенерированы как стационарно-независимые Гауссовы случайные процессы с мощностями P_s и P_i соответственно.

В качестве критерия принимается коэффициент подавления зеркального канала, равный отношению квадратов коэффициентов K₂ и K₁, скорректированный на отношение мощности сигналов зеркального и основного каналов.

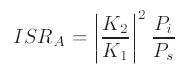
Также следует отметить, что коэффициент подавления зеркального канала может быть расчитан на основе параметров элементов корректирующей матрицы

В ходе моделирования производилось изменение размера блока N. Для каждого настройки моделирования было смоделировано 1000 независимых реализаций сигналов и вычислений коэффициента ISR, на основе результирующих параметров дисбаланса.

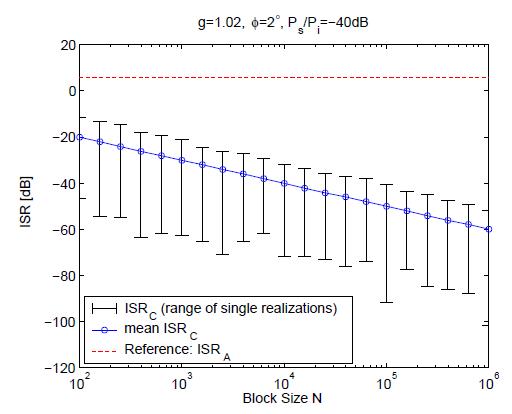
Рисунок 4. – Зависимость среднего значения ISR от размера блока N

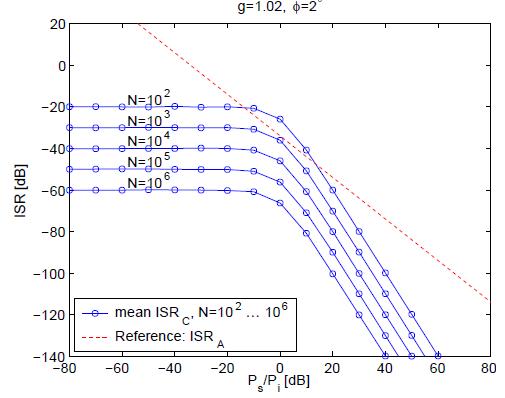
Рисунок 5. – Зависимость среднего значения ISR от соотношения синалов основного и зеркального каналов при разных N

Как видно из рис.5, среднее значение ISR никогда не превысит некоторого конечного значения вне зависимости от мощности сигнала зеркального канала.

Заключение

Предложен новый алгоритм компенсации дисбаланса для приемников с низкой промежуточной частотой, который способен оценить неизвестные параметры дисбаланса без использования обучающих или калибровочных последовательностей. Возможности предложенного подхода были оценены в ходе имитационного моделирования. Важно отметить, что среднее значение отношения основного сигнала и сигнала зеркального канала после компенсации является ограниченным сверху и не зависит от мощности сигнала зеркального канала. Более того, для достижения требуемого результата, значение ISR может быть скорректировано на основе размера блока обработки N.

Перечень ссылок

[1] Jan Crols and Michiel S. J. Steyaert, “Low-IF Topologies for High-Performance Analog Front Ends of Fully Integrated Receivers,” IEEE Trans. Circuits Syst. II, vol. 45, no. 3, pp. 269–282, Mar. 1998.

[2] Jack P. F. Glas, “Digital I/Q imbalance compensation in a Low-IF receiver,” in IEEE Global Communications Conference, Nov. 1998, vol. 3, pp. 1461–1466.

[3] Li Yu and W. Martin Snelgrove, “A Novel Adaptive Mismatch Cancellation System for Quadrature IF Radio Receivers,” IEEE Trans. Circuits Syst. II, vol. 46, no. 6, pp. 789–801, June 1999.

[4] Mikko Valkama, Markku Renfors, and Visa Koivunen, “Advanced methods for I/Q imbalance compensation in communication receivers,” IEEE Trans. Signal Processing, vol. 49, Oct. 2001.

[5] Marcus Windisch and Gerhard Fettweis, “Performance Analysis for Blind I/Q Imbalance Compensation in Low-IF Receivers,” in Proc. First International Symposium on Control, Communications and Signal Processing, submitted, Hammamet, Tunisia, Mar. 2004.