При управлении сложными объектами, функционирующими в условиях нестационарности, широкое применение нашли адаптивные регуляторы, реализующие типовые ПИ– или ПИД–законы регулирования. Адаптивные контроллеры зарубежных и отечественных производителей: Ремиконт, Овен, Сименс, Микрол и т.д., как правило, реализуют метод Зиглера–Николса [1]. Следует отметить, что данный метод предполагает вывод объекта в область автоколебаний, за счет перехода на П–закон и грубого варьирования коэффициента усиления К_р. Однако, значительный ряд технологических процессов по условиям эксплуатации не допускают автоколебательного режима. Таким образом, задача нахождения оптимального метода адаптации остается открытой.

Вместе с тем, в последнее время широкую популярность находят нечеткие модели и алгоритмы управления [2, 3, 5]. Известно, что нечеткое управление основано на использовании не столько аналитических или теоретических моделей, сколько на практическом применении знаний квалифицированных специалистов, представленных в форме лингвистических баз правил. Нечеткое управление эффективно в случаях недетерминированности параметров объектов, когда существует определенный опыт экспертов по управлению и настройке автоматизированной системы регулирования (АСР). Теория нечеткой логики позволяет использовать знания специалистов – наладчиков с целью улучшения процессов управления и оказания помощи (супервизорный режим) по настройке типовых регуляторов. Исходя из вышесказанного, задача создания метода адаптации ПИД–регулятора, реализующего опыт наладчиков, становится актуальной.

Целью статьи является разработка нечеткой экспертной системы, определяющей оптимальные настройки ПИД–регулятора, для его адаптации к объекту управления, и ее апробация в пакете Matlab (Simulink). Разобьем научную задачу на ряд этапов. На первом этапе определим структуру адаптивной АСР (рис.1):

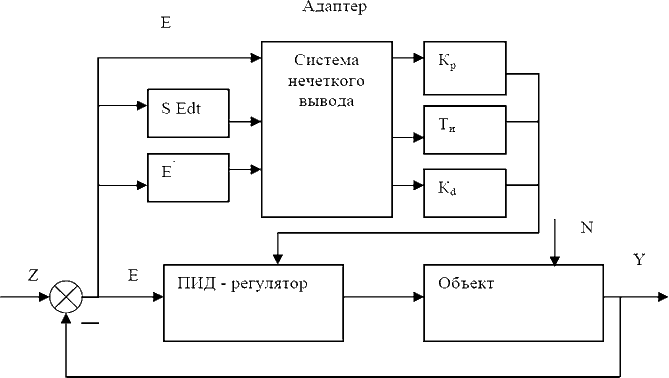
Рисунок 1 – Структура адаптивного нечеткого управления

где Е – ошибка; Z – задание; Y – выходное значение; N – возмущение; Кр, Ти, Кd – настройки ПИД–регулятора.

На втором этапе в программе Matlab (FLT) производится создание системы нечеткого вывода или адаптера (рис.2)

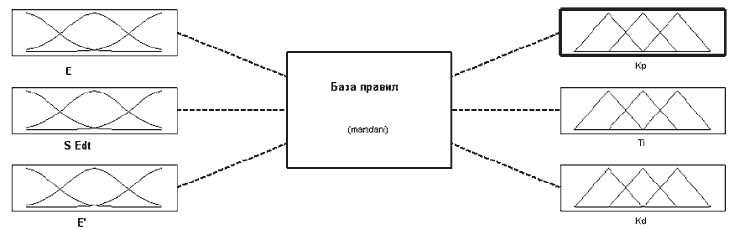
Рисунок 2 – Графический интерфейс редактора FIS

На третьем этапе проводится фаззификация входных и выходных лингвистических переменных (ЛП). Фаззификация входных значений (ошибки регулирования (Е), ее интеграла и производной) производится согласно рекомендациям [4]. Графики функций принадлежности входных ЛП представлены на рис. 3 – 5.

Функцию принадлежности Z‑вида, представляющую терм – «отрицательная ошибка otr » можно представить в виде: f_z (x, − 0.6, − 0.1) = [ 1, x < − 0.6; − 0.1 – x / 0.5; 0, − 0.1 < x].

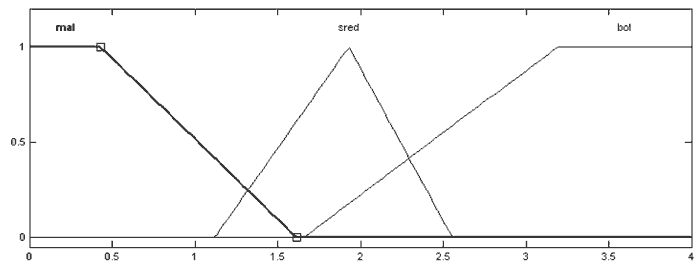
Рисунок 4 — Функции принадлежности ЛП «интеграл ошибки»: mal — маленький, sred — средний, bol – большой

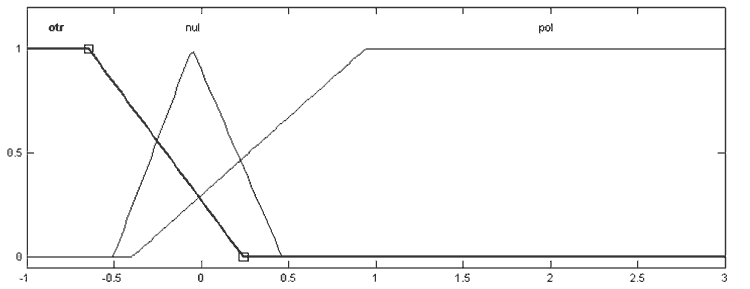
Рисунок 5 – Функции принадлежности ЛП «производная ошибки»

Этап фаззификации выходных ЛП «настройки ПИД–регулятора» проведен с учетом рекомендаций [4,5] и представлен на рис. 6.

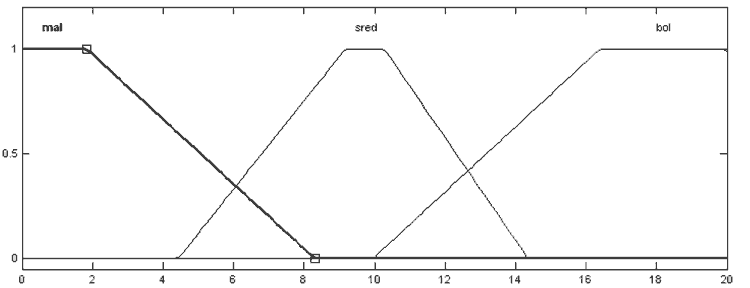
Рисунок 6 — Функции принадлежности ЛП «коэффициент усиления Кр»: mal — маленький, sred — среднний, bol – большой

Функции принадлежности ЛП «Т_и» и «К_d» также отображаются Z и S – образными графическими видами. Следует отметить, что Ти лежит на универсуме [0–5], а К_d = [0–15]. Четвертый этап заключается в создании базы правил вида «ЕСЛИ …ТО». Исходя из рекомендаций из специализированной литературы [5], проведенных экспериментов в редакторе FLT, а также опыта экспертов-наладчиков систем автоматизации, предлагаются следующие правила: ЕСЛИ «ошибка есть отрицательная» И «интеграл ошибки есть маленький» И «производная ошибки есть отрицательная» ТО «К_р есть большой», «Т_и есть большой», «К_d есть большой» и т.д. (рис. 7)

Рисунок 7 – Фрагмент базы правил

На следующем этапе проводится компьютерное апробирование нечеткой модели. В первоначальном эксперименте использовалась АСР с ПИД-регулятором, функционирующем по каналу задания Z=1, при влиянии на объект канала возмущения при этом: W_об(S) = 2.5/(5S²+3S+1); W_N(S) = 0.5/(5S+1). Настройка регулятора проводилась методом Зиглера–Николса. Значения настроек равны К_р = 1.3; Т_d = 0.15; К_d = 10.3, а переходный процесс удовлетворяет основным показателям качества. Предположим, что в связи с неопределенностью условий эксплуатации объекта, произошло изменение значений ключевых параметров такового. Например, W_об(S) = 2.5/(15S² +2S+1); W_N(S) = 3.5/(15S+1). При известных настройках регулятора, переходный процесс с новыми значениями передаточных функций обладает перерегулированием G = 80%, что недопустимо (рис.8).

Рисунок 8 – Переходный процесс по каналу задания

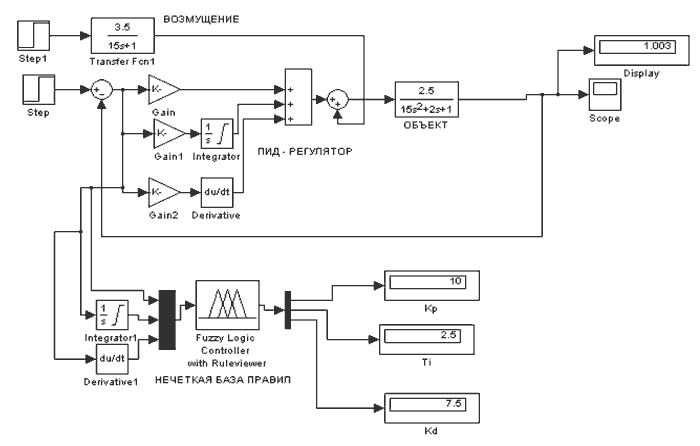
Рисунок 9 – Экспериментальная схема, выполненная в программе (Simulink)

Таким образом, необходима временная остановка сложного технологического процесса и перенастройка значений настроек ПИД-регулятора. Произведем проверку нечеткого адаптера при известных условиях (рис.9). Нечеткая система выдала следующие результаты: К_р = 10; Т_и = 2.5; К_d = 7.5, а переходный процесс регулирования при данных настройках для ПИД-регулятора показан на рис.10.

Рисунок 10 – Переходный процесс, полученный при адаптивных настройках

Как видно из рис.10, перерегулирование G не превышает 30%, что допустимо, а время регулирования T_р уменьшилось по сравнению с предыдущем на 30 секунд. Результат работы нечеткого адаптера в программе Matlab (FTL) показан на рис.11.

Рисунок 11 – Результат работы нечеткого адаптера

Таким образом, использование нечетких адаптивных ПИД-регуляторов позволит эффективно управлять технологическими процессами без их остановов, а дальнейшее введение нейрокомпьютера может привести к самообучающейся адаптации по определению оптимальных настроек без корректировки базы правил.

Список использованной литературы

1. Дьяконов В.П. Simulink 5/6/7 Самоучитель.– М.:ДМК, 2008 – 781с..
2. Леоненков А. Ю. Нечеткое моделирование в среде Matlab и fuzzyTech. – С. – Птб.: БХВ, 2003. – 720 с..
3. Мелихов А.Н. и др. Ситуационные советующие системы с нечеткой логикой. – М.: Наука, 1990. – 272 с.. – 216с.
4. Ротач В.Я., Клюев А.С. Автоматизация настройки систем управления. М.: Энергоиздат, 1984 – 272 с..
5. Алиев Р.А., Церковный А.Э., Мамедова Г.А. Управление производством при нечеткой исходной информации. М.: Энергоиздат. 1991. – 234 с..