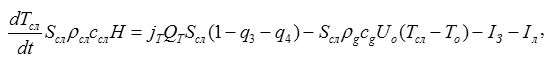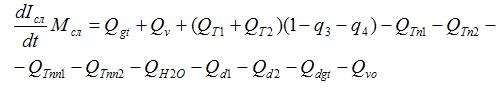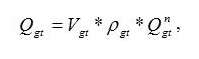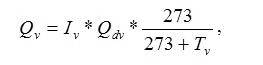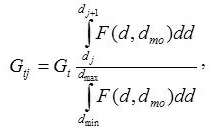Назад в библиотеку
Исследование динамических свойств котельной установки низкотемпературного кипящего слоя для задач автоматического управления
Автор: Петренко Е.П.
Источник: Севергеоэкотех–2011. Сборник научных работ XII Международной молодежной научной конференциии – Ухта, УГТУ, 2011. – 440 с.
В настоящее время весьма актуальна проблема экономии энергетических ресурсов,
и одним из вариантов ее решения является использование нетрадиционных технологий, например таких,
как сжигание высокозольного твердого топлива в низкотемпературном кипящем слое (НТКС).
В частности, топка НТКС может быть использована как источник теплоносителя для автономного газовоздушного
воздухоподогревателя, предназначенного для обогрева ствола в зимний период. Однако одним из сдерживающих факторов
внедрения подобных установок является несовершенство системы автоматизированного управления данным технологическим
объектом, которая представляет собой ряд обособленных контуров управления, выполненных на основе устаревших
регуляторов типа Р-25. Одним из необходимых условий для синтеза качественно новой системы автоматизации
является установление математических зависимостей топки кипящего слоя.
К настоящему времени имеется значительное количество работ, посвященных данной тематике. Обзор и анализ
исследований, выполненных до 1989 года [1], а также более поздних работ [2, 3, 4] позволили выявить следующие
недостатки существующих математических моделей:
- предполагается известной величина массового расхода топлива,
тогда как в настоящее время технически реализуемо только объемное
дозирование;
- параметры топлива: зольность, влажность, распределение частиц топлива по размерам предполагают заранее
известными и для получения динамических характеристик системы необходимо производить каждый раз новый цикл
вычислительных операций;
- не учитывается наличие термического разрушения и механического истирания частиц топлива в кипящем слое;
- сложность корректировки параметров модели при получении новых экспериментальных данных или ее использования
для различных марок топлива ограничивает область применения полученных зависимостей.
Таким образом, целью работы является синтез на основе существующих аналитических зависимостей математической
модели топки НТКС с решением следующих задач:
- учет особенностей технологического оборудования и условий окружающей среды;
- возможность изменения основных характеристик топлива непосредственно в процессе моделирования как в ручную,
так и по заранее заданному алгоритму.
В случае рассмотрения топки как объекта автоматизации в первую очередь вызывают интерес динамические свойства
системы, которые далее используются для управления. При традиционном подходе к рассмотрению данного вопроса
скорость отклика объекта на динамические возмущения оценивается с помощью уравнения теплового баланса [1]:
где сg, ссл – теплоемкость газа и материала слоя;
pg, pсл – плотность газа и насыпная плотность материала слоя;
Sсл – площадь зеркала горения;
Нсл – высота слоя ;
Тсл, T0 – температура слоя и газа;
QТ – теплота сгорания топлива;
jТ – расход топлива на 1 м2 площади зеркала горения, (кг/м2*с);
U0 – скорость газа через слой;
q3, q4 – доля химического и механического недожега;
Iз, Iл – потери теплоты с отводимой золой и излучением.
Однако такой подход имеет целый ряд недостатков:
- величины сg и ссл при изменениях Тсл в пределах существования слоя не являются константами, а следовательно
имеет смысл вместо теплоемкостей пользоваться удельными энтальпиями;
- расход теплоты при прогреве твердого топлива не учитывается;
- при определении теплоты, выносимой из слоя смесью газов, не учитывается химический состав поступающей в слой
и исходящей из слоя смеси;
- массовое дозирование топлива возможно только в лабораторных условиях, а в ре-альных условиях применимо лишь
объемное дозирование;
- при изменении расхода топлива не учитывается , что мгновенное значение теплоты, получаемое от сгорания,
существенно зависит от его гранулометрического состава.
Для разрабатываемой математической модели принимаются следующие допущения:
- масса инертного материала МСЛ, находящегося в слое, является постоянной величи-ной, с учетом непрерывно
работающей системы золоудаления;
- топливо, поступающее в слой, имеет полидисперсный состав, который подчиняется нормальному закону
распределения, переменной составляющей кторого является математическое ожидание эквивалентного диаметра
частиц dmo [5];
- исходящая из слоя смесь газов имеет температуру, равную Тсл [6];
- при работе котлоагрегата НТКС возможен переход с одной марки топлива на другую с изменением основных
параметров (зольности, влажности и т.д.).
Исходя из изложенного, уравнение теплового баланса имеет вид:
где Iсл – удельная энтельпия инертного материала слоя, ккал/кг.
В свою очередь, зависимости Iсл=f(Тсл) и Тсл=f(Iсл) при моделировании задаются массивом данных.
Рассмотрим последовательно все составляющие правой части выражения (2).
Количество теплоты в единицу времени – Qgt, получаемое от сгорания жидкого топлива при розжиге:
где Vgt - объемный расход жидкого топлива ;
pgt - плотность жидкого топлива;
Qgt- низшая теплота сгорания жидкого топлива, ккал/кг.
Количество теплоты в единицу времени - Qv , вносимое в топку дутьевым воздухом:
где Tv - температура дутьевого воздуха, гр. С;
Qdv- производительность дутьевого вентилятора;
Iv- удельная энтальпия воздуха, Iv=f(Тv) - массив данных.
Количество теплоты в единицу времени QT1 ,QT2 и QTn1 ,QTn2, вносимое в топку при сгорании сухой горючей массы
топлив 1 и 2, и забираемое при нагреве этих масс до температуры слоя соответственно.
Подробнее рассмотрим определение величин QT1 и QT2. Для величин QTn1, и QTn2 алгоритм определения будет
аналогичным. С целью упрощения выражений индексы топлив 1 и 2 опущены для всех переменных,
кроме dt1 и dt2 – объемных долей соответствующих топлив в производительности забрасывателя. Первоначально
определяется массовый расход сухой горючей составляющей топлива:
где pu - плотность сухой горючей массы;
pp- плотность породы;
Vz- объемная производительность забрасывателя;
Ap- зольность топлива.
При моделировании предполагается, что сухая горючая масса распределяется по ряду ячеек,
каждая из которых соответствует определенному диапазону диаметров частиц dmax,…dj,…dmin. Нумерация ячеек
производится начиная с минимального диаметра. Текущий массовый расход для каждой ячейки определяется, как:
где F(d,dmo)- функция распределения частиц по диаметрам в зависимости от текущего математического ожидания.
Полагается, что все частицы, попавшие в одну ячейку, имеют одинаковый расчетный диаметр:
Во время нахождения в j-ой ячейке частицы последовательно проходят следующие стадии: прогрев до температуры
слоя, выход и горение летучих, выгорание коксового остатка до , после чего происходит переход коксового остатка
в ячейку j-1 [1]. Отбор теплоты на прогрев горючей массы из одной ячейки и получение теплоты от горения летучих
и коксового остатка определяются из выражений:
где trj,tlj,tgj - время пребывания частиц в каждой из стадий, значения задаются в виде массива данных по
результатам экспериментальных исследований [1, 7] и могут быть в дальнейшем скорректированы без изменения структуры
модели;
Qn- низшая теплота сгорания в пересчете на сухую горючую массу;
Gtrj(t)- массовый расход частиц, подвергнувшихся терморазложению или измельчению [3].
Далее определяется QT, и так далее для QT1, QTn1 и QTn2.
QTnn1 и QTnn2- количество тепла в единицу времени, отбираемое из топки на прогрев породы, определяются
аналогично QTn1 и QTn2.
Qh2o- количество тепла в единицу времени, отбираемое из топки на испарение и прогрев до температуры слоя
содержащейся в топливе влаги. При этом предполагается, что данный процесс происходит мгновенно после попадания
топлива в слой.
Qd1, Qd2,Qdgt, Qvo- количество тепла в единицу времени, отбираемое из топки продуктами горения твердых и
жидкого топлив, а также не прореагировавшим остатком дутьевого воздуха. С учетом того, что массы выгорающих в
единицу времени топлив известны, определение значений не составляет сложности.Таким образом, имеется
возможность определения из выражения (2) текущей энтальпии слоя, а следовательно, и его температуры, т.е.
основного технологического параметра. Предложенная математическая модель реализована в прикладном пакете MATLAB.
На рис. 1а и 1в приведены полученные в разработанной математической модели реакции температуры слоя на
ступенчатое изменение производительности забрасывателя для dmo=3 мм и dmo=10 мм соответственно. Моделирование
производилось для следующих исходных данных: высота кипящего слоя Н=0,4 м, площадь S=2 м2,зольность топлива А=50%,
влажность W=8%, производительность вентилятора Qvd=2,5 м3/с, марка угля – жирный.
Рисунок 1 – Результаты моделирования
переходных процессов
Анализируя полученные зависимости, можно сделать вывод, что передаточная функция топки НТКС по контуру
"топливо" имеет вид:
причем длительность запаздывания прямопропорционально зависит от математического ожидания диаметров
частиц dmo, что хорошо видно на рис. 1б и 1г, на которых укрупнено показано начало переходных процессов.
Разработанная математическая модель позволяет получить переходные характеристики топки кипящего слоя при
переменных параметрах топлива и режимах работы, а также в дальнейшем осуществить синтез системы
автоматического управления топочными процессами.
Список использованной литературы
1. 1. Махорин К.Е., Хинкис П.А. Сжигание топлива в псевдоожиженном слое. – К.: Наукова думка, 1989. – 204 с.
2. Корчевой Ю.П., Пацков В.П., Редькин В.Б., Майстренко А.Ю. Расчет выгорания частиц твердого топлива в
кипящем слое с учетом внутрипористого реагирования// Тепломассообмен ММФ-92. Тепломассообмен в дисперсных
системах: Т.5.-Минск. АНК"ИТМО им. А.В. Пылова", АНБ. – 1992.– С. 168–170.
3. Бубенчиков A.M., Старченко А.В., Стропус В.В. Математическое моделирование аэродинамики и
тепломассопереноса в устройствах с циркулирующим кипящим слоем // Теплоэнергетика. – 1995. – № 9. – с. 37–41.
4. Рохман Б.Б., Шрайбер А.А., Чернявский Н.В. Инженерная методика расчета cгорания твердых топлив
в реакторе с циркулирующим кипящим слоем применительно к пилотной установке по технологии
фирмы "Лурги" // Пром. теплотехника. – 2004. – т. 26. – № 4. – с. 40-47.
5. Бородуля В.А., Гупало Ю.П. Математические модели химических реаторов с
кипящим слоем. – Мн.: Наука и техника, 1976, 208 с.
6. Забродский С. С. Гидродинамика и теплообмен в псевдоожиженном (кипящем)
слое. М.–Л., Госэнергоиздат, 1963. 488 с.
7. Бородуля В.А., Пальченок Г.И., Васильев Г.Г., Дрябин В.А.,
Галерштейн Д.М. Тепломассообмен и кинетика горения твердого топлива в
кипящем слое // Проблемы тепло- и массообмена в современной технологии
сжигания и газификации твердого топлива. Мате-риалы международной
школы-семинара. Минск, 1988, ч. 2. – с. 3–23