В.И. Ткачук, канд. техн.наук

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЕНТИЛЬНОГО РЕАКТИВНОГО
ДВИГАТЕЛЯ

       Вентильные двигатели, сочетающие в себе удобство регулирования коллекторных машин постоянного тока с технологичностью и надежностью индукционных машин находят все более широкое применение в ответственных регулируемых электроприводах.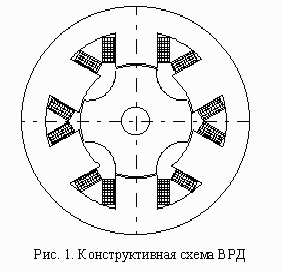 Одним из самых простых по конструкции и, в то же время, с высокими энергетическими показателями, является вентильный реактивный двигатель (ВРД) постоянного тока с явнополюсным статором и произвольным числом магнитоизолированных фаз (рис.1), электронным коммутатором (ЭК) с последовательным емкостным накопителем энергии (ЕНЭ) (рис.2) и с датчиком положения ротора (ДПР) произвольного типа.

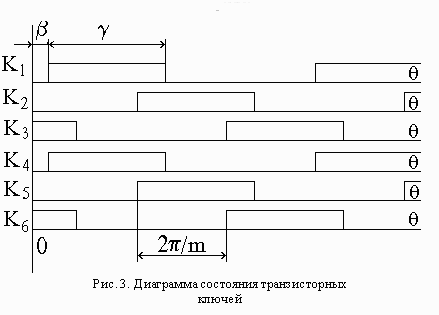
       Процесс работы ВРД можно предста-вить следующим образом. При угле положения ротора q, равном углу включения b (рис. 3), сигнал ДПР открывает транзисторные ключи VT1 и VT4 ЭК, которые будут открыты на протяжении угла коммутации g . Фаза W1 получает питание от источника и согласно с ним включенного конденсатора С1, заряженного в предыдущем цикле через эти ключи. Диод VD2 будет закрыт приложенным к нему в обратном направлении напряжением конденсатора С1.

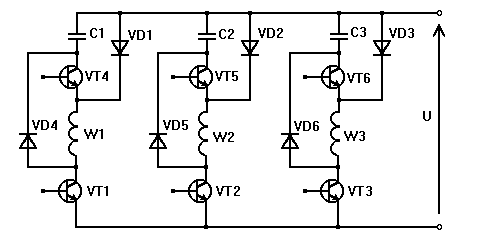
Рис. 2. Принципиальная схема ЭК с последовательными ЕНЭ в каждой фазе

Ток фазы форсированно возрастает, конденсатор С1 разряжается и когда напряжение на нем будет равно нулю, откроется диод VD1, а фаза W1 остается подключенной к источнику питания через диод VD14, транзисторный ключ VT1. Под действием электромагнитного момента ротор поворачивается и при достижении угла коммутации g закрываются ключи VT1 и VT4. Под действием ЭДС самоиндукции ток фазы W1 будет протекать по цепи: диод VD1, конденсатор С1, диод VD4. Конденсатор С1 заряжается, ток фазы W1 форсированно уменьшается. Для других фаз этот процесс повторяется через угол 2p/m, где m - число фаз.

      Задача исследования электромеханических процессов в переходных и квазиустановившихся режимах работы состоит в математическом описании ВРД системой дифференциальных уравнений электрического и механического равновесий с последующим их решением относительно токов фаз.

       В общем случае электромагнитный момент электромеханического устройства определяется производной магнитной коэнергии по углу перемещения, которая в свою очередь зависит от потокосцепления возбужденного контура. Отсюда, для расчета электромагнитного момента ВРД с магнитоизолированными фазами необходимо и достаточно наличие выражения зависимости потокосцепления фазы от тока и угла взаимного положения ротора и статора.

       Потокосцепление магнитоизолированной фазы ВРД является однозначной нелинейной функцией, которая может быть аппроксимирована аналитическим выражением. При этом необходимо, чтобы способ аппроксимации обеспечивал достаточно точное совпадение реальных и аппроксимированных зависимостей как в функции угла, так и в функции тока, возможность интегрирования и дифференцирования в аналитической форме, не требовал сложных и громоздких расчетов коэффициентов. В [1] предложено такое выражение для аппроксимации:

,

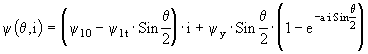(1)

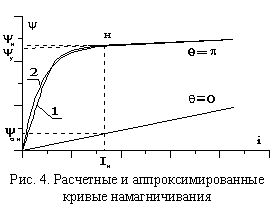
где q - электрический угол между осями паза ротора и зубца статора; i - ток возбужденной фазы; y₁₀, y_lt, y_y - коэффициенты, которые определяются из расчетных характеристик намагничивания магнитопровода ЭМП в двух крайних положениях: при совпадении осей паза ротора и зубца статора (q = 0) и при соосных зубцах ротора и статора (q = p) (рис. 4).

       Коэффициент y₁₀ = y_ii /I_i (см. рис. 4). Для определения остальных коэффициентов необходимо экстраполировать насыщенный участок кривой намагничивания (q = p) на ось ординат y . При этом получим точку "н" с координатами I_i,y_i и коэффициент y_y, откуда

y_lt = y₁₀ - (y _OH - y_y)/I_H    и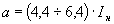   

       Приведенное на рис. 4 сравнение расчетной (1) и аппроксимированной (2) кривых намагничивания, вид аппроксимирующего выражения и способ определения коэффициентов свидетельствуют об удачном выборе аппроксимации.

      Согласно теории электромагнитного преобразования энергии из (1) получено выражение для мгновенного значения электромагнитного момента:

,

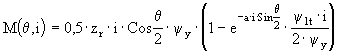(2)

где z_r - число зубцов ротора.

       Очень часто при математическом моделировании электромеханических процессов пренебрегают потерями в стали из-за их будто бы незначительного влияния. Однако в параметрических ЭМП частота коммутации достаточно высокая и потери в стали соизмеримы с другими видами потерь. Точный расчет потерь в стали с учетом явлений магнитного последействия, поверхностных и пограничных эффектов сложная и громоздкая задача. В ВРД основной магнитный поток не изменяет своего направления, а лишь амплитуду. Значит в общей доле потерь доминирующую роль играют потери от вихревых токов, и потерями от гистерезиса можно пренебречь. В этом случае сечение магнитопровода представим в виде элементарных замкнутых контуров, а их в схеме замещения фазы ВРД - в виде ветви L_s и R_s, которая подключена параллельно намагничивающему контуру. R_s для одной фазы рассчитываем по выражению:

,

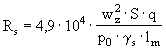(3)

где p₀, g_s, S, I_m, w_z, q - удельные потери в меди, плотность материала магнитопровода, площадь поперечного сечения магнитопровода, длина магнитной силовой линии, число витков обмотки на одном зубце, число зубцов статора на одну фазу соответственно.

       При моделировании силовых транзисторных ключей можно принять их безынерционными. Вольт-амперная характеристика (ВАХ) насыщенного ключа описывается выражением:

DU_T = U_КЭ.0 + R_КЭ.НАС ^.i ,

где U_КЭ.0 и R_КЭ.НАС - определяются из паспортных данных транзистора. Сопротивление закрытого ключа принято равным бесконечности.

       Состояние ключей ЭК опишем формальными коэффициентами K_j, которые принимают значение "1" - если ключ открыт, и "0" - если ключ закрыт; j - номер ключа. На рис. 3 приведен пример диаграммы работы ключей ЭК трехфазного ВРД с последовательными ЕНЭ в каждой фазе.

       Значения формальных коэффициентов определяются согласно переключающей функции:

,

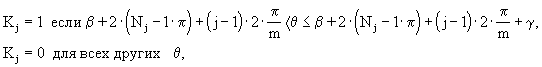(5)

где 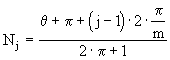- номер периода для соответствующей фазы.

       В схеме ЭК присутствует нелинейный элемент - диод, ВАХ которого в соответствии с [2] можно аппроксимировать функцией:

,

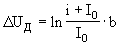(6)

где I₀, b - обратный ток диода и коэффициент температурного потенциала.

       В соответствии с алгоритмом работы ВРД, структура схемы включения фазы и уравнения дискретно изменяются при изменении угла q :

       - ключи VT1 и VT4 замкнуты, конденсатор С1 заряжен; происходит форсированное включение тока;
*     замкнут ключ VT1 и включен диод VD1, конденсатор разряжен
*  ключи VT1 и VT4 разомкнуты; происходит разряд энергии, запасенной в
   магнитном поле фазы и заряд конденсатора через диоды VD1 и VD4.

       С учетом вышесказанного, а также считая, что ВРД питается от источника с нулевым внутренним сопротивлением, для m-фазной машины с пассивным ротором, магнитоизолированными фазами и ЭК с последовательным ЕНЭ в каждой фазе составлены развернутые уравнения. Для их численного решения использован метод Рунге-Кутта с постоянным шагом интегрирования. Для точного определения моментов включения и выключения ключей ЭК, а также моментов, когда токи фаз и напряжения на конденсаторах достигают нулевых значений, применен метод инвертирования диференциальных уравнений [3].

       Компьютерная программа имеет высокий информативный уровень и позволяет исследовать электропривод с ВРД в динамике и статике, определять время разгона, пульсации электромагнитного момента и частоты вращения, в результате расчета получаем мгновенные значения токов фаз, электромагнитного момента и частоты вращения, средние значения потребляемого тока, потребляемой и полезной мощности, частоты вращения, потерь в коммутаторе, в меди, в стали в установившемся режиме, а также максимальные значения тока и напряжения на накопительном конденсаторе.

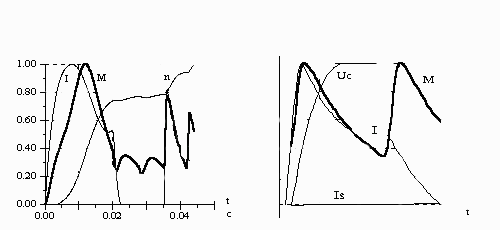
Рис. 5 Результаты расчета пускового и квазиустановшегося режимов работы трехфазного ВРД

       На рис. 5 приведен пример расчета пускового (ток одной фазы, электромагнитный момент и частота вращения в относительных единицах) и квазиустановившегося (ток фазы, момент, напряжение на накопительной емкости и ток,эквивалентирующий потери в стали) режимов работы электропривода на базе трехфазного ВРД с последовательными ЕНЭ в каждой фазе.

       При сравнении расчетных кривых токов фаз и напряжений на накопительных конденсаторах с экспериментальными осциллограммами расхождение по мгновенным значениям не превышает 10 %, что свидетельствует об достаточной степени адекватности математической модели физическому образцу.

       Разработанная математическая модель ВРД с ЕНЭ позволяет рассчитывать мгновенные значения тока в каждой фазе, электромагнитного момента, частоты вращения, а также анализировать влияние параметров двигателя на его рабочие характеристики.

       Используя предложенную модель, можно исследовать ВРД в статике и динамике, определять время его разгона, величину пульсаций электромагнитного момента и частоты вращения, оптимальные значения угла включения b и интервала коммутации g, максимальное значение тока в фазах и напряжения на накопительных конденсаторах, что необходимо для правильного выбора элементов полупроводникового коммутатора.

      Список использованной литературы.

      1. Ткачук В. Статичний момент електромеханічних перетворювачів з пасивним ротором. Електромеханіка. Теорія і практика. Праці науково-технічної конференції, присвяченої 100-річчю від дня народження видатного українського вченого-електромеханіка Т. Губенка. Львів. 1996. С. 177 - 180.

      2. Татур Т.А. Основы теорииэлектрических цепей. -М.: Выс. шк. 1980, -271 с.

      3. Фильц Р.В. Математические основы теории электромеханического преобразования энергии. -Киев: Наукова думка, 1979. -208 с.

Copyright © 1998-1999 Odessa State Polytechnic University. All Rights Reserved.