РАСЧЕТ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК ВЕНТИЛЬНОГО РЕАКТИВНОГО ДВИГАТЕЛЯ

УДК 621.435

В. И.Ткачук, канд. техн. наук

РАСЧЕТ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
ВЕНТИЛЬНОГО РЕАКТИВНОГО ДВИГАТЕЛЯ

Предложена математическая модель вентильного реактивного двигателя с емкостным накопителем энергии для средних значений, которая позволяет рассчитывать механическую, моментную и рабочие характеристики по известным геометрическим размерам и обмоточным данным.

Запропонована математична модель вентильного реактивного двигуна з ємнісним нагромаджувачем енергії для середніх значень, що дозволяє розраховувати механічну, моментну і робочі характеристики по відомим геометричним розмірам і обмоточним даним.

Switched reluctance motor (SRM) is the simpler, more technological and cheaper then other known electrical motors. In the paper the average values mathematical model for SRM is proposed, which give a way to calculate its static characteristics. Example of calculation of mechanical and working characteristics is presented.

Вентильный двигатель (ВД) - это электромеханическая система, состоящая из трех взаимосвязанных узлов: электромеханического преобразователя (ЭМП), датчика положения ротора (ДПР) и электронного коммутатора (ЭК). В качестве ЭМП чаще всего применяют индукционную машину с возбуждением от постоянных магнитов (ПМ), размещенных на роторе. Наличие ПМ на вращающейся части машины усложняет конструкцию и технологию изготовления, повышает стоимость. Одним из самых простых по конструкции, технологии и надежности является ЭМП с явнополюсным статором и сосредоточенными катушками обмотки якоря и зубчатым пассивным ротором. Такой ЭМП проще, дешевле и технологичнее самых простых из электричеcких машин - асинхронных с короткозамкнутым ротором, а ВД на их основе, называемые вентильными реактивными двигателями (ВРД), по регулиро-вочным свойствам не уступают коллекторным двигателям постоянного тока. Применение ЭК с емкостным накопителем энергии значительно улучшает энергетические показатели ВРД за счет более полной утилизации энергии магнитного поля. На рис. 1 приведена схема ЭК с отдельными последовательными накопителями в каждой фазе, а на рис. 2 - диаграмма работы его силовых транзисторных ключей, зависимости

©Ткачук В.И.,1998

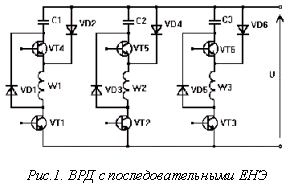
от угла взаимного положения ротора и статора индуктивности одной фазы, ее тока и напряжения на накопительном конденсаторе. Для исследования динамических и квазиустановившихся режимов работы электропривода на базе ВРД служит математическая модель ВРД для мгновенных значений [1]. Однако часто необходимы рабочие и механическия характеристики ВРД, для расчета. которых и предназначена предлагаемая упрощенная модель для средних значечений. Используя уравнение баланса средних на интервале переключения фаз значений мощностей

U ^. I_ = w ^. M + DP_M + DP_CT + DP_K , (1)

где U,I_ - средние значения напряжения и потребляемого от сети тока; w, M - средние значения частоты вращения и момента нагрузки на валу; DP_M, DP_CT, DP_K - мощности потерь в меди, в стали и в коммутаторе соответственно, можно получить выражение механической характеристики ВРД, 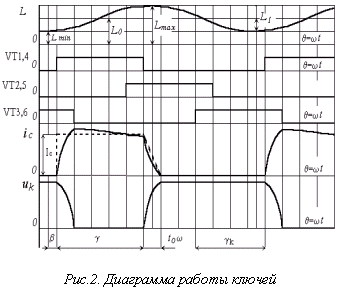а также виражения для составляющих потерь. Потребляемый ток, а значит, и среднее значение тока фазы при изменении частоты вращения в широком диапазоне и при постоянном моменте на валу не изменяются. Эта особенность позволяет определять электромагнитный момент ВРД в установившемся режиме по среднему на интервале переключения значению тока фазы.Учитывая особенности протекания электромагнитных процессов в ВРД, целесообразно принять некоторые допущения, которые позволят получить относительно простые выражения для среднего значения электромагнитного момента, а также отдельных составляющих потерь, практически не снижающие их точность: нелинейную магнитную цепь заменяем эквивалентной линейной, в которой насыщение стали учитывается коэффициентом насыщения 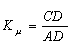(см. рис.3); - индуктивность фазы при взаимном перемещении ротора и статора изменяется по закону L = L₀ + L₁ ^. Cosq (см. рис. 2); - угол включения b (рис. 2) принимаем равным нулю; - полагаем, что силовые транзисторные ключи и диоды ЭК в закрытом состоянии имеют бесконечно большое сопротивление, а в открытом насыщенном состоянии мощность потерь учитывается прямым падением напряжения DU_k; динамическими потерями на переключение ключей пренебрегаем; - электромагнитным моментом, создаемым током фазы на интервале t₀ (с момента запирания силового транзисторного ключа) пренебрегаем, так как индуктивность фазы на указанном интервале изменяется незначительно; - на интервале возбуждения фазы g реальную кривую тока фазы заменяем средним значением I_¶, а на интервале спадания тока t₀ - по линейному закону, как показано на рис. 2; - механическими потерями пренебрегаем; - частоту вращения ротора на интервале переключения считаем неизменной.

Учитывая, что электромагнитный момент ВРД 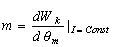[2], где 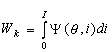- магнитная коэнергия, Q_m - геометрический угол между осями паза ротора и зубца статора, Q = Z_r ^. Q_m - этот же угол в электрических градусах, и изложенные допущения Z_r - число зубцов ротора; D,l - диаметр расточки и аксиальная длина статора; d - длина воздушного зазора между зубцами статора и ротора; w_z - число витков обмотки статора на одном зубце; a_s - коэффициент полюсного перекрытия статора; . (3)

Мощность потерь в меди расчитывается, как:

DP_M = I²_¶ ^. R_¶ ^. (g^* + k₁ ^. w) , (4)

где 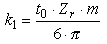- коэффициєнт, учитывающий потери в меди от тока заряда накопительного конденсатора, t₀ - время спадания тока фазы; 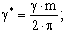; m - число фаз. Обозначим

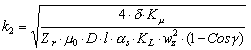(5)

Тогда 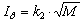и (4) запишем в виде: DP_M = k₂² ^. M ^. R_¶ ^. (g^* + k₁ ^. w). (6).

Учитывая, что в любой момент времени ток фазы протекает через два полупроводниковых элемента мощность потерь в ЭК расчитываем по формуле:

DP_K = I_¶ ^. 2 ^. DU_K ^. (g^* + k₃ ^. w) , (7)

где 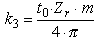(см. разъяснение коэфициєнта ).

Подставив (5) в (7), получим выражение для расчета потерь в коммутаторе в виде

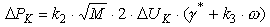(8)

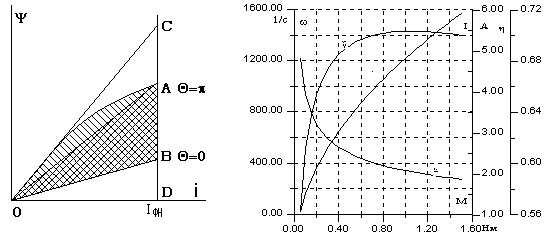
Рис.3. К определению коэффициента K_m

Рис. 4. Статические характеристики ВРД

В соответствии с принципом работы ВРД его фазы возбуждаются однополярным током и форма кривой магнитной индукции B(t) далека от синусоидальной. С другой стороны, в ВРД в любой момент времени перемагничивается только часть магнитопровода, причем потери от вихревых токов доминируют над потерями от гистерезиса. Поэтому потери в стали ВРД с большой достоверностью можно представить в виде:

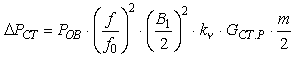(9)

где P_OB - удельные потери в стали от вихревых токов при индукции 1 Тл и частоте f₀ ; 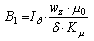- индукция в магнитопроводе при токе фазы I_¶ в момент, когда зубец ротора находится против зубца статора; k_v - коэфициент дополнительных потерь в стали от высших гармоник индукции; G_CT.P - расчетная масса стали, намагниченность которой изменяется при возбуждении одной фазы:

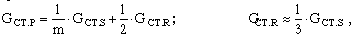
где G_CT.S, G_CT.R - масса стали статора и ротора соответственно.

Как (6) и (18) запишем формулу для расчета потерь в стали.

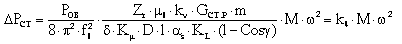(10)

где .

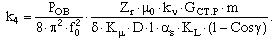Выразим ток фазы через ток от сети. В ВРД с последовательным ЕНЭ на интервале g от сети протекаєт ток только одной фазы, а на интервале перекрытия сигналов управления силовыми ключами - суммарный ток фаз, сигналы которых перекрываются. Поэтому

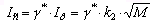(11)

Учитывая (5), (7), (10) и (11) и сгруппировав коэффициенты при степенях w, перепишем (1) в виде:

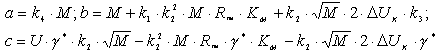(12)

Один из корней алгебраического уравнения (19), а именно - положительный является уравнением механической характеристики ВРД для средних значений.

Выражения (5), (7), (10) и (11) вместе с (4), (6) и (14) представляют математическую модель ВРД для средних значений, позволяют найти все основные величины, определяющие установившийся режим роботы двигателя для различных значений нагрузки на валу уже на стадии проектирования.

Для оценки адекватности математической модели физическому образцу на рис. 4 приведены расчетные характеристики для ВРД со следующими параметрами: D = 0.07 М, l = 0.03 M, d = 0.0003M, a_s = 0.45, Z_r = 10, m=3, K_L = 0.43, w_z = 85, g = 130 эл. градусов, t₀ = 0.001C, R_¶ = 1.3 Ом, DU = 1.5 В.

Проведенное сравнение с опытными данными свидетельствует о достаточной адекватности математической модели физическому образцу, что дает основание для рекомендации предложенной математической модели для расчета рабочих, регулировочной и механической характеристик вентильного реактивного двигателя с последовательным емкостным накопителем в установившихся режимах работы.

Список использованной литературы

1. Ткачук В.І., Осідач Ю.В. Математичне моделювання електромеханічних процесів в електроприводі з вентильним реактивним двигуном. Вісник Держ. ун-ту. "Львівська політехніка" Електроенергетичні та електромеханічні системи. - 1995. - № 288. -С. 83 - 90.

2. Ткачук В. Теорія створення електромагнітного моменту у вентильному реактивному двигуні. Електромеханіка. Теорія і практика. //Праці науково-технічної конференції, присвяченої 100-річчю від дня народження видатного українського вченого-електромеханіка Т. Губенка. - Львів, 1996. - C. 173 - 176.