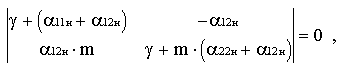|
УДК 621.313.333:681.3
ДИНАМИЧЕСКИЕ ТЕПЛОВЫЕ МОДЕЛИ УЗЛОВ ЭЛЕКТРИЧЕСКИХ МАШИН
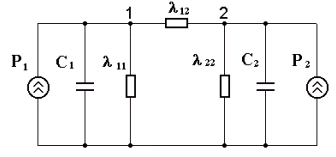
Модель представляет собой своеобразный многополюсник. На входы (вход) подаются сигналы, пропорциональные мощности источников тепла (потери в электрической машине), а на выходе получаем сигнал, пропорциональный температуре q(t) выбранного узла машины. Параметры схемы такого многополюсника определяются входными и выходными динамическими характеристиками. В этом случае входными характеристиками являются мощности источников тепла при различных коэффициентах нагрузки, а выходными — кривые нагрева (охлаждения) выбранного узла при различных условиях охлаждения, представляющие собой весовые характеристики или реакцию системы на скачок нагрузки. В качестве узла может быть выбран любой элемент конструкции электрической машины. Практическую ценность представляют элементы обмоток с наиболее напряженными тепловыми нагрузками. Например, для асинхронных двигателей (АД) с самовентиляцией такими являются лобовые части обмотки статора. С точки зрения условий охлаждения для АД следует выделить два режима: нагрев при вращающемся роторе и охлаждение (неподвижный ротор). Для многополюсников распространены Т и П-образные схемы замещения. На рис.1 приведена эквивалентная П-образная схема тепловой физической модели узла электрической машины.
Схема включает: два источника тепла P1 и P2, теплоемкости С1 и С2, тепловые проводимости l11, l12, l22. В узле 1 формируется температура выделенного узла электрической машины. Схема замещения имеет вид ЭТС с двумя узлами. В этом случае трактовка физических процессов может быть следующей. В узле 1 формируется температура выбранного узла электрической машины, а узел 2 отражает суммарную реакцию остальных элементов конструкции машины на тепловые процессы в рассматриваемом узле. Тогда величина Р1 соответствует потерям мощности в выбранном узле, а С1 — его теплоемкость. Если Р2 — потери мощности в остальной части машины, то величину теплоемкости С2 необходимо подбирать таким образом, чтобы тепловая энергия, запасенная в С2 в установившемся режиме, равнялась запасенной тепловой энергии в остальных элементах конструкции электрической машины. Подобный подход позволяет учесть суммарный тепловой баланс модели и реальной машины в целом. Параметры схемы должны быть подобраны таким образом, чтобы в схеме имели место адекватные тепловые переходные процессы в узле 1 модели и выбранном элементе электрической машины (например, лобовая часть обмотки статора АД). Уравнения, описывающие переходные процессы в предложенной схеме, имеют вид:
Решения системы уравнений 1 и 2 для режимов нагрева и охлаждения имеют вид:
Т1н и Т1ох — большие постоянные времени экспонент в режимах нагрева и охлаждения; Т2н и Т2ох — малые постоянные времени экспонент; А1н, А2н, А1ох, А2ох — коэффициенты удельного веса экспонент; qуст — установившееся превышение температуры узла АД при коэффициенте нагрузки Кнг. Выражения (3) и (4) отражают особенности форм кривых тепловых переходных процессов, получаемых при решении ЭТС с большим количеством узлов. Экспоненты с большой постоянной времени характеризуют общую длительность переходного процесса tпп, а экспоненты с малой постоянной времени отражают скорость изменения температуры dq / dt на начальных этапах тепловых переходных процессов. При t = 0 скорость изменения температуры в режиме нагрева и охлаждения соответственно
Расчет пассивных параметров ДТМУ основывался на следующем. При нулевых начальных условиях q1(0) = 0 и q2(0) = 0 имеем:
. Принимая во внимание (5), получим:
Определим остальные пассивные параметры схемы l11, l12, l22 и С2. Для этого запишем уравнения (1) и (2) в другом виде:
В установившемся режиме имеем:
тогда из уравнений (8) и (9) получаем:
Здесь q = qуст2 / qуст1 — относительный коэффициент изменения температуры в установившемся режиме. Ориентировочно можно принять q = 1. Характеристическое уравнение системы уравнений (8), (9)
Для обеспечения адекватности воспроизведения переходных процессов необходимо, чтобы корни характеристического уравнения
Тогда согласно теореме Виета
Рассматривая совместно уравнения (11), (12), (16) и (17), получаем единую систему четырех уравнений с четырьмя неизвестными, решение которой позволяет определить пассивные параметры схемы динамической тепловой модели при нагреве. |
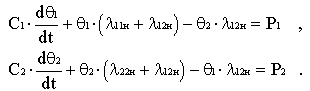
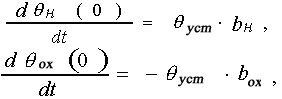
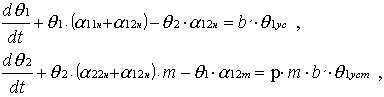
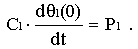
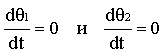 ,
а q1
= q1уст;
q2
= q2уст,
,
а q1
= q1уст;
q2
= q2уст,