В соответствии с общепринятой классификацией колебательных систем и процессов очистной или проходческий комбайн при выполнении рабочего процесса представляет собой автономную систему с конечным числом степеней свободы, определяющих динамическое состояние системы комбайн-забой в любой фиксированный момент времени. Особенность таких систем – возможность самовозбуждения и поддержания в них колебаний за счет внутреннего источника энергии неколебательной природы, например двигателя, причем поступление энергии регулируется движением самого комбайна, осуществляющего рабочий процесс отделения и выгрузки полезного ископаемого. Параметры установившихся автоколебаний в значительной степени определяются нелинейными свойствами системы. Наиболее существенные из них в системе комбайн-забой – это нелинейная кинетическая характеристика трения опор комбайна по направляющим конвейера и нелинейность резко переменных сил сопротивления, формирующихся на рабочих инструментах исполнительных органов, взаимодействующих с горным массивом со случайными характеристиками разрушаемости. Нелинейная зависимость силы трения в опорах комбайна от скорости обусловливает, как правило, возникновение автоколебаний в системе его подачи. Поэтому комбайн перемещается неравномерно, что является одной из причин периодического изменения суммарной толщины среза резцами исполнительного органа. Непостоянство сил сопротивления на исполнительном и тяговом органах, а также наличие упругих связей в составе силовых систем комбайна служат причинами формирования в системе сложных динамических процессов. Колебания силовых систем комбайна и обусловленные ими динамические нагрузки, в свою очередь, зависят от сил сопротивления на исполнительных органах, динамических параметров силовых систем и их взаимодействия между собой и с внешней средой – органа с разрушаемым горным массивом, а двигателя – с сетью электроснабжения. Анализ результатов исследований, сил сопротивления на исполнительных органах горных комбайнов показывает, что кроме низкочастотных (1-3 Гц) составляющих, обусловленных автоколебательным характером перемещения комбайнов, содержатся компоненты, отражающие силовую неуравновешенность исполнительного органа (степень его конструктивного несовершенства), проявляющуюся с частотой его вращения. Вместе с тем, существуют колебательные составляющие, частота которых практически совпадает с частотой собственных колебаний механической части системы привода исполнительного органа. Кроме автоколебаний и детерминированных колебаний, которые можно рассматривать как вынужденные, в силовых системах комбайнов возможны колебания, возбуждаемые внутренними источниками энергии, а также параметрические колебания вследствие периодических изменений тех или иных параметров динамических систем. К их числу можно отнести периодические изменения жесткости зубчатых передач при смене однопарного зацепления двухпарным, периодические удары в зацеплениях из-за неточностей их изготовления и монтажа и др. Таким образом, в общем случае динамические процессы и сопутствующие им динамические нагрузки в силовых системах комбайнов являются результатом взаимодействия рабочего процесса в системе комбайн-забой с колебаниями в самом комбайне и в значительной степени определяются его динамическими свойствами. Зная закономерности формирования динамических нагрузок и управления динамическими свойствами комбайна, можно на стадии проектирования обосновать его рациональные динамические параметры и структуру, обеспечивающие минимальную динамическую нагруженность наиболее ответственных и тяжело нагруженных элементов силовых систем. Повышение надежности горных комбайнов может быть обеспечено оптимизацией их динамических свойств и снижением динамических нагрузок, так как повышенная динамическая нагруженность, характерная для эксплуатирующихся в тяжелых условиях высокоэнерговооруженных комбайнов, является одной из основных причин недостаточной их надежности. Высокие коэффициенты вариации (0,3-0,65) крутящего момента и циклические свойства динамических нагрузок обусловливают ускорение накопления усталостных повреждений, интенсификацию износа и повышение вероятности отказов. Особенно заметно возрастают число и частота отказов элементов силовых систем очистных комбайнов, осуществляющих выемку пластов угля с крепкими включениями, породными прослойками, с присечкой боковых пород. Это обусловлено ростом амплитуд колебаний и максимальных значений экстренных нагрузок, которые могут превысить уровень несущей способности отдельных элементов комбайнов. Автоколебательные явления на собственных частотах силовых систем и сопутствующие им динамические нагрузки формируются также в системе подвески исполнительного органа и в системе корпусной группы очистных комбайнов. Динамические нагрузки, формирующиеся в СПРО, снижают надежность гидродомкрата подъема исполнительного органа, узлов шарнирного соединения корпусов поворотного и основного редукторов между собой и с гидродомкратом. Динамическая нагруженность СКГ отрицательно сказывается на надежности фланцевых соединений сборочных единиц, гидродомкратов регулируемых опор и других элементов опорно-направляющих устройств очистных комбайнов. Автоколебания в системе подачи очистного комбайна и присущая автономным системам замкнутость через забой обусловливают пульсацию нагрузок с частотой колебаний скорости перемещения комбайна не только в СМП, но и в других силовых системах. Циклические нагрузки тягового органа, редуктора механизма подачи и гидросистемы насос-гидромотор снижают усталостную прочность указанных элементов. При лимитированных габаритах очистных комбайнов возможности повышения несущей способности и усталостной прочности тяжело нагруженных элементов силовых систем за счет увеличения размеров деталей и применения более прочных материалов в значительной степени ограничены. Для изучения колебательных процессов, формирующих динамические нагрузки и управления динамическими свойствами комбайна, применяют математическое моделирование. Целью создания математической модели является установление связи между уровнем динамической нагруженности силовых систем, их структурой и параметрами с учетом спектрального состава внешней нагрузки и взаимодействия силовых систем, что дает возможность решить задачу комплексной оптимизации динамических свойств комбайнов. Математическое моделирование с помощью математических пакетов сводится к численному решению системы дифференциальных уравнений, которые описывают объект исследования, в результате чего получают кинематические и силовые характеристики механизма перемещения в переходных и установившихся режимах. Для наглядности результатов моделирования, рассмотрим случай возникновения автоколебаний при движению комбайна на холостом ходу. Для этого рассмотрим простейший случай, систему с одной степенью свободы. Дифференциальное уравнение имеет вид:

 

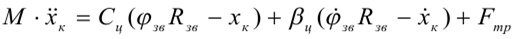
Исследование динамических процессов, применительно к очистным комбайнам с цепным тяговым органом автономную систему комбайн-забой можно заменить незамкнутой динамической системой. При разработке расчетной схемы вынесенной системы перемещения были приняты следующие допущения: тяговый орган представлен как линейный упруго-диссипативный элемент (с коэффициентами жесткости и демпфирования соответственно Cц, βц, работающей только на растяжение, масса цепи приведена к массе комбайна; корпуса редукторов ВСП и оси тяговых звездочек закреплены абсолютно жестко. Расчетная схема вынесенной системы перемещения для общего случая приведена на рис.1.

Рисунок 1 – Динамическая схема ВСП для общего случая

На схеме приняты следующие обозначения: Мд – электромагнитны момент электродвигателя; Jд – момент инерции ротора электродвигателя; Jзв – момент инерции приводной звездочки; Ст – коэффициент жесткости редуктора привода ВСП; βm – коэффициент демпфирования редуктора привода ВСП; Сц – коэффициент жесткости цепного тягового органа; βц – коэффициент демпфирования цепного тягового органа; G – сила тяжести комбайна; Fсопр – сила сопротивления движению массы M; Fтр – сила трения; В качестве обобщенных координат для математического описания системы приняты: φдв – угол поворота ротора двигателя; φзв – угол поворота приводной звездочки; xк – перемещение массы М (перемещение комбайна). 

Для составления системы дифференциальных уравнений, описывающих движение механической системы ВСП, используем уравнения Лагранжа II рода. Система дифференциальных уравнений, описывающая динамические процессы в ВСП, полученная на основе уравнений Лагранжа II рода, имеет вид:

где Rзв – средний радиус приводной звездочки; Решить такую систему дифференциальных уравнений можно методом Рунге-Кутта. 

Для решения системы будет нужен только вектор правых частей системы уравнений.

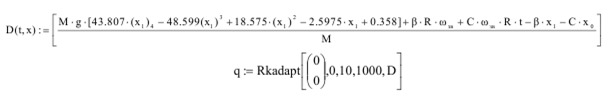
где х0 и х1 – известные функции перемещение и скорость комбайна соответственно. 

Показанная математическая модель процесса функционирования очистного комбайна с вынесенной системой подачи учитывает все основные факторы, определяющие интенсивные рабочие режимы комбайна. Анализ научно-технической литературы по вопросу исследования механизмов перемещения очистных комбайнов показал, что существующие математические модели не в полной мере пригодны для корректного описания динамических процессов в элементах вынесенных систем перемещения с частотно-регулируемым приводом при их работе в длинных очистных забоях. 

В связи с этим актуальной является задача разработки корректных математических моделей рабочих процессов очистного комбайна с вынесенной системой перемещения на основе частотно-регулируемого привода и использование этих моделей, а также разработанных критериев для обоснования структуры и параметров системы перемещения нового технического уровня.

Список использованной литературы

1. Введение в математическое моделирование. Учебное пособие. Под ред. П.В. Трусова. – М.: Логос, 2004. – ISBN 5-94010-272-7
2. Малков С.Ю., 2004. – Математическое моделирование в динамике: подходы и модели // Ред. М.Г. Дмитриев. – М.: РГСУ. – с. 76–188.
3. Самарский А.А., Михайлов А.П. – Математическое моделирование. Идеи. Методы. Примеры.. – 2-е изд., испр. – М.: Физматлит, 2001. – ISBN 5-9221-0120-X
4. Советов Б.Я., Яковлев С.А. – Моделирование систем: Учеб. для вузов – 3-е изд., перераб. и доп. – М.: Высш. шк., 2001. – 343 с. – ISBN 5-06-003860-2