Менгран Чжоу, Женби Ли - Исследования на угольных шахтах системы газового мониторинга контролируемого с помощью алгоритма имитации отжига

Аннотация

Менгран Чжоу, Женби Ли. Исследования на угольных шахтах системы газового мониторинга контролируемого с помощью алгоритма имитации отжига. Эта статья устанавливает принцип и схему газотранспортной системы мониторинга с помощью инфракрасного метода. Алгоритм имитации отжига принят для нахождения всех оптимальных решений, критерий Метрополиса используется для создания итерационного алгоритма оптимизации сочетаний с помощью контроля параметров снижения нацеленности на решение крупномасштабных проблем оптимизации сочетаний. Результат эксперимента, полученный с помощью выполнения схемы реализации алгоритмов обучения и поток реализации алгоритма обучения указывают, что алгоритм имитации отжига, принятый для идентификации газа, лучше чем традиционный линейный метод локального поиска. Алгоритм быстро выполняет итерации к оптимальному значению, следовательно, эффективно улучшается качество решения. Использование процессорного времени сокращается, а скорость определения газа увеличивается. Для шахт с большой газоносностью пластов может быть реализован опережающий прогноз. Увеличивается надежность безопасности на угольных шахтах.

Текст статьи

1. Введение

В Китае опасность выброса газа всегда являлась большим врагом безопасности на угольных шахтах и в настоящее время стала основным фактором, ограничивающим производство на шахтах. В настоящее время на угольных шахтах часто происходят аварии, особенно взрывы опасного газа, приводящие к серьезным экономическим потерям, которые уже привлекли большое внимание руководителей на всех уровнях. Вместе с улучшением процесса добычи и техники и расширением масштабов добычи и глубины, увеличивается количество выделяющегося каменноугольного газа, и скрытая проблема принимает все большие масштабы. Доля несчастных случаев, произошедших из-за взрывов газа на угольных шахтах, все время увеличивается. Поэтому, если несчастные случаи, произошедшие по вине газа, не удастся контролировать, стабильное улучшение безопасности ведения работ на угольных шахтах провалится, и непрерывное безопасное развитие угольных шахт отрасли не будет гарантировано.

Газоанализатор является важным аспектом контроля и управления производственной безопасностью на угольной шахте. Построение системной, всесторонней системы газового мониторинга шахты в режиме реального времени может помочь контролировать безопасность шахты, производство шаг за шагом, а также контролировать, предотвратить и уменьшить несчастные случаи. Разработка метода газового мониторинга в режиме реального времени, а также оборудования и газового контрольного датчика плотности с функцией саморегулирования – важная линия защиты и гарантии предотвращения несчастных случаев, произошедших по вине газа. Когда количество газа в рабочей области достигает критического значения, система газового мониторинга дает своевременный аварийный сигнал, проводятся измерения, и авария пресекается в корне.

С помощью исследования в области методов предотвращения и мониторинга взрывов газа на угольных шахтах, разрабатываемая система прогноза аварий может реализовать региональный прогноз и аварийный расширенный прогноз на шахтах опасных по газовому фактору.

Путь, используемый лазерным спектром поглощения для измерения поглощения газовой молекулы, принимается с высоким показателем качества. При изучении спектральных линий поглощения молекул газа с помощью лазера, ширина линии лазера может достигать 10^-4см^-1, это намного меньше, чем ширина линии поглощения газовой молекулы. Могут быть получены очень хорошая избирательность и разрешение, потому что лазер имеет очень узкую ширину линии. Текущая модуляция лазера проста в применении для всех видов режима модуляции и может увеличить чувствительность измерения, значительно стремясь к изолированному исследованию линии поглощения молекулы газа.

Этот пункт будет играть ведущую роль в выполнении количественного мониторинга газа в режиме реального времени на угольной шахте с помощью газоанализатора с лазерным спектром поглощения. В настоящее время способом контроля концентрации метана, главным образом, является газовая хроматография, этот способ не может осуществлять непрерывный контроль, потому что дает данные не менее чем через несколько минут. Использование спектра лазерной частоты сигнала дает возможность контролировать химический состав газа по-новому. Этот элемент пригоден для системы газового мониторинга с поисками онлайнового, быстрого оптического дистанционного зондирования в реальном времени и автоматического контроля оборудования. Такая система позволит сократить отставание страны от развитых стран и дает предпосылки стране для оптико-механическо-электрической интеграции в новую индустрию мониторинга точного состояния объекта исследования.

2. Газовые инфракрасные системы мониторинга

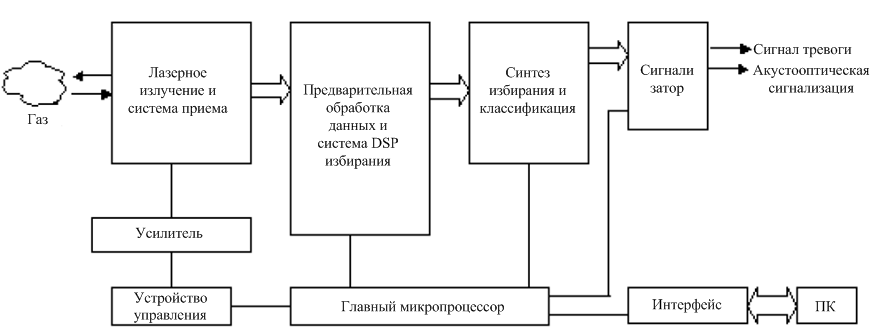
Рисунок 1 – Структурная схема газовых инфракрасных систем мониторинга

Газовая система аварийной сигнализации дистанционного мониторинга состоит из информационной подсистемы получения спектра и информационной подсистемы избирания спектра. Первая содержит оптический телескоп и консервирующий контроллер. Приемник интерферометра это датчик, установленный в радиометре спектра, который используется для получения инфракрасной информации о спектре. Информационная подсистема избирания спектра, также названная различителем, является интеллектуальной частью в природе. Его функция различения газа осуществляется с помощью микропроцессора за счет выполнения программы избирания. Кроме того, компьютер выполняет функцию визуального отображения сигнализации и общего контроля.

Плата DSP, сканируя электрическую машину и радиометрический спектр инициализируется впервые, когда система начинает выполнять операцию. Затем проба газового спектра в каждой позиции поочередно передается и сохраняется в соответствующей ячейке внутренней памяти. Со второго опроса, если предел концентрации газа на объекте не появлялся раньше, система не дает сигнал тревоги, изменения в фоновом режиме используются как новые данные спектра образца исходных данных, а не начальные. Если предел концентрации газа на объекте появляется в будущем, то система меняет его в спектре сигнала, вычитает его из фона спектра, делает предварительную обработку и дает в конце аварийный сигнал. Система циркулирует и работает непрерывно.

3. Принцип алгоритма имитации отжига

Алгоритм имитации отжига является эффективным приближенным алгоритмом для общего использования, пригодным для решения крупномасштабных задач оптимизации комбинаций. А также этот алгоритм является эффективным способом поиска всех оптимальных решений и имитирует процесс отжига плавления металла.

Каждый участок комбинаций оптимального решения в пространстве представляет одно решение. И другое решение имеет другую цену (так называемую функцию объекта). Оптимизация заключается в нахождении минимума (или максимума) решения к цене функции в области решений.

Представленное ниже математическое выражение может быть использовано, чтобы выразить этот алгоритм и решить проблему оптимизации комбинаций.

где f(x) является функцией объекта, g(x) – ограничительное уравнение, D – область определения.

Предположим, что проблема, которая будет решена, состоит в том, чтобы найти минимум многовариантной весовой функции. И можно использовать простой итеративный алгоритма локального поиска для нахождения минимального веса. В алгоритме локального поиска, начиная с некоторого заданного начального решения, новые решения производится в случайном порядке. Если вес нового решения меньше, чем вес настоящего решения, то оно заменяет настоящее решение, в противном случае от этого нового решения отказываются. Алгоритм локального поиска производит новые решения непрерывно и в случайном порядке и повторяет описанные выше действия до нахождения решения с наименьшим весом. Но этот локальный поиск изменения решения каждый раз может попасть в локальный минимум и не сможет выбраться. Для того чтобы избежать поискового процесса, блокируемого в локальном минимуме, алгоритм имитации отжига может разрешить «поднимающееся перемещение», а именно, ухудшение решения с определенной вероятностью. Преимущество этого способа состоит в том, что алгоритм может сходиться к целому оптимальному решению при некотором определенном условии. На рисунке 2 представлено сравнение двух алгоритмов.

Рисунок 2 – Сравнение двух алгоритмов

3.1 Критерий Метрополиса

Критерий Метрополиса, выдвинутый Н. Метрополисом в 1953 году, является основой всего алгоритма имитации отжига. Во-первых, основное состояние системы определяется как текущее состояние и его энергия это E_i. Затем управляющий механизм выполняет перемещение некоторой частицы, выбранной наугад с маленьким приростом, и в результате получаем новое состояние j с его энергией E_j. Если E_j<E_i, новое состояние принимается как важное состояние. Если E_j>E_i, принято ли это новое состояние как важное состояние, зависит от вероятности, что система в состоянии, а именно

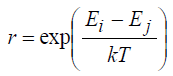
где r – число, меньше чем единица, ξ является случайным числом между нулем и единицой, произведенным генератором случайных чисел.

Если r<ξ, новое состояние j принимается как важное состояние, в противном случае от него отказываются.

Если новое состояние является важным состоянием, состояние j заменяет состояние i в качестве текущего состояния, иначе состояние i остается текущим состоянием. Процесс, производящий новое состояние, зацикливается.

Полученное по формуле (2), при высокой температуре, новое состояние с широким энергетическим разрывом между ним и текущим состоянием, может быть принято в качестве важного состояния. А при низких температурах, новое состояние с маленьким энергетическим разрывом между ним и текущим состоянием, может быть принято как важное состояние.

Это не противоречит эффекту теплового перемещения при различных температурах.

Когда температура стремится к нулю, любое новое состояние j, E_j>E_i, не может быть принято.

Вышеупомянутый критерий принятия нового состояния, называют алгоритмом критерия Метрополиса. При этом вычисление алгоритма значительно уменьшается.

3.2 Технологический процесс алгоритма имитации отжига

Введение критерия Метрополиса в процесс оптимизации и повторение критерия Метрополиса становится алгоритмом оптимизации комбинаций. Этот алгоритм, имитирующий твердый процесс отжига, называют, алгоритмом имитации отжига. Предположим, что решение проблемы оптимизации комбинаций i и ее функция объекта f(i) эквивалентны микрокосмическому состоянию i и ее энергии E_i соответственно. Предположим, что убывание алгоритма и параметр управления, играют роль температуры T в твердом процессе отжига, тогда итеративный процесс создания нового решения-суждения-принятия/отказа постоянно соответствует с процессом тела, склоняющегося к тепловому равновесию под некоторой постоянной температурой для каждого параметра управления t, что означает применение критерия Метрополиса. Алгоритм имитации отжига похож на критерий Метрополиса, в котором система конечного состояния получается из некоторых первичных состояний в процессе временной эволюции вычислительной системы. Относительное оптимальное решение проблемы оптимизации комбинаций данного параметра управления получается в результате множественной вариации некоторого основного решения. Когда температура плавно уменьшается в процессе твердого отжига, тело может достигнуть тепловое равновесие и склониться к стандартному состоянию с наименьшим количеством энергии. Таким образом, при плавном убывании параметра управления, полный оптимальный набор решения к проблеме оптимизации комбинаций может быть получен при помощи алгоритма имитации отжига.

Массивы решения оптимизации комбинаций получены с помощью алгоритма Метрополиса в алгоритме имитации отжига. Принят ли перенос от текущего решения i до нового решения j, зависит от переноса вероятности (P), соответствующей с критерием Метрополиса.

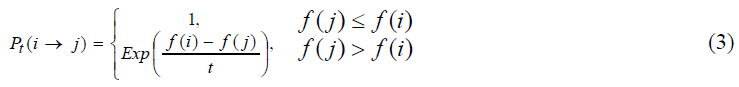
Из формулы (3) t ∈ R представляет собой параметр управления. Во-первых t является довольно большим (соответствует температуре плавления тела), и t плавно убывает после большого переноса (соответствует плавно убывающей температуре). Этот алгоритм повторяется и не останавливается, пока не встречает критерия остановки. Таким образом, имитационный отжиг может быть расценен как итерация алгоритма Метрополиса при прогрессивном убывании параметра управления. На рисунке 3 представлена блок-схема алгоритма имитации отжига.

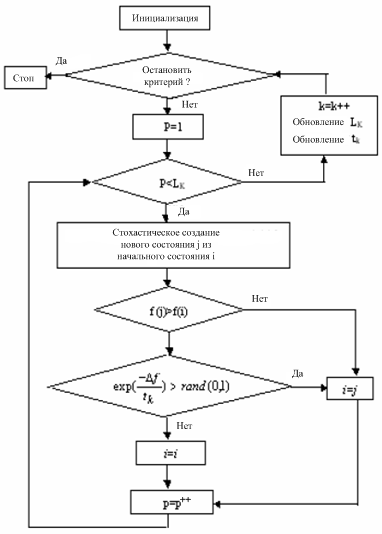
Рисунок 3 – Блок-схема алгоритма имитации отжига

4. Использование алгоритма имитации отжига для выбора алгоритма обучения

4.1 Схема реализации алгоритма обучения

В газовой системе мониторинга, для некоторой данной оценочной функции, используя учебный образец, устанавливают X, чтобы найти оптимальное решение, которое состоит в том, чтобы найти вектор решения W^*X>0, на основе которого 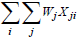выбирается как функция объекта (где j представляет график данных и i выражает номер выборки). Функция объекта также отвечает требованию того, чтобы быть суммой выражений нескольких оптимальных объектов функционирования и удовлетворяет запросу объектной функциональной оптимизации отражения выбора целой проблемы.

W^*X_ni(n = 1, 2 …) является измеренным значением расстояния между номером пробы i и поверхностью обнаружения. Итак, наибольшее значение W^*X_ni является наибольшим расстоянием между поверхностью обнаружения и центром двух проб и лучшим классификационным эффектом. Таким образом, эта система используется для нахождения максимума.

Набор решений содержит и выполнимое решение и неосуществимое решение. Генерация новых решений относится к градиенту происхождения. Для каждого веса W^*, поочередно проверяются выборки, затем выборки складываются и умножаются на размер шага, и прибавляются к прежнему весу W^* и получается новое решение.

Критерий Метрополиса принят как критерий допустимости

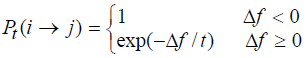
где t – параметр управления, Δf – функция объекта различия между существующим решением и новым решением.

Для остановки алгоритма используются три способа. Параметр управления убывает до того, как станет меньше, чем некоторое заданное число. Любое решение в непрерывной цепочке Мапкоба не может быть принято. Разница между генерацией старого решения W₀ и выборкой X и генерацией нового решения W₁ и выборкой X является меньше, чем некоторое число.

4.2 Поток реализации алгоритма обучения

Рисунок 4 – Использование алгоритма имитации отжига для алгоритма обучения

Предположим, что t_k это значение параметра управления, а L_k это длина линии Мапкоба, когда этот алгоритм выполняет итерации в k время. Случайное значение (0,1), полученное при помощи генератора случайных чисел, равномерно распределено между нулем и единицей. На рисунке 4 приведена подробная реализация потоков.

5. Заключение

Одна дегрессивная конечная последовательность {tk} параметра управления t и конечная последовательность Мапкоба k = 0, 1, 2, …, чья длина это L_k, приняты для управления алгоритмом имитации отжига вязкости с применением метода конечных промежутков времени. Таким образом, некоторые корреляционные параметры используются для обеспечения вязкости. Такими параметрами являются:

начальное значение параметра управления t: t₀;

функция затухания параметра управления t: α;

конечное значение параметра управления t (критерий остановки): t_f;

длина цепочки Мапкоба: L_k.

В эксперименте, предположим, что начальное значение параметра управления t: t₀ = 10, длина цепочки Мапкоба: L_k = 200 и конечное значение параметра управления t: t_f = 2 и получен эффект влияния α на конечное решение и время использования процессора, и эффект влияния выбора L_k на конечное решение и время использования процессора. В таблице 1 и таблице 2 представлены данные эффекта влияния.

Таблица 1 – Эффект влияния α на конечное решение и время использования процессора
α	Неправильно выделенные группы	Уровень избирания, %	Время использования процессора, с
0,70	3, 9, 16, 17, 23, 26, 29	85,4	5
0,80	13, 16, 22, 30, 32, 34, 36	85,4	8
0,85	16, 32, 34	93,8	10
0,95	16, 34	93,8	32

Таблица 2 – Эффект влияния выбора L_k на конечное решение и время использования процессора
L_k	Неправильно выделенные группы	Уровень избирания, %	Время использования процессора, с
200	2, 11, 13, 15, 22, 23, 28, 29, 30, 32, 34, 36, 38, 44, 52	68,8	3
400	13, 15, 22, 28, 30, 32, 34, 36	83,3	6
800	13, 16, 22, 30, 32, 34, 36	85,4	8
1000	16, 32, 34	93,8	11
1200	16, 34	95,8	12
2000	16, 34	95,8	23

Результат эксперимента и анализ теории соединяются в основных наблюдаемых данных в таблицах. Логические параметры могут обеспечить алгоритм вязкости. Если параметр плох, то процессор использует мало времени, но при этом наблюдается плохое качество конечного решения. Если параметр является хорошим, качество конечного решения улучшается, но время использования процессора увеличивается. Но параметры могут быть скорректированы и искусственно чередованы, чтобы улучшить качество окончательного решения для большей эффективности.

Библиографический указатель

1. Zhou Mengran, Li Zhenbi. Research on Coal mine Gas Detection with WMS Technique[C]. Progress in mining science and safety technology. Science Press USA Inc. 2007, 4: 933–937.
2. Zhou Mengran, Li Zhenbi et al. Data processing of coalmine gas spectrum single detect [J]. Coal Science Technology, 2006, 9: 45~49.
3. Zhou Mengran et al. Study on laser absorption spectroscopy for measuring gas of mine [J]. Applied Laser, 2004, vol.3.
4. Zhang Yin,Zhou Mengran. Application of artificial neural network BP Algorithm in near Infrared Spestroscopy. Infrared, 2006,11:1～4.
5. Kang Lishan, Xie Yun, etc. Non-numerical value collateral algorithm (The first volume) – Simulated annealing algorithm. The first page. Science Press, 2000,1~168.
6. Bian Zhaoqi, etc. Model Recognition. The first page. Qinghua University Press, 1988, 89~92 and 118~122.
7. Fang Yonghua, Xun Yulong. Infrared spectrum signal pretreatment. Infrared and laser engineering, 1998, 27(2): 17~22.
8. Flanigan D.F, Detection of Organic with Active and Passive Sensor: A Comparison.Appl.Opt., 1986,25(23): 4253~4254.
9. Lynn D.Hoffland, Ronald J.Piffath, James B.Bouck. Spectral Signatures of Chemical Agents and Simulates, Opt.Eng., 1985,24(6): 982~984.
10. D.F.Flanigan, H.P.D.Long, Spectral Absorption Characteristics of the Major Component of Dust Clouds, Appl.Opt., 1971,10(1): 51~56.
11. V.Janmes Cannuliato. James W.Kauffman, Pattern Recognition and Classification Techniques For The Army’s XM21 Remote Sensing Passive Chemical Agent Alarm, A.DEEPAK Publishing, 1985.