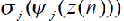- затраты исполнителя на выполнение j-ой работы в n-ом периоде,
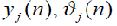– плановый и фактический объем j-ой работы выполненной исполнителем в n-ом периоде.Авторы: Богатырев В.Д., Гришанов Д.Г., Павлов О.В.
Источник: Управление большими системами / Сборник трудов молодых ученых. Выпуск 4. Общая редакция – Д.А. Новиков. М.:ИПУ РАН, 2003. – С.35-39.
Богатырев В.Д., Гришанов Д.Г., Павлов О.В. Механизмы согласованного управления инвестиционными проектами. В работе исследуется типовая задача определения согласованного механизма взаимодействия между заказчиком и подрядчиком путем выбора стимулирующей функции.
Проблема обоснования эффективности инвестиционных проектов в сложных условиях переходной экономики и повышенного риска, как на начальной стадии проектирования, так и на конечном этапе его реализации, является предметом пристального изучения и исследования зарубежных и отечественных ученых. Разработанные в настоящее время модели и методы многостадийной процедуры проектного анализа позволяют обосновать эффективность инвестиционного проекта на этапе проектирования. Однако эффективность их конечных результатов остается низкой в связи с отсутствием методики выбора механизмов их реализации. В мировой и отечественной практике накапливается опыт, создаются методологии и теоретические основы управления проектом в процессе его реализации. Сложность решения этой задачи состоит в том, что для успешного завершения проекта необходимо управление ходом выполнения работ, сроками, стоимостью, ресурсами. При участии в проекте нескольких исполнителей возникает проблема параметрического анализа выбранного проекта и решение на этой основе задачи согласованного их взаимодействия в процессе выполнения требований к качеству, срокам и объемам работ, установленных заказчиком. Решение этой задачи является предметом исследования теории активных систем, если в качестве активных элементов выступают заказчик, осуществляющий проектирование, и исполнитель – подрядчик, выполняющий совокупность взаимосвязанных работ. Актуальность работы состоит в том, что механизм управления проектом включает в себя процедуру планирования работ, на основе которой определяются оптимальные параметры проекта, и процедуру реализации их различными исполнителями, интересы которых могут быть не настроены на выполнение требований заказчика.
Учитывая сложность возникающей проблемы и то, что каждый проект является уникальным, в работе исследуется типовая задача определения согласованного механизма взаимодействия между заказчиком и подрядчиком путем выбора стимулирующей функции. В результате подрядчик становится заинтересованным в своевременном завершении проекта.
Основной идеей построения модели функционирования проекта, учитывающей активное поведение участников проекта, является включение в модель интересов исполнителей, участвующих в проекте, их целей, средств и методов достижения целей и результатов деятельности [1].
Для менеджера проекта и исполнителя в формализованном виде задачи выбора решений на этапе проектирования и реализации имеют следующий вид:
где x(n) и z(n) – плановый и фактический выпуск продукции в n-ом периоде,
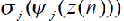- затраты исполнителя на выполнение j-ой работы в n-ом периоде,
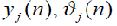– плановый и фактический объем j-ой работы выполненной исполнителем в n-ом периоде.
Менеджер проекта в результате решения задачи (1) определяет при фиксированной цене p(n) и стоимости единицы работы 
(n=0, …, N, j=1, …, J) оптимальный плановый объем выпуска продукции x*, оптимальные плановые объемы работ 
(n=0, …, N, j=1, …, J) и оптимальную величину целевой функции G*(x*). Исполнитель при тех же условиях в результате решения задачи (2)
устанавливает оптимальные фактические объемы работ 
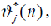(n=0, …, N, j=1, …, J) и соответствующий им
оптимальный фактический объем выпуска продукции z*(n), которые обеспечивают ему максимальное значение его целевой функции g*(z*(n)).
Плановые значения параметров проекта x*, y* представляют собой значения желаемые с позиции цели менеджера. Исполнитель на этапе реализации
плановых параметров проекта выбирает на своем допустимом множестве такие фактические параметры z(n),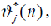
(n=0, …, N, j=1, …, J), которые обеспечивают ему достижение максимальной величины его целевой функции g(z). Будем считать, что цель
менеджера проекта реализована исполнителем, если исполнитель на этапе реализации проекта выбирает фактическое состояние проекта
z(n), 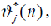равное плановому x*(n), , (n=0, …, N, j=1, …, J).
Из этого определения следует, что условием реализации оптимальных плановых значений параметров проекта является выполнение следующих равенств:
Для практической реализации условия (3) менеджер проекта должен согласовать экономические интересы исполнителя таким образом, чтобы он, реализуя свою локальную цель путем выбора фактических состояний, одновременно способствовал и реализации условия (3).
Обеспечить выполнение условия (3) можно путем выбора величины стимулирования, получаемой исполнителем при реализации им плановых значений параметров проекта. Величину стимулирования можно получить выбором специальной функции, зависящей от плановых и фактических значений параметров и являющейся переменной частью целевой функции исполнителя в задаче согласования экономических интересов.
Для решения задачи согласования интересов между менеджером проекта и исполнителем представим целевую функцию исполнителя в следующем виде:
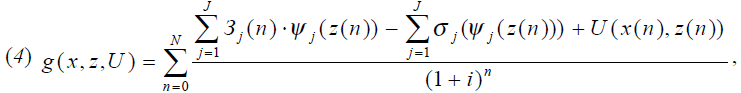
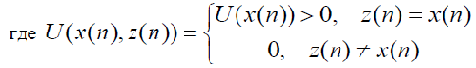– величина стимулирования, получаемая исполнителем в случае реализации им плановых значений параметров
проекта, установленных менеджером на основании своей целевой функции.
Для сбалансированности целей менеджеру проекта необходимо выбрать такую величину стимулирования, чтобы целевая функция исполнителя при реализации плановых значений параметров достигала значения не меньшего оптимальной величины, получаемой в результате решения задачи (2). Только в этом случае исполнитель будет настроен на выполнение плановых значений параметров, определенных менеджером.
Исходные задачи проектирования (1) и реализации оптимальных параметров (2) с учетом функции стимулирования (4) модифицируются в задачи следующего вида:
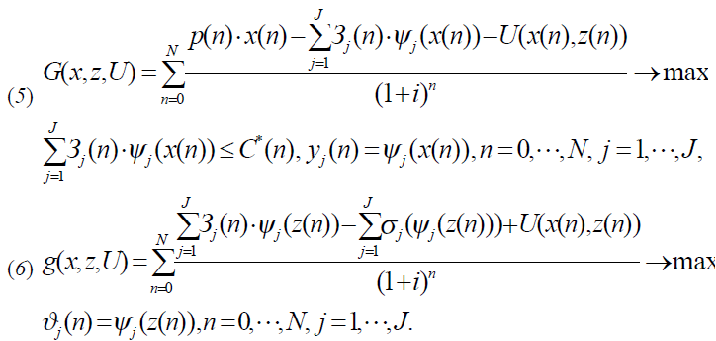
В результате совместного решения задач определяются такие значения стимулирующей функции, при которой максимум целевой функции менеджера G(x, z, U) и максимум целевой функции исполнителя g(x, z, U) достигаются для одних и тех же плановых значений параметров проекта. А это означает, что выполняется равенство между фактическими и плановыми значениями параметров.
Выбор значений функции стимулирования основывается на принципе компенсации затрат исполнителя при реализации им плановых значений проекта, выгодных для менеджера. В этом случае у менеджера проекта появляется дополнительный эффект, который он может использовать для стимулирования исполнителя за реализацию плановых показателей проекта.
Задача согласования взаимодействия может быть решена не только путем выбора специальной функции стимулирования исполнителя U(n), но и путем
изменения параметров, от которых зависит величина целевой функции исполнителя, например, стоимость единицы выполняемых им работ
(n=0, …, N, j=1, …, J). В этом случае задача по осуществлению согласованного взаимодействия между менеджером проекта и исполнителем
состоит в том, чтобы одновременно с определением оптимальных параметров проекта выдать такие значения стоимости работ, изменения которых
на величину (n=0, …, N, j=1, …, J) в каждом периоде приводило бы к компенсации потерь у исполнителя и выполнения условия (3). Решение
этой задачи определяется из следующей совокупности взаимодействующих моделей:
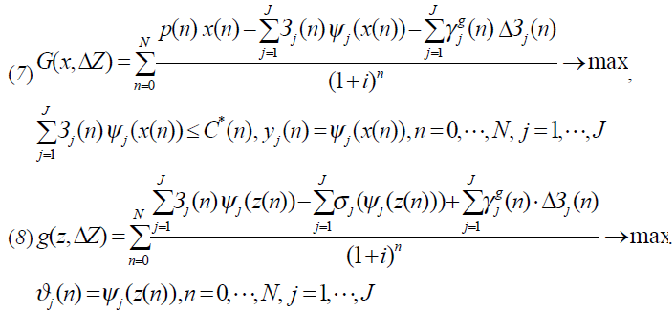
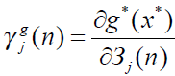– чувствительность целевой функции исполнителя, обеспечивающей максимум на этапе выбора
оптимальных параметров (2) еще без стимулирования, к изменению стоимости выполняемой им j-ой работы.
Совместное решение моделей (7)-(8) позволяет определить границы изменения договорной стоимости каждой работы и создать условия для экономической заинтересованности исполнителя в реализации оптимальных параметров проекта.
СПИСОК ЛИТЕРАТУРЫ