Источник: KSU факультет членов сайта
Авторы: GHARIEB* W., NAGIB** G.
Автор перевода с английского: Чепижко А.
SIMULINK БИБЛИОТЕКА НЕЧЁТКОЙ ЛОГИКИ
W. GHARIEB* Член IEEE, G. NAGIB**
* Доцент, компьютерных и инженерных систем отдела,
Инженерный факультет - Ain Shams университет,
1 El-Sarayat ул., 11517 Аббасия, Каир, Египет
Электронная почта: wahied@shams.eun.eg, факс: (202) 2850617
Доцент кафедры электротехники, инженерный факультет
Каирский университет - Fayoum отделение, Египет, факс: (202) 084 - 334 031
Аннотация: Эта статья представляет развитие нечеткой логики библиотеки с помощью динамического программное обеспечение для моделирования SIMULINK в среде MATLAB. Разработанные библиотеки включает основные блоки: MIN (минимальный режим), MAX (максимальный режим), MFG (Генератор функций принадлежности), FUZ (преобразование четкого ввода в нечеткие метки), F-правила (нечеткая матрица правил), F-INF (Min-Max нечеткого вывода), DEFUZ (получение чётких меток на выходе) и другие блоки, чтобы легко имитировать нечеткие системы. Разработанная библиотека нечеткой логики предоставляет дополнительные возможности для: образование нечетких понятий логики студентов технических специальностей, моделирование нечетких логических контроллеров с легкостью и проверкой аналоговой аппаратной реализации нечетких компонентов логики. Включены примеры моделирования, чтобы показать потенциал развитых Simulink библиотек нечеткой логики.
1. ВВЕДЕНИЕ
Нечёткая логика начальных работ Лотфи Заде А., который изобрел теорию нечетких множеств [1]. Нечеткая логика имеет два различных значения. В узком смысле это расширение многозначной логики. Но в более широком смысле, то это почти синоним теории нечетких множеств, теории, которая относится к классам объектов нечётких граници. В последнее десятилетие мы стали свидетелями стремительного роста количества и разнообразия приложений нечеткой логики. Приложений варьируются от потребительских товаров, таких как фотоаппараты, видеокамеры, стиральные машины, микроволновые печи до управления производственными процессами, медицинских приборов и систем поддержки принятия решений [2-3].
В этой статье, библиотека нечеткой логики разработана с использованием программного обеспечения для моделирования динамических системы Simulink 1.2, в среде MATLAB 4.0. SIMULINK построен на пакете MATLAB. Это программное обеспечение может предложить быстрый доступ к широкому выбору математических и технических методов для дальнейшего анализа динамических систем. Используя Simulink, новая библиотека добавляется для того, чтобы анализировать и проектировать нечеткие систем. Библиотека нечеткой логики осуществляется с помощью существующих линейных и нелинейных блоков библиотеки Simulink.
Выбор с использованием Simulink предлагает следующие преимущества:
Инструменты имеющие для нечеткой логики в MATLAB скрывают технические детали во время реализация упрощения моделирования взаимодействия с пользователями, которые знакомы и хорошо понимают нечеткую логику. Но для образования, это гораздо лучше понимать шаг за шаглм нечеткие блоки для реализации более высокого уровня функции, такие как нечеткий механизм вывода. Таким образом, моделирование с использованием разработанной нечеткой блочной библиотеки позволяет студентам и новичкам, узнать больше и больше о нечеткой логике.
Работа организована следующим образом: Раздел 1 представляет мотивацию для разработки нечеткой логики библиотеки Simulink. Раздел 2 посвящен развитию библиотеке нечеткой логики, где продемонстрированы основные блоки, детали и конструкции. В разделе 3, иллюстративные примеры, рассмотрение и представление нечеткого вывода и нечеткого логического контроллера. В завершении представлены некоторые замечания, приведённые в 4 разделе.
2. БИБЛИОТЕКА НЕЧЁТКОЙ ЛОГИКИ
Нечеткой логики библиотеки включает в себя следующие блоки, показанные на рис.1.
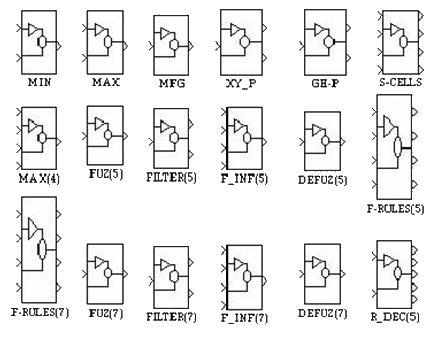
Рис.1. Логические блоки библиотеки нечёткой логики
Разработанная библиотека включает в себя следующие блоки:
| MIN | Вычисляет минимальный результат, входными данными являются 2 сигнала |
| MAX | Вычисляет максимальный результат, входными данными являются 2 сигнала |
| MAX (4) | Вычисляет максимальный результат, входными данными являются 4 сигнала |
| MFG | Генератор нечетких множеств |
| FUZ (5) | Элемент первичной обработки входных параметров для реализации методов нечёткой логики который отображает четкие входы с помощью 5 меток (NB, NS, ZE, PS, PB) |
| FUZ (7) | Элемент первичной обработки входных параметров для реализации методов нечёткой логики который отображает четкие входы с помощью 7 меток (NB, NM, NS, ZE, PS, PM, PB) |
| FILTER(5) | Выдаёт 2 смежных выходных ненулевых значений выхода fuzzifier FUZ (5) |
| FILTER(7) | Выдаёт 2 выходных смежных ненулевые значения выхода элемента первичной обработки входных параметров для реализации методов нечёткой логики FUZ (7) |
| F-RULES(5) | Справочная таблица, чтобы найти применимые нормы в правилах матрицы 5x5 |
| F-RULES(7) | Справочныя таблица, чтобы найти применимые нормы в правилах матрицы 7x7 |
| XY-P | Колонка указателей для ненулевых значений в матрице правил |
| GH-P | Строка указателей для ненулевых значений в матрице правил |
| R-DEC (5) | Определяет, выход в котором нечетко устанавливаются значение правила принадлежности |
| S-CELLS | Раздвижные клетки для определения применяемых 4 правила в матрице правил |
| F-INF (5) | Min-Max нечеткого вывода для формирования вектора из 5 выходных нечетких множеств |
| F-INF (7) | Min-Max нечеткого вывода для формирования вектора из 7 выходных нечетких множеств |
| DEFUZ (5) | Defuzzifier блок преобразования 5 выходных нечетких множеств в четкое значение |
| DEFUZ (7) | Defuzzifier блок преобразования 7 выходных нечетких множеств в четкое значение |
Вышеописанные блоки могут быть распространены на любое количество используемых нечетких множеств. Каждый блок параметров может быть введён легко с помощью маскировки возможности Simulink. В следующих подразделах продемонстрирован графическая наглядность основных блоков объясняющие основные идеи и показывающие детали реализации.
2.1 MIN блок
Этот блок предназначен для вывода минимального значения двух входных сигналов, как показано на рис.2.
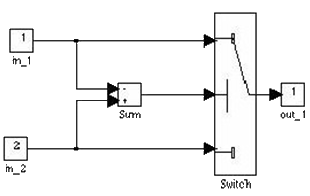
Рис.2. MIN блок-схема
Дизайн этого блока основан на использовании существующего блока переключателя в Simulink.
Переключатель блока позволяет выбирать сигнал между двумя сигналами. Если в переключателе второй вход больше или равна нулю, то первый вход (in_1) передается на выход. Если в переключателе второй вход
меньше нуля, то второй вход (in_2) передаётся на выход. Параллельные каскады блоков могут быть использованы для разработки MIN блока по числу входных сигналов более двух.
2.2 MAX блок
Этот блок предназначен для вывода максимального значения двух входных сигналов, как показано на рис.3.
Внешне он очень похож на MIN блок, но полярность у него противоположная. Параллельные каскадные блоки могут быть использованы для разработки блока MAX по числу входных сигналов больше двух. С помощью MAX (4) можно использовать до 4 входных сигналов.

Рис.3. Блок-схема MAX
2.3 MFG блок
MFG блок предназначен для получения функции принадлежности и вывода
значения подходящего класса. Этот блок может быть легко настроен для
получения любой частично-линейной характеристики, вида: треугольной, трапециевидной и одноплодной формы. Нечеткие множества
могут быть представлены с помощью одной из командр {NB, NM, Н.С., ZE,
PS, PM, PB}, используя MFG блок. Таким образом, элемент первичной
обработки входных параметров для реализации методов нечёткой логики
представляет собой массив из MFG
из нечетких множеств . На рис.4 представлена функция принадлежности
используемых нечетких множеств. Треугольную форму получают путем
настройки P2 = P3 , а одноплодная получается регулированием (Р1 =
Р4 и Р2 = Р3). Кроме того, эти параметры могут быть настроены для
получения любой фармы из нечетких множеств, сдвигая значения между
(-1, +1). Этот блок дает
положительные и отрицательные характеристики как показано на рис.4.
Положительная характеристика склонна создавать положительную часть,
которая может быть настроена путем изменения точки (P3 и P4) , а
также отсечением
элемента (насыщение блока) изменяя характеристики (0, 1). Отрицательная
характеристика создается путем изменения (P1 и P2) и отсечением
элемента (насыщением блока).
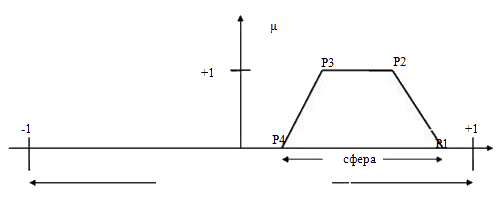
Рис.4. Членство функции
Полная характеристика получается с помощью Simulink, показана на рисунке 5. Для понятности:
Нижний предел насыщения = -1, Верхний предел насыщения = +1
Нижний предел насыщения 1 = 0, Верхний предел насыщения 1 = +1
Нижний предел насыщения 2 = 0, Верхний предел насыщения 2 = +1
Gain1 = 1 / (P3-P4) Const1 = P4 / (P3-P4)
Gain2 = -1 / (P1-P2), Const2 = P1 / (P1-P2)

Рис.5. Генератор функций принадлежности
2.4 FUZ блок
Этот блок используется для выполнения fuzzification интерфейса. fuzzification – размывание, подготовка задачи для решения методами нечеткой логики, перевод дискретных базисных объектов в непрерывные. Он преобразует входной сигнал в четкие подходящие языковые переменные, которые можно рассматривать в качестве меток нечетких множеств. На рис.6. показаны элементы первичной обработки входных параметров с использованием 5 нечетких меток NB, NS, ZE, PS, PB. Каждая из этих меток генерируется использованием MFG блока с apropriate настройками параметров P1, P2, P3 и P4. С помощью выхода для нечеткого мультиплексированного вектора можно легко сделать связь между другими ечеткими блоками.

Рис.6. Блок элемента первичной обработки входных параметров
2.5 DEFUZ блок
Этот блок используется для выполнения дефаззификации интерфейса. Он преобразует нечеткий вывод в четкое значение, используя управление методом. Этот метод принимает контроль действия значения, взвешивая по степени члены [4]. Рисунок 7 показывает концепцию дизайна использования поддержки значения пяти нечетких меток одноплодной MF (NB, NS, ZE, PS, PB). Они поддерживают значения, которые использует до пяти мультипликаторов в паре групп, где второй вход каждого множителя изменяет значение. Затем выходы из множителей можно разделить на сумму значений правил.
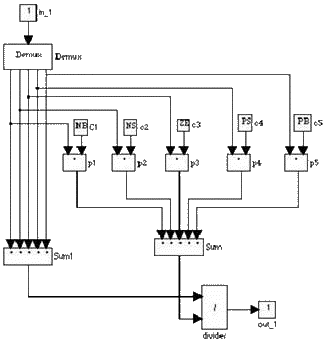
Рис.7. Defuzzifier блок (уменьшает нечеткости, но при этом он имеет большой минус, пользуясь данной системой теряется много времени для вычисления момента равновесия)
3. ПРИМЕРЫ МОДЕЛИРОВАНИЯ
3.1 Генератор функции принадлежности
В этом примере демонстрируется генератор функции принадлежности.
На рис.8. представлена блок-схема примера, в которой входной сигнал выбран в качестве повторяющихся
последовательностей графических изображений нормированного четкого входа между (-1, +1). Вход и выход сигналов MFG блока подключены к xy графа дисплея блок, где четкий вход (Повторяется последовательность) является х и выход из MFG является у. MFG маскируется, и пользователь может вводить параметры P1, P2, P3 и P4 и их изменения в процессе моделирования показывают, многие формы принадлежности (треугольные, трапециевидные, одиночные, ... и т.д.).
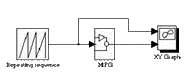
Рис.8 Генератор функции принадлежности
3.2 Нечёткий вывод
Концепция мин-макс нечеткого вывода показана на рис.9. Каждое четкое значение E ошибки и изменения DE , всегда представляется второй смежной ненулевой степенью значения и выходным вектором для подготовки задачи. Таким образом, вектор ошибки может быть подключен к входу (In_2), с помощью фильтра. Фильтр выводит 2 смежных ненулевые значения. Аналогичная операция выполняется на входе (in_3), который подключен к вектору DE. Тут могут быть применены только 4 правила, которые используют 2 строки и 2 столбца в матрице правил. S-клетоки блока определяют предпосылки значения каждой применимой операции, а просмотровые таблицы в F-блоках определяют правила соответствующего индекса метки (NB = 1, NS = 2, ZE = 3, PS = 4, PB = 5). Массив декодеров используются для подключения каждого правила к блоку MAX соответствующей выходной нечеткой метке. Наконец, все выходы легко подключаться к этому блоку в различных приложениях.

Рис.9. Нечеткий блок вывода
3.3 Нечеткий контроллер
Нечеткий контроллер в основном состоит из 4 блоков, как показано на рис.10:
FUZ блок выдаёт E сигнал ошибки
FUZ блок выдаёт ошибку изменения DE
F-INF блоков для генерации нечеткого выхода контроллера
DEFUZ блок создаёт четкий выход
Три метки GE, GDE, ГУ используются для масштабирования входных и выходных сигналов в соответствии с приложениями, где основная структура контроллера использует значения в промежутке (-1, +1).

Рис.10. Нечеткая структура контроллера
4. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Библиотека нечёткой логики предоставляет следующие возможности для:
• Курса образования основ нечеткой логики у студентов технических специальностей, для понятия и доказания теории нечетких множеств через группу экспериментов, таких как,
- Изучение различных функций принадлежности
- Внедрение вектора четких переменных в определенной степени
- Реализация нечеткого вывода
- Изучение различных методов нечеткой логики
- ... И т.д.
• Моделирование нечеткого логического контроллера и проверка его эффективности на различных динамических моделях с использованием графического редактора Simulink для реализации замкнутой системы.
• Реализация аналоговых устройств и их проверка функций на работоспособность [5].
Ссылки
| [1] | L. A. Zadeh , "Нечёткие множества", Информация и управление., Vol.8, pp.338-353, 1965. |
| [2] | J. Maiers and Y. S. Sherif, "Применение теории нечетких множеств", IEEE Trans. на системе, Человек и кибернетика, Vol. SMC-15, № 1, январь. / Февраль 1985 год. |
| [3] | H.-J Zimmermann "Теории нечетких множеств и ее приложения", Kluwer Academic Publishers, 2-е издание, 6-й печати, 1993 год. |
| [4] | C.C. Lee, "Нечёткая логика в системах управления: нечётких логических контроллеров, часть II", IEEE Trans. Syst. Человек. Кибернетики., Vol.20, № 2, pp.419-435, 1990. |
| [5] | В. Gharieb, "Оборудование нечеткой логики Design Kit", 6 Int IEEE. Конф. по нечетким системам, vol.n ° 2/3, pp.1039-1043, Барселона Испания, 1-5 июля 1997 года. |