Автор: Фатов А.В., Черненко В.А., Приходько С.Ю., Лунева О.В.
Источник:Збірник матеріалів до регіональної наукової конференції аспірантів і студентів «Екологічні проблеми топливно – енергетичного комплексу»,
(18 – 19 травня 2010 р, Донецьк): Зб. матер. конф./ ред. О.В. Луньова, В.Г. Ефімов – Донецьк, ДонНТУ, 2010р. – 39-44 с.
Система работает системно (оптимально), если каждый отрезок системы максимально информирован друг о друге и об окружающем пространстве. При такой работе системы каждый ее отрезок выполняет оптимальную работу поддержания своей жизнеспособности и всей системы в целом. Если отрезок системы минимально информирован, он работает в разном ритме с системой, то есть против системы. С помощью компьютерных программ можно точно диагностировать любую экосистему, отслеживать ее динамику и устойчивость с помощью коэффициента системности.
В работе рассматриваются вопросы по оценке качества функционирования систем. Указывается возможность широкого применения полученных результатов: для диагностики, для решения многокритериальных задач и т.д.
Для исследования динамики и критериев устойчивости экосистем была разработана программа, алгоритм которой приведен на рис.1.
Рис.1. Алгоритм программы.
Принцип работы программы изложен на Рисунке 2: поэтапное преобразование матрицы исходных данных X.
На рисунке 2 обозначено:
X – матрица исходных данных размерностью n*m (n – число наблюдения, m – число элементарных признаков);
Z – матрица центрированных и нормированных значений признаков, элементы матрицы вычисляют по формуле: zi,j =(xi,j-x‾j)/σj;
R – матрица парных корреляций: R=(1/n)*Z ’*Z.
Шаги вычислений для метода главных компонент:
Λ – вектор собственных (характеристических) чисел.
КС- коэффициент системности, вычисляемый по формуле
КС = Λ[1]/sum(Λ)
Рис. 2. Схема математических преобразований.
На рисунке 3 показан интерфейс программы в том виде, в котором она была подготовлена для исследования экосистемы
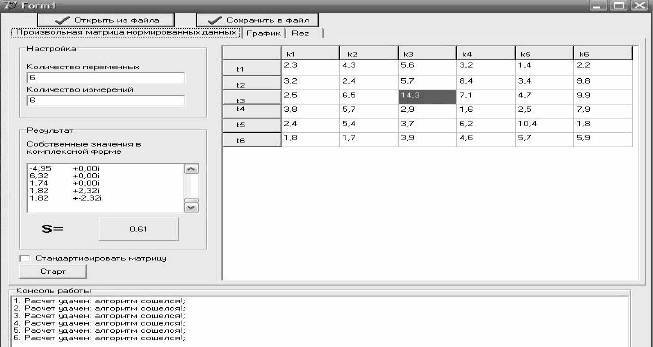
Рис. 3. Интерфейс программы для исследования экосистем. k1... k6 - параметры системы. t1... t6 - временные интервалы.
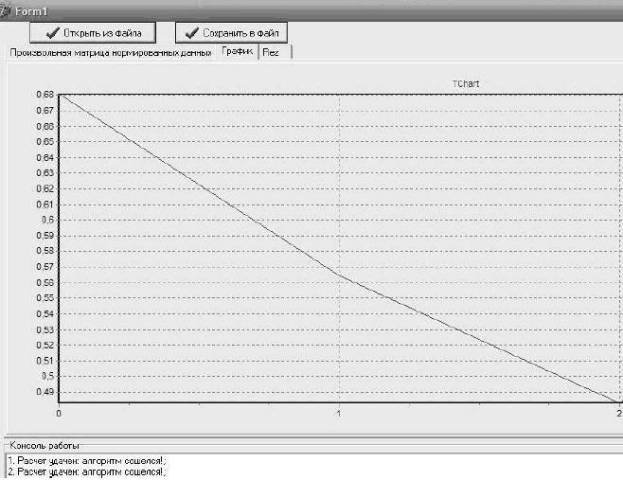
Рис. 4. Динамика коэффициента системности ( система не устойчива, коэффициент системности стремится к 0)
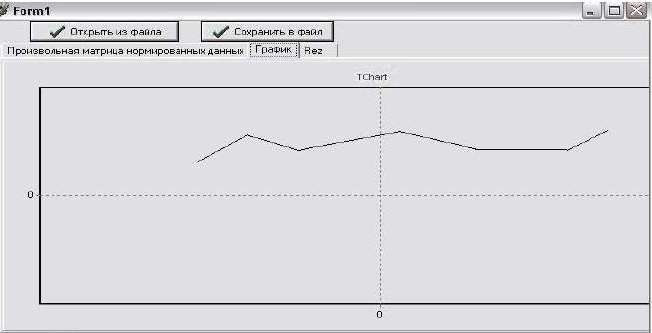
Рис.5. Динамика поведения коэффициента системности( система устойчива, коэффициент системности практически постоянен)
Вывод значений коэффициента системности:
S = 0,61
Max1 = 9,3
Max2 = 8,4
Max3 = 7,9
Max4 = 7,1
S = 0,62
Max1 = 9,3
Max2 = 8,8
Max3 = 8,4
Max4 = 7,1
S = 0,63
Max1 = 8,8
Max2 = 7,1
Max3 = 6,5
nоMax4 = 6,2
Дальнейшее усовершенствование программы позволит производить весовую оценку параметров системы в определенные интервалы времени и определять долю их влияния на динамику и устойчивость системы.
1. Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности . М., 1989.
2. Садовский М.А., Писаренко В.Ф. О прогнозе временных рядов // Пределы предсказуемости. М., 1997.