Дашкевич Д.О., Секирин А.И. – Моделирование системы массового обслуживания перевозки пассажиров

Аннотация

Мы представляем систематическую обработку эффективной нелинейной оптимизации систем массового обслуживания. Набор формулировки использует вычислительный инструмент оптимизации выпуклых, с быстрыми алгоритмами за полиномиальное время, чтобы получить глобальный оптимум для этих нелинейных задач при различных ограничениях. Сначала покажем, выпуклости структуры нескольких систем массового обслуживания, в том числе некоторые уникальные переходы, а затем разработку и показ численных примеров нескольких выпуклых оптимизаций производительности очередей сетей обслуживания. Также представлены блокирование минимизации вероятности и распределения скорости обслуживания за счет эффективного подхода пропускной способности.

Введение

Очередь системы образуют фундаментальную роль для различных типов сетей, в том числе многопроцессорной вычислительной сети и коммуникации сетей передачи данных. Очередь системы также является неотъемлемой частью различных элементов сети, например, входной и выходной буферы с коммутацией пакетов. Мы часто хотим оптимизировать некоторые показатели эффективности систем массового обслуживания, например, размещение буфера, общая задержка, колебания, нагрузки. В сети очередей, мы можем иметь множество противоречивых целей, которые должны быть оптимально сбалансированы. Тем не менее, оптимизация производительности, даже простой очереди, как M/М/м/м очереди вообще трудная задача из-за нелинейности показателей производительности в зависимости от прибытия и тарифами на услуги. Нелинейная оптимизация в целом занимает время работы, которое масштабируется экспоненциально с ростом размера задачи.

Мы покажем, как выпуклость свойства систем массового обслуживания могут быть использованы, чтобы включить некоторые из этих неразрешимых проблем в полиномиальное время разрешимых. Используя инструмент оптимизации выпуклой, и, в частности, геометрическое программирование, мы предлагаем набор формулировок, чтобы эффективно оптимизировать производительность систем массового обслуживания по качеству обслуживания (QoS) и справедливость ограничения, для блокирования минимизации вероятности и распределения скорости обслуживания за счет эффективного подхода пропускной способности, для сетей очередей, и для оптимального управления с обратной связью в простых сетях массового обслуживания. Отличительные особенности формулировок в этой работе является то, что они нелинейные проблемы, которые могут быть решены так же легко, как линейных задач с помощью выпуклой оптимизации.

Выпуклая оптимизация и геометрическое программирование

Выпуклая оптимизация относится к минимизации выпуклой функции предмета целью верхней границы неравенства на выпуклых функций ограничений. Целевая функция может быть обобщена для векторных, где минимизация по отношению к выпуклым является конусом. Эти выпуклые полезны для анализа компромиссов, а понятие оптимальности теперь становится оптимальностью по Парето.

Выпуклые задачи оптимизации можно легко решить, как в теории и на практике. Теоретически, показывая задачи оптимизации строго выпуклыми они показывают, что существует единственное глобальное оптимальное решение, и приводит к выполнению оценки и анализу чувствительности по двойственной задаче. Практически, если положить в нужной форме, выпуклая оптимизация может быть глобально решена быстрыми алгоритмами за полиномиальное время. Это также дает хорошую отправную точку для разработки еще более простой эвристики и устанавливает оптимальный ориентир для сравнения с эвристики.

Оптимизация для средней задержки и очереди размещение

Мы начинаем набор формулировок выпуклой оптимизации с простого примера минимизации службы нагрузка в M/М/1 очереди с ограничениями на среднюю задержку очереди W, общую задержку D, и очереди размещение Q.

Следующие нелинейноые оптимизации геометрических программы, и, следовательно, могут быть превращены в выпуклую оптимизацию и эффективно решить ее нахождением глобального оптимума.

Рисунок 1 – Набор формулировок выпуклой оптимизации

где оптимизация переменных скорость прибытия λ и скорость обслуживания μ. Постоянные параметры производительности верхней границы Wmax, Dmax и Qmax и практические ограничения на максимальную скорость службы очереди μ max, которые не могут быть превышены, а минимальная скорость входящего трафика λ min, которые должны быть поддержаны. Цель состоит в том, чтобы минимизировать услуги нагрузки.

Можно также показать, что даже совместное оптимизации по обоим (λ,μ) и (Wmax, Dmax, Qmax) до сих пор геометрическая программа.

Приведенная выше формулировка может быть расширена до Марковского представления системы массового обслуживания с очередями N совместного пула скорости обслуживания ограниченного μ max (например, связанные с общей исходящей скоростью связи). Скорость прибытия в поддержке для каждой очереди i ограничена λi,min. Есть задержки и очереди размещение границы Wi,max, Di,max и Qi,max для каждой очереди i. Целью теперь становится минимизации взвешенной суммы эксплуатационных нагрузок для всех очередей:

Следующей нелинейной оптимизации геометрической программы:

Рисунок 2 – Набор формулировок выпуклой нелинейной оптимизации

где оптимизация переменных скорости поступления λi и тарифами на услуги μi.

Оптимизация M/M/м/м очереди

Теперь оптимизировать конкретные вероятности занятия очереди, сначала рассматривает М/М/м/м очереди.

Устойчивая вероятность состояния к задается как:

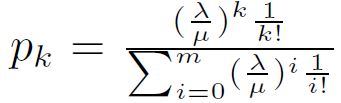
Рисунок 3 – устойчивая вероятность состояния

Во многих приложениях систем массового обслуживания для проектирования сети, мы хотели бы максимизировать вероятность определенного желательного состояния, без вероятности других состояний.

Например, мы хотим создать телефонную колл-центра так, чтобы максимизировать вероятность того, что определенное количество телефонных линий (например, 90%) приходится на использование в любой момент времени. Мы также хотим совместно оптимизировать Cj справедливости параметров, границы Pj.

Следующие нелинейной оптимизации М/М/м/м очереди представляет собой геометрическую программу:

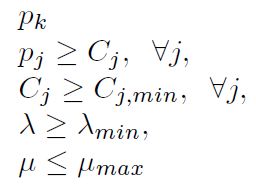
Рисунок 4 – Нелинейная оптимизация М/М/м/м очереди

где оптимизация переменных λ,μ и Cj, а постоянное параметры λ min, μ max и справедливости ограничений Cj,min, j=1,2,…,m.

Эта геометрическая формулировка программирования может быть продлена до максимальной вероятности для состояния с низкой вероятностью исполнения максиминными справедливостью. Подобные формулировки можно сделать для параллельной M/М/м/м очереди и общей M/G очереди.

Вывод

На основе различных результатов о выпуклых свойствах систем массового обслуживания и вычислительнию эффективных алгоритмов для оптимизации выпуклой, мы представляем набор формулировок, чтобы оптимизировать производительность одной очереди, сетей очередей и больших границах теоретического отклонения на вероятность блокировки минимизации. Эти нелинейные оптимизации производительности могут осуществляться на глобальном уровне в полиномиальное время для сетевых систем массового обслуживания QoS и по справедливости ограничений.

Список литературы

S. Boyd and L. Vandenberghe, Convex Optimization Stanford University EE 364 Course Reader 2001.
C. S. Chang, Stability, queue length and delay of deterministic and stochastic queuing networks IEEE Trans. Automatic Control, vol. 39, pp. 913–931, 1994.
M. Chiang and S. Boyd, Shannon duality through Lagrange duality: efficient computation and free energy interpretations for channel capacity and rate distortion, Proc. 40th Allerton Conference, Oct. 2002.
R. J. Duffin, E. L. Peterson, C. Zener, Geometric Programming: Theory and Applications, Wiley 1967.
J. Y. Hui, Resource allocation for broadband networks, IEEE J. Sel. Area Comm., pp.1598–1608, 1988.
D. Julian, M. Chiang, D. O’Neill, and S. Boyd, QoS and fairness constrained convex optimization of resource allocation in wireless cellular and ad hoc networks, Proc. IEEE Infocom, New York, June 2002.
F. P. Kelly, Notes on effective bandwidth, Stochastic Networks: Theory and Applications, pp.141–168, Oxford Unviersity Press, 1996.
L. Kleinrock, Queueing Systems, vol.I, Wiley, 1974.

Эффективная оптимизация нелинейных систем массового обслуживания