Назад в библиотеку
Проектирование СКС диагностики сердечно-сосудистых заболеваний
Авторы: Е.В. Дашутина, Е.В. Меркулова
Источник: Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС КМ-2012) – 2012 / Матерiали II мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2012, с. 285–288.
Аннотация
Дашутина Е.В., Меркулова Е.В. Проектирование СКС диагностики сердечно-сосудистых заболеваний. Описаны особенности существующих систем стратификации риска и ранней диагностики сердечно-сосудистой патологии. Проанализированы методы определения информативности. Определена структура СКС.
Введение
Сердечно-сосудистые заболевания (ССЗ) являются основной причиной смерти во всем мире. По оценкам, в 2008 году от ССЗ умерло 17,3 миллиона человек, что составило 30% всех случаев смерти в мире. Из этого числа 7,3 миллиона человек умерло от ишемической болезни сердца и 6,2 миллиона человек в результате инсульта.
Едва ли не важнейшей целью медицинских исследований является классификация объекта или применительно к пациенту и заболеванию – диагностика. Постановка диагноза может быть сформулирована, как математическая задача, а следовательно автоматизирована.
Общая постановка проблемы
Основная задача заключается в разработке проблемно-ориентированной системы анализа статистической медико-биологической информации (далее признаков) больных ССЗ с целью прогнозирования или предупреждения риска заболевания диагностируемого пациента. Под анализом подразумеваем определение информативности признака, которая означает, насколько данный признак характеризует психофизическое состояние объекта (пациента), то есть насколько от данного признака зависит постановка диагноза.
Что бы подтвердить актуальность проектируемой СКС, рассмотрим некоторые особенности имеющихся на данный момент достижений в области оценки информативности:
- большинство методик разрабатываются для конкретных заболеваний, и часто оказываются непригодными для ряда других;
- анализ данных ведется статистическими методами, а большинство выводов статистических исследований делается при условии нормальности распределений данных, что не справедливо для всех медико-биологических показателей;
- недостаточно хорошо изучена значимость многих факторов, оказывающих влияние на постановку диагноза, и часто в исследованиях изучаются лишь те признаки, которые, по мнению врача, наиболее явно отражают заболевание;
- из-за сложности обработки данных не всегда применяются наиболее мощные критерии и медики ограничиваются, например, линейным приближением или степенным уравнением.
Приблизительная структура СКС представлена на рис.1. Входными данными СКС будет являться база данных Донецкой больницы профзаболеваний. В структуру СКС войдут все блоки расположенные ниже блока «База данных». Основным блоком проектируемой СКС является «Блок обработки». В этом блоке предполагается выполнить выборку признаков с последующим расчетом их информативности.
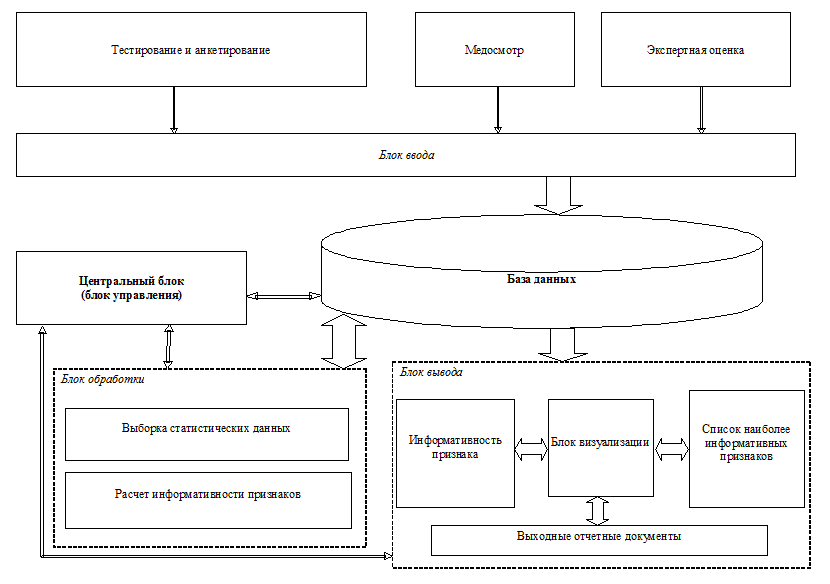
Рис.1. Структура разрабатываемой СКС
Математические методы
Метод определения информативности выбирает сам исследователь в зависимости от целей исследования, количества распознаваемых классов и медико-биологических данных – способа кодировки, объема выборки количества градаций.
Существует, по меньшей мере, 2 подхода к оценке информативности – энергетический и информационный. Энергетический подход основан на том, что информативность оценивается по величине признака. Однако, если какой-то признак велик по абсолютной величине, но почти одинаков у объектов различных классов, то по значению этого признака трудно отнести объект к какому-то классу. И наоборот – если признак относительно мал по величине, но сильно отличается у объектов разных классов, то по его значению можно легко классифицировать объект. Поэтому более пригодным для распознавания объекта является информационный подход, согласно которому информация признака рассматривается, как достоверное различие между классами образов в пространстве признаков. Если при распознании объекта его нужно отнести к одному из 2-х классов, то в качестве такого достоверного различия может выступать различие распределений вероятностей признака, построенных по выборкам из 2-х сравниваемых классов.
Оценкой информативности служит величина I(xj) - площадь одного распределения признака xj, не общая с площадью другого распределения этого же признака.
Метод накопленных частот (МНЧ). Сущность этого метода состоит в том, что если имеются 2 выборки признака х, принадлежащие 2-м различным классам, то по обеим выборкам в одних координатных осях строят эмпирические распределения признака х и подсчитывают накопленные частоты (сумму частот от начального до текущего интервала распределения). Оценкой информативности служит модуль максимальной разности накопленных частот.
Метод Шеннона. Предлагает оценивать информативность как средневзвешенное количество информации, приходящиеся на различные градации признака. Под информацией в теории информации понимают величину устраненной энтропии.
Итак, информативность j-ого признака:
 |
(1) |
G – количество градаций признака;
K – количество классов;
Pi – вероятность i-той градации признака.
 |
(2) |
mi,k – частота появления i-той градации в К-том классе;
N – общее число наблюдений.
Pi,k – вероятность появления i-той градации признака в К-том классе.
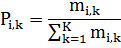 |
(3) |
Метод Кульбака. Предлагает в качестве оценки информативности меру расхождения между двумя классами, которая называется дивергенцией.
Согласно этому методу информативность или дивергенция Кульбака вычисляется по формуле:
 |
(4) |
G – число градаций признака;
Pi1 – вероятность появления i-той градации в первом классе.
 |
(5) |
mi1 – частота появления i-той градации в первом классе;
Знаменатель – появление всех градаций в первом классе, то есть общее число наблюдений в первом классе.
Pi2 – вероятность появления i-той градации во втором классе.
 |
(6) |
mi2 – частота появления i-той градации во втором классе.
Для того чтобы определить способ оценки информативности признака был проведен сравнительный анализ трех выше изложенных методов.
- Зависимость методов от способа кодировки признака.
МНЧ зависит от способа кодировки признака, методы Шеннона и Кульбака – не зависят от способа кодировки.
- Зависимость методов от числа классов.
МНЧ и метод Кульбака служат для определения информативности признака, который участвует в распознавании только двух классов объектов. Метод Шеннона позволяет определить информативность признака, участвующего в распознавании произвольного числа классов объектов.
- Зависимость методов от числа градаций признака.
Все три метода не зависят от числа градаций признака.
- Зависимость методов от объема выборки.
Так как МНЧ оперирует частотами, то объем выборки наблюдений признака должен быть одинаков по обоим распознаваемым классам. Методы Кульбака и Шеннона оперируют вероятностями, поэтому объемы выборки наблюдений признака по двум распознаваемым классам могут быть различны.
- Зависимость методов от объема вычислений.
МНЧ - проще по объему вычислений. Методы Кульбака и Шеннона – сложнее.
- Универсальность методов или зависимость от абсолютной величины информативности.
Информативность, определяемая всеми тремя методами – величина положительная, однако в МНЧ и методе Кульбака она не является нормированной, поэтому об информативности, определенной этими методами можно говорить только в относительном плане – более высокая или более низкая по сравнению с информативностью другого признака. Метод Шеннона дает оценку информативности, как нормированной величины, которая изменяется от 0 до 1. поэтому об информативности признака, определенной методом Шеннона можно говорить в абсолютном плане: ближе к 1 – высокая; ближе к 0 – низкая.
Какой бы из способов ни применялся, если информативность всех признаков оценивать одним и тем же способом, то можно выбрать более информативные и отбросить менее информативные признаки для постановки конкретного диагноза. Для разрабатываемой СКС предусматривается применение метода Кульбака.
Выводы
Едва ли не важнейшей целью медицинских исследований является классификация объекта или применительно к пациенту и заболеванию – диагностика. Проектируемая СКС предполагает обработку статистических данных, а именно медико-биологических показателей путем определения их информативности, после чего выбора наиболее информативных для упрощения дальнейшей диагностики пациента.
На основе поставленных целей и задач сформирована структура разрабатываемой СКС. Рассмотрены методы реализации основной задачи – оценки информативности признаков. Проведен сравнительный анализ рассмотренных методов.
Список использованной литературы
1. Генкин А.А. Новая информационная технология анализа медицинских данных; Программный комплекс ОМИС / А. А. Генкин. – СПб. : Политехника, 1999. – 191 с.
2. Гублер, Е. В. Применение непараметрических критериев статистики в медико-биологических исследованиях / Е. В. Гублер, А. А. Генкин – Л.: Медицина, 1973. – 144 с.
3. Давнис В.В. Прогнозные модели экспертных предпочтений: монография / В.В. Давнис, В.И. Тинякова. – Воронеж: Изд-во Воронеж. гос. ун-та, 2005. – 248 с.