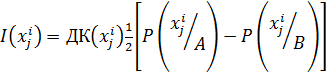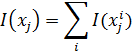Назад в библиотеку
Разработка и реализация алгоритма оценки информативности признаков при диагностике заболеваний
Автор: Дашутина Е.В., Блощицкий В.П.
Источник: Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС КМ-2011) – 2011 / Матерiали II мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2011, с. 17–19.
Аннотация
Дашутина Е.В., Блощицкий В.П. Разработка и реализация алгоритма оценки информативности признаков при диагностике заболеваний. Рассмотрен статистический критерий оценки информативности признаков. Определены преимущества оценки меры расхождения между распределениями, соответствующими двум выборкам, по критерию Кульбака. Составлен алгоритм нахождения величины информативности. Разработана база данных для реализации алгоритма.
Общая постановка проблемы
При изучении объектов, характеризуемых большим числом факторов, часто бывает важно определить, какие из этих факторов в большей степени влияют на интересующие нас свойства объектов. В частности, определение информативности факторов – это один из важных этапов анализа изучаемого объекта. В отличие от других критериев статистической значимости различий, мера Кульбака позволяет оценить не достоверность различий между распределениями, а степень этих различий. Метод анализа признаков путем оценки информативности критерием Кульбака получил широкое применение в медицине, при рассмотрении отдельных факторов, влияющих на постановку диагноза.
Исследования
Под дифференциальной информативностью признака понимают степень различий его распределений при дифференцируемых состояниях А и В. Эти состояния, хранимые в БД в виде статистических данных, являются входными данными.
Первым шагом в разработке алгоритма, производящего вычисление информативности признака, является разбиение интервала статистических данных на диапазоны. Для этого выбираем такие равные между собой диапазоны, чтобы их количество составляло 10. В алгоритме, для получения длины диапазона, производится выбор максимального и минимального значения из всего ряда с последующим делением этого отрезка на 10.
Следующий шаг алгоритма – подсчет числа наблюдений из групп А и В, попавших в данный диапазон. Это частоты данного признака. Затем находим частости путем представления полученных частот в процентах, принимая за 100% сумму частостей А во всех диапазонах и такую же сумму частостей В.
На следующем шаге алгоритма вычисляют сглаженные (средневзвешенные) частости для большинства диапазонов по формуле:
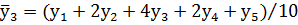
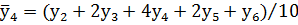 |
(1) |
и т.д., где 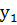 – член выборки, ближайший к любому ее краю;
– член выборки, ближайший к любому ее краю;
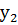 – второй от края член выборки;
– второй от края член выборки;
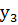 – третий от края и т.д.;
– третий от края и т.д.;
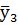 и
и 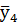 – «средневзвешенный» или «сглаженный» член выборки.
– «средневзвешенный» или «сглаженный» член выборки.
Для крайних диапазонов №1, 2 и 9, 10 – по формулам:
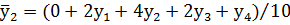 |
(2) |
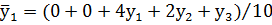 |
(3) |
Наглядно данный расчет представлен в виде блок-схемы на рис. 1.
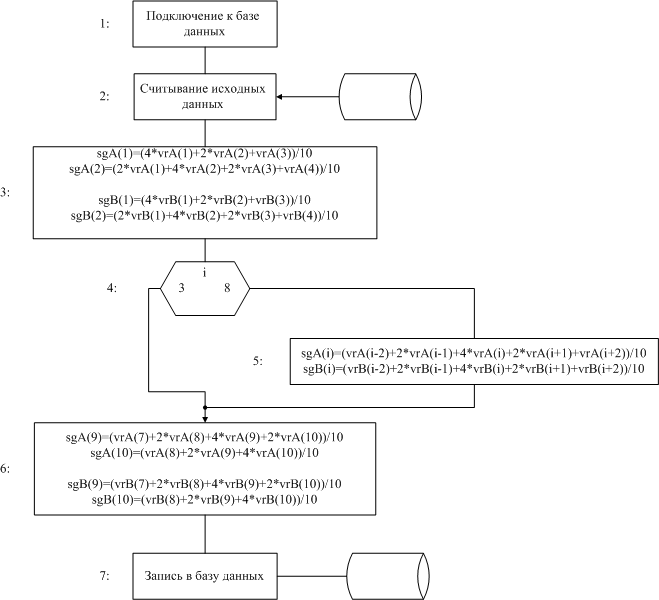
Рис. 1. Блок-схема алгоритма расчета сглаженных частостей для каждого диапазона
Массивы sgA и sgB предназначены для хранения результатов, а именно сглаженных частостей состояний А и В соответственно. Массивы vrA и vrB получены на предыдущем этапе расчета, они хранят относительные частости попадания в диапазон. В блоках 3 и 6 производится расчет согласно формулам (2) и (3). В цикле в блоке 5 расчет ведется по формуле (1).
Следующим этапом в разработке алгоритма является вычисление отношений сглаженных частостей А и В в каждом диапазоне, полученных на предыдущем этапе.
Теперь переходим к вычислению диагностических коэффициентов по формуле:
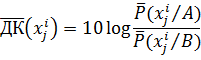 |
(4) |
где 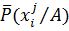 и
и 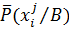 – средневзвешенные частости признака в каждом диапазоне. Все полученные величины диагностических коэффициентов округляют с точностью до единицы.
– средневзвешенные частости признака в каждом диапазоне. Все полученные величины диагностических коэффициентов округляют с точностью до единицы.
Последний этап – вычисление информативности каждого диапазона. Согласно формуле Кульбака величина информативности I диапазона i признака j равна:
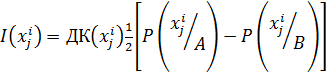 |
(5) |
Информативность всего признака xj равна сумме информативностей его диапазонов:
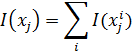 |
(6) |
Все расчеты, кроме расчета сглаженных частостей, производятся последовательно, учитывая данные текущего диапазона.
Для хранения исходных данных и полученных результатов была разработана база данных, физическая модель которой представлена на рис. 2.
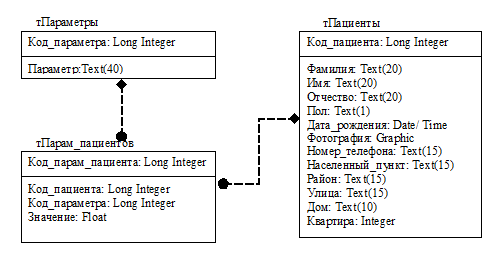
Рис. 2. Физическая модель данных
Выводы
На основе вероятностных подходов с использованием методики расчета информативности по Кульбаку сформирован алгоритм создания и расчета словаря диагностических признаков.
Алгоритм прошел проверку на данных кардиологического отделения Областной клинической больницы профзаболеваний. Таким образом, реализация рассмотренного алгоритма обеспечивает сокращение трудозатрат при высокой точности расчетов.
Список использованной литературы
1. Генкин А.А. Новая информационная технология анализа медицинских данных; Программный комплекс ОМИС / А. А. Генкин. – СПб. : Политехника, 1999. – 191 с.
2. Гублер, Е. В. Применение непараметрических критериев статистики в медико-биологических исследованиях / Е. В. Гублер, А. А. Генкин – Л.: Медицина, 1973. – 144 с.
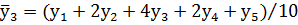
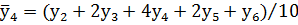
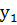 – член выборки, ближайший к любому ее краю;
– член выборки, ближайший к любому ее краю;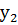 – второй от края член выборки;
– второй от края член выборки;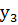 – третий от края и т.д.;
– третий от края и т.д.;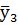 и
и 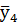 – «средневзвешенный» или «сглаженный» член выборки.
– «средневзвешенный» или «сглаженный» член выборки.
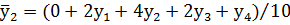
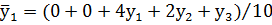

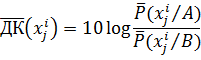
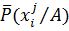 и
и 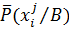 – средневзвешенные частости признака в каждом диапазоне. Все полученные величины диагностических коэффициентов округляют с точностью до единицы.
– средневзвешенные частости признака в каждом диапазоне. Все полученные величины диагностических коэффициентов округляют с точностью до единицы.