Драгун И.А. - Поддержка принятия решений при операциях у больных механической желтухой

Принятие решения о проведении хирургического вмешательства, прогнозирование его исхода и эффективности зависят от адекватности оценки операционного риска.

Исходя из неоднозначности характера процесса развития заболеваний, для оценки операционного риска и прогнозирования исхода операции нами избран вероятностно – статистический подход [3, 5]. Этот выбор по существу соответствует теоретическим концепциям биокибернетики и общей теории систем, согласно которым организм человека и высших животных относятся к очень сложным, вероятностным по своей природе системам [3, 5, 6].

Вероятностная модель чаще всего строится на теореме Байеса и ее приложениях. Применительно к состояниям больных, формула Байеса позволяет рассчитать вероятность каждого из возможных состояний, если обнаружен определенный набор биоединиц и известны общие (априорные) вероятности состояний. Под биоединицами и биопоказателями мы понимаем симптомы болезни, результаты лабораторных тестов и инструментальных методов исследования, характеризующих состояние больного [3, 4]. В общем виде формула Байеса представляется следующим выражением [1, 3, 4]:

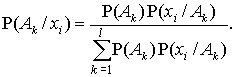(1)

Здесь и далее обозначения следующие: P(A_k / x_i) – вероятность состояния A_k при наличии биоединицы x_i; P(A_k) – априорная вероятность состояния A_k; P(x_i / A_k) – условная вероятность биоединицы x_i при состоянии A_k; l – общее число рассматриваемых состояний.

Часто на практике установить характер распределения величин и аппроксимировать их известными теоретическими распределениями довольно сложно. Поэтому для применения формулы Байеса выборки биопоказателей разбивают на диапазоны и вычисляют условные вероятности биоединиц в диапазонах для каждого из возможных состояний больного. Также используют предположение о независимости между собой всех биопоказателей, хотя применительно к живому организму данное предположение, строго говоря, маловероятно. По-видимому, даже если использовать зависимые биопоказатели, предположение об их независимости в большинстве случаев вносит меньшие искажения, чем те, которые связаны со случайными флуктуациями в диапазонах при малых объемах выборок [2, 3, 4]. Формула Байеса для комплекса независимых биоединиц, значения которых попадают в диапазон с номером j, имеет следующий вид:

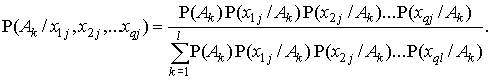(2)

При рассмотрении двух альтернативных состояний больного полезно вычислять отношение вероятностей этих состояний для каждого биопоказателя. В статистике данное отношение называют отношением правдоподобия, так как оно показывает насколько одна гипотеза правдоподобнее другой при определенных условиях. Для случая равных априорных вероятностей отношение правдоподобия состояний равно отношению условных вероятностей биоединиц при этих состояниях [1, 3]:

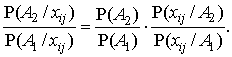(3)

На использовании отношений правдоподобия и возможности учета диагностических ошибок, основана Неоднородная Последовательная Процедура (НПП). НПП, впервые предложенная А.А. Генкиным в 1962 г., является разновидностью последовательного анализа Вальда для неоднородной информации. Суть её заключается в следующем. Последовательное умножение отношений правдоподобия биоединиц при двух альтернативных состояниях A₁ и A₂ прерывают по достижению диагностических порогов, которые намечают, исходя из заранее выбранного теоретически - допустимого уровня диагностических ошибок [2, 3]:

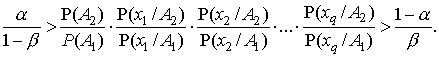(4)

При превышении одного из диагностических порогов процедуру останавливают и принимают одно из решений: «Состояние A₁», «Состояние A₂» или «Имеющейся информации недостаточно для принятия решения с намеченным уровнем надежности». Диагностические пороги находят исходя из теоретической возможности ошибок первого и второго рода, обозначаемых α и β соответственно.

Ошибка первого рода – α – происходит когда крайне тяжёлое угрожающее состояние A₂ можно принять за менее тяжелое A₁. Ошибка второго рода – β – происходит когда при менее тяжелом состоянии A₁ ставят ошибочный диагноз более тяжелого состояния A₂ [2, 3, 4].

Опасность этих ошибок может быть неодинакова. Очень часто ошибка первого рода α – пропуск крайне тяжелого состояния A₂ – более опасна, чем β – его ошибочная диагностика. В таком случае желательно, чтобы при Неоднородной Последовательной Процедуре был обеспечен меньший уровень ошибок первого рода.

Наиболее быстрый ответ и наименьшее количество ошибок будет допущено, если начать процедуру с тех биоединиц, распределения вероятностей которых при состояниях A₁ и A₂ различаются сильнее всего, т. е. биоединиц, информативность которых наибольшая.

Для измерения количества информации Н. Винер и К. Шеннон независимо друг от друга в 1948 г. предложили логарифмические меры, получившие признание в качестве количественных мер информации. К классу подобных логарифмических мер относится введенная Jeffreus в 1946 г. и подробно изученная Кульбаком мера J расхождения между двумя статистическими распределениями [3, 4]:

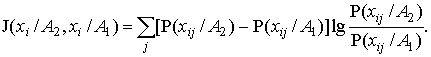(5)

Для использования в Неоднородной Последовательной Процедуре биопоказатели ранжируют по убывающей информативности, причем малоинформативные биоединицы в процедуре не участвуют.

Одним из ограничений применения НПП является возможное наличие нулевых вероятностей в диапазонах, на которые разбиваются выборки, поэтому существенным оказывается качество процесса разбивки на диапазоны [2, 3, 4].

Статистическая информация о 21 биопоказателе больных механической желтухой, оцененных экспертом, как наиболее значимые при принятии решения об операции, собрана из историй болезни в клинической больнице №5 г. Барнаула. Обработано 594 историй болезни для двух групп больных. Первая группа (состояние A₁) – 473 истории болезни, пациентов, которые выписаны из больницы после операции. Вторая группа (состояние A₂) – 121 история болезни больных умерших после операции. Биопоказатели больных фиксировались в десятидневный предоперационный период. Априорные вероятности состояний A₁ и A₂ составили 91 и 9 % соответственно.

Анализируя интегральные функции распределений вероятностей, и, используя алгоритм нахождения границ диапазонов, максимально сохраняющий различия распределений, мы добились максимальной информативности по каждому биопоказателю. Информативность вычислялась по формуле Кульбака, модифицированной Е.В. Гублером, для учета априорных вероятностей состояний [4]:

(6)

В процессе ранжирования биоедениц по убывающей информативности было исключено 3 малоинформативных биопоказателя.

Выделено 4 степени операционного риска, которым соответствуют следующие вероятности состояния A₂: I степень – от 60 до 70 %, II степень – от 70 до 80 %, III степень – от 80 до 90 % и IV степень – от 90 до 100 %.

Компьютерная реализация алгоритма НПП и формулы Байеса позволяет принять решение в пользу одного из двух рассматриваемых состояний при превышении одного из диагностических порогов. А если ни один из порогов не достигнут – оценить степень операционного риска у конкретного больного.

Результаты тестирования компьютерной программы на группе больных с состоянием A₂ представлены в следующей таблице:

Значения вероятности состояния A₂, % (степень риска)	Количество больных, %	Процент верификации состояния A₂ при α=1% и β=10%	Процент верификации состояния A₂ при α=5% и β=20%
от 0 до 50	30.6	–	–
от 50 до 60	6,7	–	–
от 60 до 70 ( I )	5.8	–	–
от 70 до 80 ( II )	1.6	–	–
от 80 до 90 ( III )	7.4	–	–
от 90 до 100 ( IV )	47.9	34.6	41.3

Как видно из таблицы, у 30.6 % больных вероятность состояния A₂ составила менее 50 %, т. е. в 30.6 % случаев мы получили ложный ответ. При вероятности состояния от 50 до 60 % (6.7 % случаев) ответ можно считать неопределенным, так как превышение вероятности состояния A₂ над вероятностью состояния A₁ не существенно.

В заключении хотелось бы отметить, что на достоверность ответов, полученных при тестировании, влияют не только количество биопоказателей и объемы выборок. Возможно, на послеоперационные состояния нескольких тестируемых больных повлияло оперативное вмешательство, которое в данной работе никак не учитывалось. По-видимому, стопроцентной или близкой к стопроцентной достоверности ответов при прогнозировании исхода операции по предоперационному состоянию больных ожидать не следует.

Литература

1. Боровков А. А. Теория вероятностей: Учеб. Пособие для вузов. – 2-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит. 1986. – 432 с.
2. Генкин А.А., Гублер Е. В. Применение непараметрических критериев статистики в медико – биологических исследованиях. - Л. : Медицина., 1973. – 141 с.
3. Гублер Е. В. Вычислительные методы анализа и распознавания патологических процессов. – Л. : Медицина., 1978. – 296 с.
4. Гублер Е. В. Информатика в патологии, клинической медицине и педиатрии. - Л. : Медицина., 1990. – 176 с.
5. Ластед Л. Введение в проблему принятия решений в медицине. – М. : Мир., 1971. – 315с.
6. Минцер О. П., Цуканов Ю. Т. Клиническое прогнозирование. – Киев : Здоров’я, 1983. – 144с.