Применение взаимного информационного критерия для выбора функции в автоматизированном диагнозе
Джорджия Д. Турэсси
Отделение Рентгенологии, Медицинский центр Университета Дьюка, Дарем, Северная Каролина 27710
Эрик Д. Фредерик
Объединение ЧимКодс, Дарем, Северная Каролина 27713
Миа К. Марки
Отделение Биомедицинской техники, Университет Дьюка, Дарем, Северная Каролина 27710
Кери Э. Флойд, младший.
Отделение Рентгенологии, Медицинский центр Университета Дьюка, Дарем, Северная Каролина 27710 и Отделение Биомедицинской техники, Университет Дьюка, Дарем, Северная Каролина 27710
(Получен 13 июня 2001; принятый для публикации 27 сентября 2001)
Цель данного исследования – изучение подхода теории информации к отбору признаков для
автоматизированного диагноза (САПР). Этот подход основан на концепции взаимной информации (ВИ).
ВИ измеряет общую зависимость случайных переменных, не делая предположения о природе их базовых
отношений. Следовательно, метод расчета информативности потенциально имеет некоторые преимущества
над методами отбора признаков, которые сосредотачиваются только на линейных зависимостях переменных.
Это исследование было основано на базе данных статистических функций текстуры, извлеченной из
отсканированных снимков перфузии легкого. Конечная цель – выбрать оптимальное подмножество функций
автоматизированного диагноза острой легочной эмболии (ЛЭ). Первоначально, исследование решало проблемы
относительно применения ВИ в ограниченном наборе данных, поскольку это часто имеет место в САПР.
Выбранные с помощью ВИ функции были сопоставлены с функциями, выбранными используя пошаговый линейный
дискриминантный анализ и генетические алгоритмы для той же самой базы данных ЛЭ. Линейные и нелинейные
модели выбора решения были реализованы с целью объединить выбранные функции в заключительный диагноз.
Результаты показали, что ВИ – эффективный критерий выбора функции для нелинейных моделей САПР,
преодолевающих некоторые из известных ограничений и вычислительные сложности других популярных методов
выбора функции в поле. ©2001 Американская Ассоциация Физиков в Медицине. [DOI: 10.1118/1.1418724]
Ключевые слова: взаимная информация, отбор признаков, компьютеризованный диагноз, острая легочная эмболия
I. ВВЕДЕНИЕ
Отбор признаков – процесс выбора подмножества функций, относящихся к конкретному приложению. Во время процесса отбора, критерий выбора используется для удаления несоответствующих или избыточных функций. Обширное исследование привело исследователей к оценке важности выбора функции при разработке к омпьютеризованных диагностических инструментов САПР. Оптимизированный отбор признаков уменьшает размерность данных и потенциально удаляет помехи, в результате инструменты САПР не только более точны, но также и более устойчивы. Несколько испытаний САПР показали положительное воздействие оптимизированного выбора функции [1–8].
Самый популярный алгоритм отбора признаков, используемых в САПР, является ступенчатый линейный дискриминантный анализ [9], заимствованный из линейной статистики. Он предназначен для уменьшения размерности характеристического вектора, выбирая ступенчатым способом функции, которые максимизируют линейную разделимость выходных классов. Интуитивно, метод отбора признаков, основанный на линейных предположениях, является не обязательно оптимальным подходом предварительной обработки данных, особенно когда сокращенный набор функций будет подаваться в нелинейные алгоритмы решения, такие как нейронные сети обратного распространения (ИНС-ОР). Следовательно, методы сокращения веса [10] и генетические алгоритмы [11] были предложены для отбора признаков с помощью ИНС-ОР как многообещающие варианты, лучше адаптированные в соответствии с нелинейной природой ИНС. Методы сокращения веса базируются на том, что функции, связанные с весом, близким к нулю могут быть устранены. С большими наборами данных подход сокращения веса может быть в вычислительном отношении дорогим, потому что сеть должна быть полностью обучена прежде, чем встретится любое сокращение. Более популярный и эффективный выбор для САПР – генетический алгоритм ГA. ГА – форма искусственного интеллекта, базирующаяся на биологических процессах развития. Основной подход состоит в создании совокупности в произвольном порядке выбранных сочетаний функций. Каждое сочетание считают возможным решением проблемы отбора признаков. Через теорию естественного отбора и генетической рекомбинации эти решения в будущем переходят в совокупности, где только диагностически важные сочетания функций остаются в живых. Основное преимущество ГA – способность исследовать множество возможных решений одновременно [11]. Не смотря на все преимущества, ГА в вычислительном отношении очень требовательны, особенно при увеличении количества доступных функций.
Целью данного исследования является изучение подхода теории информации к проблеме отбора признаков для приложений САПР. Этот подход использует понятие взаимной информации (ВИ) в качестве критерия выбора функции. По определению, ВИ является мерой информативности данного признака в условиях данной задачи [12]. Теоретически, критерий ВИ предлагает три основных преимущества перед другими методами [12]. Во-первых, ВИ измеряет общую статистическую зависимость между переменными, вопреки линейному коэффициенту корреляции. Во-вторых, ВИ является инвариантной к монотонным преобразованиям, выполняемых над переменными, вопреки линейным преобразователям данной размерности, таким как анализ главных компонентов. Наконец, подход выбора функции ВИ не зависит от алгоритма решения, таким образом, уменьшается вычислительная сложность по сравнению с ГА.
Понятие взаимной информации часто используется в обработке медицинских изображений, особенно для задач регистрации изображения. Тем не менее, применение ВИ в качестве критерия выбора функции использовалось достаточно редко. В 1994 Батити и др. представил применение ВИ для распознавания образов, используя моделируемые данные и калибровочные базы данных [20]. В 1996, Чжен и др. применили ВИ для отбора признаков, необходимых для распознавания образов, используя радиально-базисную нейронную сеть [21]. В недавнем времени вышеупомянутыми была представлена информационно-нечеткая нейронная сеть для отбора признаков [22]. В ходе изучения было оценено воздействие их метода отбора признаков на диагностическую производительность дерева решений.
Целью данной статьи является демонстрация применения и воздействия критерия ВИ для отбора признаков при обработке текстур на основе САПР для автоматизированной диагностической интерпретации медицинских изображений. Методы анализа текстур образуют набор функций с числовыми значениями, которые имеют различные по своей сути диагностические значения. Эти значения собираются в вектор функции характеристики текстур. Часто, характеристический вектор является предельно большим. Поэтому, сокращение функции является необходимым для оптимизации диагностической производительности и надежности результирующей САПР. Наше исследование основано на базе данных функций текстур, извлеченных из сканированных снимков перфузии легкого при постановке диагноза острой легочной эмболии. Конечная цель стоит в разработке САПР, которая использует наименьшее число функций текстур, не жертвуя диагностической производительностью. Учитывая базу данных изображений, мы стремимся применять и оценивать эффективность критерием ВИ, с целью совершенствования процесса выбора функции по сравнению с другими методами, широко использующимися в САПР.
II. МАТЕРИАЛЫ И МЕТОДЫ
A. Определение взаимного информационного понятия и его свойств
Взаимная информация (ВИ) – фундаментальное понятие в теории информации. Это показатель общей взаимозависимости между случайными величинами [12]. В частности, с учетом двух случайных величин X и Y, взаимная информация I(X; Y) определяется следующим образом:
 |
(1) |
H() – энтропия случайной величины и меры неопределенности, связанной с ней. Для непрерывной случайной переменной в состоянии X, H(X) определяется как
 |
(2) |
Если X является дискретной величиной, H(X) определяется следующим образом:
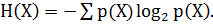 |
(3) |
В обоих случаях р(Х) представляет собой предельную вероятность распределения случайных величин X. На основании приведенных выше формул,
становится очевидным, почему энтропия часто считается мерой неопределенности. В качестве примера, пусть с.в. X представляет наличие болезни D.
Если нет неопределенности относительно наличия болезни  или отсутствие болезни
или отсутствие болезни 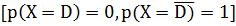 ,
то энтропия H(X) равна нулю. Однако, если существует высокая неопределенность относительно наличия или отсутствия заболеваний
,
то энтропия H(X) равна нулю. Однако, если существует высокая неопределенность относительно наличия или отсутствия заболеваний 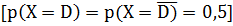 ,
то энтропия H(X) равна 1. Вообще, если любые из N болезней одинаково возможны
,
то энтропия H(X) равна 1. Вообще, если любые из N болезней одинаково возможны
 , то H(X) достигает своего максимального значения
, то H(X) достигает своего максимального значения  . Это значение представляет самую высокую неопределенность случайной величины X.
. Это значение представляет самую высокую неопределенность случайной величины X.
Используя правило Байеса о условных вероятностях, формулу (1) можно переписать в виде
 |
(4) |
Некоторые наблюдения могут быть сделаны на основании формулы (4). H(X) измеряется априорной неопределенностью случайной величины X. H(X|Y) измеряет
условную неопределенность X после того как наблюдается Y. Взаимная информация I(X; Y) измеряет, на сколько неопределенность X уменьшается, если Y не
наблюдается. Легко показать, что если X и Y, как правило, независимы, то H(X, Y) = H(X) + H(Y). Следовательно, их взаимная информация равна нулю, т. е.
наблюдения Y не уменьшает неопределенность X. Однако, если X = Y, то I(X; X) = H(X). Таким образом, энтропия – самостоятельная информация.
Так как взаимный обмен информацией не делает никаких предположений о характере отношений между переменными, это довольно общий характер и часто рассматривается как обобщенный коэффициент линейной корреляции. Однако, если X и Y являются гауссовские случайные величины, было показано, что их ВИ – простое преобразование их линейного коэффициента корреляции p [23]:
 |
(5) |
Понятие взаимной информации может быть легко расширено за счет включения более двух случайных величин. Согласно цепному правилу [12], объединим совместную
взаимную информацию (СВИ) между набором функций (Х1, Х2, Х3,…,XN) и результатом Y(т.е. диагнозом):
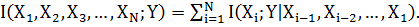 |
(6) |
СВИ была введена, чтобы описать, насколько информация, представленная вектором функций (Х1, Х2,…,XN)
снижает неопределенность в отношении с.в.Y. Учитывая большой набор функций, ожидается, что некоторые из них могут
быть зависимыми друг от друга. Таким образом, выбор функций на основе их индивидуальной ВИ может производить подмножества,
которые содержат информативно избыточные функции. СВИ является более подходящим критерием выбора функции, поскольку он может
обеспечить оптимальное подмножество, которое содержит не только самые подходящие, но и наименее избыточные функции.
B. Оценка взаимной информации
В этом разделе описываются методы, используемые в нашем исследовании для оценки взаимной информации между случайными величинами. ВИ между двумя случайными величинами X и Y (т. е. функция текстуры и диагностики ЛЭ) соответственно была оценена при помощи гистограммы. Согласно этому методу, функция плотности вероятности каждой переменной аппроксимируется с использованием гистограммы. Затем ВИ может быть рассчитана по следующей формуле:
 |
(7) |
где сумма рассчитывается по соответственно дискретизированным значениям случайных переменных X и Y [12].
Для каждого столбца гистограммы, объединенное распределение вероятности P(X, Y) оценивается путем подсчета количества случаев, которые попадают
в определенный интервал, и делят это число на общее количество случаев. Та же самая техника применяется для гистограммы аппроксимации предельных
распределений P(X) и P(Y).
Одним из важнейших вопросов является выбор количества интервалов. В прошлом некоторые исследователи использовали фиксированное количество интервалов,
выбранных эмпирически. Мы решили формализовать подход с использованием метода Гаусса, который применялся в обработке речи [24].
С негауссовых данных было
предложено  нужное количество интервалов для оценки гистограммы,
где
нужное количество интервалов для оценки гистограммы,
где  –
предполагаемый эксцесс [25]. При
–
предполагаемый эксцесс [25]. При  для гауссовских распределений,
нужное количество интервалов по правилу Стерджа составляет
для гауссовских распределений,
нужное количество интервалов по правилу Стерджа составляет
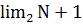 [25]. Кроме того, поскольку распределение значений
каждой функции не известны априори, диапазон значений делится на равные
отрезки. Для надежности, мы рассчитали среднее значение и стандартное отклонение каждого компонента. Затем, интервал
[25]. Кроме того, поскольку распределение значений
каждой функции не известны априори, диапазон значений делится на равные
отрезки. Для надежности, мы рассчитали среднее значение и стандартное отклонение каждого компонента. Затем, интервал
 был разделен на определенное количество равных частей. Любые случайные точки,
попадающие за пределы заданного
интервала, были присвоены крайним левым или правым интервалам при расчете гистограммы. Приведенные выше правила применяются последовательно для всех функций.
Очевидно, что случайная переменная, представляющая диагноз, дискретна по своей природе. Каждое возможное значение (0 или 1) представляет наличие или
отсутствие заболевания, соответственно.
был разделен на определенное количество равных частей. Любые случайные точки,
попадающие за пределы заданного
интервала, были присвоены крайним левым или правым интервалам при расчете гистограммы. Приведенные выше правила применяются последовательно для всех функций.
Очевидно, что случайная переменная, представляющая диагноз, дискретна по своей природе. Каждое возможное значение (0 или 1) представляет наличие или
отсутствие заболевания, соответственно.
Оценка СВИ между набором функций и диагнозом ЛЭ является более сложной. Учитывая набор, состоящий из N функций, есть 2N возможных подмножеств. При переборе требуется, чтобы СВИ была оценена для каждого из возможных подмножеств. Например, с 12 функциями, есть 4096 возможных подмножеств функции, которые должны быть рассмотрены. Подмножество функции, у которого есть максимальная СВИ с выходной переменной, является оптимальным. Число выбранных функций увеличивается по экспоненте, т.к. требуется больше выборок данных для достоверной оценки СВИ. Два эвристических подхода были предложены для выполнения этой задачи [20, 21]. Эти методы основаны на выборе функций в пошаговом режиме так, чтобы у каждой новой выбранной функции был самый высокий отдельный показатель ВИ и самый низкий показатель СВИ с заранее выбранной функции. Оба метода начинаются с выбора одной функции Xi, которая имеет самую высокую ВИ с выходной переменной Y. На каждом шаге выбора используется метод A, выбирая функцию кандидата Xj, который максимизирует взвешенное различие
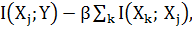 |
(8) |
где k представляет собой предварительно отобранные функции, а j – параметр функции кандидата [20]. Параметр принимает значения
от 0,5 до 1,0 и его оптимальное значение определяется эмпирически. Альтернативный метод B выполняется путем отбора функции кандидата Xj
с самым маленьким евклидовым расстоянием между точками максимума I(Xj; Y) и минимума 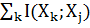 , где k – предварительно отобранные функции
[21]. Следует подчеркнуть, что оба метода неоптимальные и, как таковые, они не гарантируют бесперебойного предоставления лучшего
решения проблемы выбора функции.
, где k – предварительно отобранные функции
[21]. Следует подчеркнуть, что оба метода неоптимальные и, как таковые, они не гарантируют бесперебойного предоставления лучшего
решения проблемы выбора функции.
С. Применение в САПР
Методы ВИ на основе выбора функции были применены для автоматизированной диагностики острой легочной эмболии (ЛЭ). Приложение было основано на базе данных 45 пациентов, перенесших вентиляционно-перфузионную сцинтиграфию в связи с подозрением на острую ЛЭ. Ядерные исследования были выполнены и интерпретированы согласно протоколу PIOPED в Медицинском центре Университета Дьюка [26]. Сорок один из 45 сканирований были идентифицированы как недиагностирумые для ЛЭ, на основании исходных критериев PIOPED [27]. Следует отметить, что дифференциальный диагноз ЛЭ в выборке пациентов оказался достаточно сложной задачей. Большинству пациентов 84/90 связали дефекты перфузии со множеством заболеваний легких, часто сосуществующих с легочной эмболией то есть обструктивная болезнь легких, плевральный выпот, ателектаз, и паренхиматозные помутнения. В результате требовалась инвазивная легочная вазография, чтобы установить диагноз. Наличие ЛЭ было ангиографическим образом подтверждено у 13 пациентов и исключено у 32 пациентов. Кроме того, у 18 из 90 были идентифицированы дефекты, имеющие отношение к перфузии ЛЭ.
Та же самая база данных изображений была использована прежде для исследования фрактальных свойствах сканирований перфузии легкого [28]. Данное исследование направлено на анализ тех же изображений с использованием статистических характеристик текстур. Исследование сосредоточилось только на виде сзади сканирований перфузии легкого, анализируя в общей сложности 90 случаев в отдельности. Первоначально, естественный край нормального легкого был вручную обрисован в общих чертах опытным врачом ядерной медицины. Затем, анализ текстуры выполнялся на каждом обрисованном в общих чертах легком, с целью извлечения нескольких функций. Функции текстур были основаны на пространственной зависимости матрицы градации серого SGLD, которая описывает локальные взаимосвязи пар пикселей изображения с учетом их расстояния и угла направления [29, 30]. Изменяя расстояние и направление между парами пикселей, при определении пространственных отношений, могут быть построены различные SGLD. Для нашего исследования SGLD матрицы были сформированы для трех расстояний d 1,2,3 пикселей и четырех направлений 0°, 45°, 90°, 135°, общей сложности 12 SGLD матриц. Двенадцать параметров текстуры были рассчитаны от каждой матрицы SGLD взвешенным сочетанием матричных элементов. Текстура, параметры которой предложены Харалика, включают угловой момент инерции, контраст, корреляцию, дисперсию, обратный момент различия, среднее, суммарную дисперсию, суммарную энтропию, энтропию, энтропию различия и два информационных момента корреляции [29, 30]. Общее количество функций равнялось 144.
Было показано, что размерность вектора признаков увеличивается, что вносит смещение в разработку и оценку диагностических инструментов САПР [31, 32]. Эти смещения могут стать серьезной проблемой при ограничениях баз данных, как в нашем случае. Чтобы уменьшить потенциальное смещение, наше исследование сосредоточилось только на 12 функциях текстур. Специально, для каждой из 12 функций Харалика, то есть второй угловой момент, контраст, и т.д. мы сформировали среднее число через все интервалы и направления, которые рассматривались. Затем, мы сосредоточились на разработке инструментов САПР на основе только этих 12 «средних функций». САПР был разработан, так чтобы обнаружить ЛЭ в имеющихся сканированиях перфузии легкого. Таким образом, легкие каждого пациента были описаны с помощью 12 особенностей текстуры и рассмотрены как отдельный случай. Главной целью было разработать максимально производительную САПР, используя наименьшее возможное число доступных функций текстуры.
D. Оценка эффективности
На основе алгоритмов, описанных ранее, ВИ и СВИ были применены к набору данных ЛЭ, чтобы выбрать диагностически «информативные» функции текстур. Для сравнения мы также провели популярный ступенчатый выбор линейной функцией дискриминанта. Все методы выбора выполнялись на всем наборе данных прежде, чем было предпринято любое решения.
Т.о. пошаговый линейный дискриминантный анализ начинается с выбора функции с наибольшим различием в средних значениях между двумя классами. Различие измеряется путем дисперсионного анализа статистической величины F [9]. В последствии функция добавляется так, чтобы улучшалось различие модели функции кандидата в комбинации с уже существующими. Когда функция вводится в статистическую модель, рассматривают только ее линейную корреляцию с предварительно введенными результатами исследования. Кроме того, на любом шаге, никакое обнаружение не может быть удалено. Процесс выбора продолжается до тех пор, пока мощность модели улучшается. Конечным результатом поэтапного процесс выбора является подмножеством функций, упорядоченных по значимости. Концептуально, пошаговый выбор функции подобен методу приближения СВИ, описанному прежде. Они оба являются итерационными процессами и на каждом этапе они выбирают следующую важную особенность, основанную на уже выбранных. Различие заключается в измерении статистического отношения между функцией кандидата и предварительно введенными функциями.
Выбранные функции затем были объединены в окончательный диагноз с помощью линейных и нелинейных моделей решения. В качестве линейной модели был линейный дискриминантный анализ (ЛДА). Нелинейная модель представлена искусственной нейронной сетью (ИНС). Архитектура сети трехуровневая с прямой подачей, обученная с помощью метода Левенберга-Марквардта [33]. Этот метод был разработан для обучения сети прямой связью, значительно быстрее чем обычный алгоритм обратного распространения спада градиента. Количество входных узлов варьируется в зависимости от числа текстурных характерных для выбранных диагностических задач. Число скрытых узлов определялось эмпирически и было установлено, что достаточно четыре скрытых узла. Выходной слой имел один узел с целевыми значениями 0, если ЛЭ не было и 1, если ЛЭ присутствовала. Результаты были получены с помощью метода перекрестной проверки с исключением по одному образцу. Эксперименты ИНС выполнялись с использованием программного обеспечения MATLAB software The Math Works, Inc., Natick, MA. Пошаговый выбор функции и линейные модели выбора решения были реализованы с матобеспечением SAS/STAT software SAS Institute, Inc., Cary, NC, используя процессы STEPDISC и DISCRIM с опцией CROSSVALIDATE.
Анализ метода ВИ с пошаговыми линейными дискриминантными методами выбора функции был произведен, чтобы проверить гипотезу о преимуществе нелинейного метода выбора функции для нелинейной модели выбора решения. Кроме того, выбор функций с помощью ГА проводился в сочетании с моделью ИНС. Сравнение метода ВИ и ГА может продемонстрировать выгоды от применения метода с использованием ИНС.
Подход выбора функции с помощью ГA был описан прежде [3, 6, 7]. Как правило, он начинается с большого числа комбинаций функций, каждая из которых пытается оптимизировать производительность САПР в данной базе данных. Совокупность называют поколением. Каждая комбинация функций называется хромосомой и представляет собой различные решения проблемы выбора функции. Хромосомы копируются для формирования новой популяции хромосом в зависимости от их целевой функции. Фитнесс-функция измеряет «качество» хромосом. Для этого приложения адекватная фитнесс-функция – операционная характеристика приёмника (ROC), полученная ИНС, использующей определенное сочетание функций, представленных хромосомами. Чем индекс ROC ИНС, тем больше вероятность того, что хромосома выживет и будет способствовать следующему поколению. Следовательно, ожидаемый относительный процент встречаемости хромосомы в новой поколении – член пропорции своей фитнесс-функции, то есть отбор колеса рулетки [11]. Размноженные хромосомы переносят «перекрестное соединение» таким образом, чтобы компоненты от лучших хромосом могли быть объединены. Мутация может происходить путем случайного изменения случайно выбранных генов. Вышеупомянутая последовательность отбора, перекрестного соединения, и мутации продолжается, пока не появится лучшее сочетание функций. Применение функции выбора с помощью ГA очень трудоемкое, поскольку требует обучения и тестирования нескольких ИНС для многих поколений. На языке программирования C были написаны пользовательские программы, используемые для реализации алгоритма ГA. Программа работала на UltraSPARC workstation (Sun Microsystems, Mountain View, CA). Поиск ГА был осуществлен в течение 50 поколений. Каждое поколение содержит 100 хромосом. Кроссоверная ставка была установлена на уровне 50%, а частота мутаций была установлена на уровне 0,1%. Для каждой хромосомы была реализована ИНС и оценки использования метода перекрестной проверки с исключением по одному образцу.
| Парамтр | Асимметрия | эксцесс |
|---|---|---|
| F1: Второй угловой момент | 2,05 | 0,48 |
| F2: Контрастность | -2,40 | 2,73 |
| F3: Корреляция | -5,19 | 3,77 |
| F4: Отклонение | -0,12 | -0,51 |
| F5: Разница обратных моментов | 2,71 | 1,06 |
| F6: Сумма средних | -1.00 | 0,09 |
| F7: Сумма отклонений | 0,03 | -0,55 |
| F8: Сумма энтропии | -2,71 | 0,98 |
| F9: Энтропия | -2,91 | 0,98 |
| F10: Разница энтропии | -3,41 | 1,45 |
| F11: Информационная мера корреляции | -0,06 | 1,52 |
| F12: Информационная мера корреляции | -3,87 | 2,61 |
Диагностическая производительность измерялась на основе показателей ROC области. Мы использовали пакет программного обеспечения ROCKIT, разработанный Мецом и др. в Чикагском университете (http:// www-radiology.uchicago.edu/krl/toppage11.htm), в итоге ROC изгибы соответствовали выходным реакциям моделей выбора решения, реализованных в данном исследовании.
III. РЕЗУЛЬТАТЫ
A. Негауссовость параметров текстуры
Для определения количества интервалов, необходимых для оценки гистограммы ВИ и СВИ, сначала проверяли, действительно ли распределение
каждой функции является гауссовым. Несколько методов были предложены для тестирования гауссовости набора данных. Для данного исследования мы
проверили нормированную асимметрию и нормированный эксцесс [34]. Нулевой гипотизой для вышеуказанных тестов является то, что ряд наблюдений
следует распределению Гаусса, если нормированная асимметрия и нормированный эксцесс данных подчиняются стандартному гауссовскому распределению N(0,1).
Нормированная асимметрия и нормированный эксцесс определяются следующим образом:
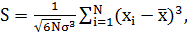 |
(9) |
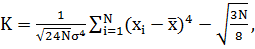 |
(10) |
где N, X, является размер выборки, выборочное среднее и отклонение образца стандарта. На уровне значимости 0,05, критическое значение для стандартного распределения Гаусса являются 1,96. Таблица I, содержит нормированную асимметрию и эксцесс для каждой из 12 текстурных особенностей нашего набора данных. В таблице можно заметить некоторые особенности отображения негауссовых свойств, а именно абсолютную величину или нормированную асимметрию, нормированный эксцесс или оба параметра, превышающие критическое значение 1,96. В зависимости от того, используется функция Гаусса или нет, мы следуя формулам, приведенным в главе II B, рассчитали оптимальное количество интервалов. Для наших данных, количество интервалов составляет от 5 до 10. Так как, наш набор данных состоит из смеси гауссовых и негауссовых, в изучение взаимного критерий информации как метод выбора функций оправдано. Если есть диагностически важные отношений между негауссовыми особенностями, то с помощью ВИ потенциально можно определить их как более эффективные по сравнению с коэффициентом линейной корреляции.
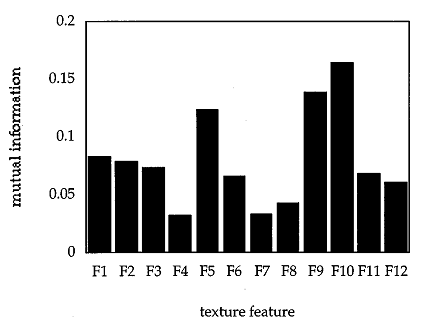
Рис. 1. Взаимная информация между каждым параметром текстуры и диагнозом.
B. ВИ между функцией и диагнозом
Рис. 1 показывает взаимную информацию между каждой функцией и диагнозом. Оценка производится на основе всех имеющихся случаев набора данных. Очевидно, что функции F10, F9 и F5 выделяется как наиболее «информативные» для диагностики ЛЭ. Это довольно интересно, так как отдельное исследование ROC показывает, что функции F2 и F11 являются самыми прогнозирующими для ЛЭ с независимыми указателями области ROC АZ(F2)=0.73±0.06 и АZ(F11)=0.70±0.06, соответственно. Оставшиеся функции показали отдельные области ROC близкие к случайному свойству, располагающемуся между 0.51 и 0.60 (Рис. 2).
С. Воздействие метода отбора признаков на производительность САПР
В таблице II приведены результаты исследования. Таблица отображает подмножества функций, выбранных, используя метод пошагового линейного дискриминанта и ВИ. Для каждого подмножества таблица показывает область ROC индексации, полученных с помощью моделей линейных решений (ЛР) и нелинейных ИНС, используемые для объединения того же самого подмножество функций в конечный диагноз. В таблице приведены результаты для шести выбранных функций. При этом, диагностическая производительность обеих моделей выбора решения увеличилась больше чем шесть раз.
Все 12 функций, входящих как в ЛР, так и в ИНС, имеют клинически неприемлемый диагноз, хотя ИНС (AZ=0,64±0,07) очевидно лучше, чем ЛР (AZ=0,53 ± 0,07). Однако разница не была статистически значимой, в первую очередь в связи с небольшим числом случаев.
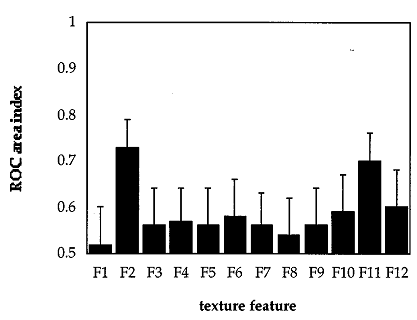
Рис. 2. Независимая область ROC индексации с соответствующим значением погрешности для каждой функции текстуры.
Очевидно, что выбранные с помощью ВИ и СВИ функции отличаются от выбранных с помощью ступенчатого линейного метода. Различные методы выбора решения повлияли на диагностическую эффективность модели. Лучшая линейная модель выбора решения достигает ROC-индекса в пределах 0,70±0,06. Для первых двух функций F2, F12 выбран ступенчатый линейный метод. По сравнению с ИНС достигнута значительно лучшая диагностическая производительность.(AZ=0,82±0,06). ИНС использовали пять функций (F10, F9, F5, F1, F2), выбранных самостоятельно исходя из значения ВИ для постановки конечного диагноза.
Стоит отметить, что хотя отбор признаков был оптимизирован, используя линейный метод, нелинейная модель выбора решения (ИНС) оказалась неспособна улучшить диагностическую производительность линейной модели выбора решения (ЛР). Тем не менее, ИНС выиграла за счет диагностических возможностей компонентов, выбранных с помощью ВИ, в то время как ЛР показала неутешительные результаты с любым из ВИ или СВИ.
Метод выбора функций, основанный на СВИ, работала лучше с ИНС, чем ЛР. Однако, никакой из двух методов приближенных вычислений СВИ, реализованных в ходе изучения, не смог достигнуть лучшей диагностической производительности, чем независимо выбранные основанные на ВИ функции. Хотя различия не были статистически значительны.
Дальнейший отбор с помощью ГА был вычислительно очень требовательный. Как упоминалось ранее, поиск ГА был осуществлен в течение 50 поколений. Примерно через пять поколений, некоторые комбинации функций начали проявляться, как диагностически более успешные. В частности F1, F2, F5 и остались наиболее успешными хромосомами до конца. ГА отобрал функции множества {F1, F2, F5, F10}, как оптимальные в конце тридцать восьмого поколения. Эти функции немного отличаются от выбранных с помощью подхода ВИ {F1, F2, F5, F9, F10}. На самом деле функции множества {F1, F2, F5, F9, F10} была выявлены ГА через шесть поколений. Поиск с помощью ГА продолжается, пока не будет удалена функция F9. Полная область ROC индексации, достигнутая ИНС, является тем же самым использованием любого подмножества, избавляющегося от избыточности (F9), как при подходе, базируемом на ВИ.
| Отобранный параметр | ЛР | ИНС |
|---|---|---|
| Все | 0.53±0.07 | 0,64±0,07 |
| Пошаговый метод | ||
| F2, F12 | 0,70 ± 0,06 | 0,68 ± 0,07 |
| F2, F12, F4 | 0,69 ± 0.07 | 0,68 ± 0,06 |
| F2, F12, F4, F11 | 0,70 ± 0,06 | 0,67 ± 0,07 |
| F2, F12, F4, F11, F5 | 0,69 ± 0,06 | 0,69 ± 0,07 |
| F2, F12, F4, F11, F5, F7 | 0,67 ± 0,07 | 0,65 ± 0,09 |
| ВИ | ||
| F10, F9 | 0,58 ± 0,07 | 0,73 ± 0,07 |
| F10, F9, F5 | 0.61 ± 0.07 | 0,72 ± 0,05 |
| F10, F9, F5, F1 | 0,59 ± 0,07 | 0,70 ± 0,08 |
| F10, F9, F5, F1, F2 | 0,60 ± 0,07 | 0,82 ± 0,06 |
| F10, F9, F5, F1, F2, F3 | 0,60 ± 0,07 | 0,75 ± 0,07 |
| СВИ-A (β = 0.5) | ||
| F10, F9 | 0,58 ± 0,07 | 0,73 ± 0,07 |
| F10, F9, F3 | 0,55 ± 0,07 | 0,67 ± 0,07 |
| F10, F9, F3, F2 | 0,64 ± 0,07 | 0,74 ± 0,08 |
| F10, F9, F3, F2, F1 | 0,62 ± 0,07 | 0,78 ± 0,07 |
| F10, F9, F3, F2, F1, F4 | 0,61 ± 0,07 | 0,73 ± 0,07 |
| СВИ-B (Евклидов) | ||
| F10, F3 | 0,51 ± 0,08 | 0,64 ± 0,07 |
| F10, F3, F1 | 0,64 ± 0,07 | 0,66 ± 0,07 |
| F10, F3, F1, F2 | 0,63 ± 0,07 | 0,79 ± 0,08 |
| F10, F3, F1, F2, F4 | 0,61 ± 0,07 | 0,76 ± 0,06 |
| F10, F3, F1, F2, F4, F11 | 0,67 ± 0,07 | 0,69 ± 0,07 |
D. Результат применения метода приближенных вычислений ВИ для отбора признаков
Число диапазонов, выбранных для гистограммы аппроксимации распределений вероятностей, соответствующих расчетам ВИ, является важным вопросом. Большее количество диапазонов позволяет получить более детальное представление о вероятностных распределений, что видно из формулы (7). Тем не менее, эти данные могут быть не более чем шум, вызванный небольшим размером выборки в каждом диапазоне. Потенциальная погрешность оценки может кардинально изменить результаты исследования. Небольшое количество положительных случаев нашего набора данных вызывает беспокойство.
Как упоминалось ранее, часто на практике определения количества диапазонов производится эмпирически, путем пробы несколько различных значений,
которые остаются фиксированными для всех функций. Мы изучили этот подход. В частности мы провели оценки ВИ, установив в качестве количества
диапазонов фиксированное значение (3, 5, 8 и 10) для всех функций. Нижние и верхние значения были выбраны следующим образом. Если предположить,
что все функции соответствуют функциям Гаусса, то в соответствии с формулой Стерджесса количество ячеек – 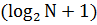 . Так как количество
положительных случав (N=18) меньше чем отрицательных (N=72), консервативная оценка — пять диапазонов
. Так как количество
положительных случав (N=18) меньше чем отрицательных (N=72), консервативная оценка — пять диапазонов  . В крайнем случае,
используются только три диапазона. Десять диапазонов были отобраны в качестве верхнего предела, которое подтверждается результатами в разделе III А.
. В крайнем случае,
используются только три диапазона. Десять диапазонов были отобраны в качестве верхнего предела, которое подтверждается результатами в разделе III А.
| Три диапазона | Пять диапазонов | Переменное число диапазонов | |
|---|---|---|---|
| ВИ | F2, F11, F9, F10, F5, F3 | F10, F5, F2, F11, F1, F9 | F10, F9, F5, F1, F2, F3 |
| СВИ-А | F2, F10, F5, F9, F8, F1 | F10, F3, F2, F12, F11, F4 | F10, F9, F3, F2, F1, F4 |
| СВИ-B | F2, F11, F12, F1, F3, F4 | F10, F5, F9, F8, F1, F2 | F10, F3, F1, F2, F4, F11 |
Ниже приведены подмножеств SN особенностей с учетом их «информационного содержания», где N – фиксированное количество диапазонов,
используемых для аппроксимации гистограммы:
S5={F10, F5, F2, F11, F1, F9, F4, F6, F7, F12, F8, F3},
S8={F10, F5, F2, F11, F6, F9, F12, F7, F4, F8, F1, F3},
S10={F10, F5, F11, F4, F8, F9, F1, F7, F2, F3, F6, F12}.
Общий порядок функций значительно зависит от количества использованных диапазонов для аппроксимации гистограммы. Некоторые текстуры последовательно преобладали, как более важные (F2, F5, F9, F10). Интересно, что используя три диапазона, две функции с самой высокой ВИ (F2 и F11) оказались те, которые имеют независимый друг от друга наибольший индекс ROC. Этот результат свидетельствует о том, что очень маленькое количество диапазонов может быть более подходящим для конкретно этой базы данных. Результаты использования двух методов СВИ для производства подмножеств функций, с помощью трех и пяти диапазонов представлены в таблице III. Хотя метод СВИ, основанный на трех диапазонах и метод СВИ, основанный на пяти диапазонах, показали хороший результат, выбранное подмножество функций, которые достигли указателей области ROC, с помощью ИНС, дали результат выше, чем лучший, что видно из Таблицы II. Оба метода, однако, подтверждают, что сочетание функций {F1, F2, F5, F9, F10} является диагностически важным.
IV. ОБСУЖДЕНИЕ
По определению, САПР может рассматриваться как система, которая уменьшает неопределенность в медицинской диагностике с помощью информации, заложенной в компоненты вектора. Многие САПР базируются на сложных схемах обработки изображений, которые производят векторы признаков с большой размерностью. На практике добавление новых функций в САПР часто может ухудшить его диагностичскую производительность. Этот эффект хорошо известен в распознавании образов под названием «проклятие размерности» [10]. Следовательно, оптимизация выбора характеристик в любой схеме САПР имеет решающее значение.
Основным направлением этой работы является изучение концепции взаимной информации в качестве критерия выбора функции в САПР. В первую очередь это сравнительное исследование рассчитано на небольшую базу данных клинически сложных сканирования перфузии легких. Исследование показало, что концепция ВИ предоставляет некоторые возможности, не доступные при использовании функций выбора методов, традиционно используемых в САПР. Некоторые из них рассмотрены ниже.
Взаимная информация является мерой информативности. Таким образом, она может использоваться для измерения информационного содержания компонента или набор функций и желаемого результата (то есть, правильного диагноза). Отдельные компоненты или подмножества компонентов с низким информационным содержанием могут быть исключен из САПР. Использование критерия для ликвидации избыточных функций далеко не уникальный подход. Отбор с помощью пошагового линейного дискриминанта основан на той же идеи. Однако критерий отбора ВИ имеет преимущества потому, что он измеряет не только линейные, но и общие зависимости. Если между имеющимися функциями существуют нелинейные зависимости, и они диагностически значимы, то ВИ лучше подходит для решения нелинейных моделей, таких как популярный ИНС. Наше исследование подтвердило это. Когда отбор признаков был «оптимизирован», используя линейный метод, линейная (ЛР) и нелинейная модели решения (ИНС) достигли той же производительности. Когда функции были отобраны исходя из более общей концепции ВИ, ИНС достиг значительно лучшей диагностической производительности, чем ЛР. Следует отметить, что для функций подмножества, которые оказались наиболее диагностически важными для ИНС характерны негауссовые особенностей.
Генетические алгоритмы были введены в САПР для решения именно этой проблемы. Не смотря на эффективность, они вычислительно очень требовательны, потому как выбор функций и решения моделирования выполняются ГА одновременно. При увеличении числа функций, ГА становится нецелесообразным, реализуя сложный алгоритм решения и сложные схемы выборки данных. В нашем исследовании подход с использованием ГА был вычислительно очень требователен, в первую очередь это касается схемы выборки. Наши исследования показали, что метод отбора на основе ВИ является конкурентной альтернативой. Учитывая нашу базу данных, выбранные с помощью ВИ подмножества функций были похожи на тех, которые определены ГА как диагностичски значимые. Так как основанный на ВИ отбор признаков выполняется прежде, чем выполняется моделирование решения, в вычислительном отношении метод доступен для баз данных, которые содержат сотни функций текстуры. Прежде показано [35], что при увеличении диапазонов, метод приближенных вычислений гистограммы имеет тенденцию переоценивать ВИ вследствие размерного эффекта конечных данных. Авторы выдвинули гипотезу, что этот результат переоценки не должен влиять на относительное упорядочивание функций [20, 21]. Однако это верно, только если данные раздела отражают базовое распределение вероятностей для каждой функции. Что является безусловно важным вопросом для нашего набора данных, учитывая небольшое количество позитивных случаев. Упорядочение функций существенно меняется в зависимости от количества диапазонов, использованных для оценки ВИ и СВИ. Хотя общий порядок функций изменятся в зависимости от того, сколько диапазонов использовалось для аппроксимации гистограммы, некоторые текстуры, все же, преобладали как наиболее важные (F5, F9, F1, F2, F10). Как определить число, и размер каждого диапазона – является постоянной темой для исследования в теории информации. Для решения данной задачи были предложены сложные адаптивные методы дискретности [36–38]. На практике мы обнаружили, что количество диапазонов зависит от гауссовости или негауссовости данных. Тем не менее, выбор фиксированного числа столбцов гистограммы очень консервативный, исходя из того, что три и пять диапазонов дали очень похожие результаты.
На первый взгляд, это удивительно, что метод СВИ смог повысить производительность САПР, достигнутую на основе ВИ объектов (таблица II). Такой результат подразумевает, что была избыточность среди диагностически важных функций. Что является не верным, исходя из того, что ГА смог определил одну функцию F9. Однако, учитывая небольшое количество действительно положительные случаев, ожидается, что оценка ВИ между любыми двумя функциями текстуры будет очень предвзятой, влияя на полное ступенчатое упорядочивание выбранных функций. Небольшой набор данных может вызвать значительные колебания в оценке ВИ, так как многие диапазоны гистограммы остаются «незанятыми». Эти колебания увеличивают предполагаемую ВИ, потому что они интерпретируются как важные структурные данные объединенного распределения вероятности. Переоценка ВИ между двумя функциями текстуры означает переоценку уровней их избыточности, которые могут влиять в основном на результаты отбора признаков с помощью СВИ.
Другая важная проблема, возникающая при отборе признаков в ограниченных наборах данных – смещение, получаемое, когда тот же самый набор данных используется для разработки классификатора и отбора признаков [31, 39]. Оба метод, ступенчатый линейный и основанный на ВИ метод отбора признаков были реализованы, используя целый набор данных, полученных в ходе нашего исследования. Поэтому, производительность САПР, возможно, была завышена в обоих случаях. Однако, вследствие сравнительного характера нашего изучения, это потенциальное смещение в результате должно иметь ограниченный эффект. Теоретически, такой подход при ГА не застрахован от смещения, т.к. выбор функций и решения моделирования выполняются одновременно.
И наконец, моделью САПР, которая работает лучше всего при диагностики ЛЭ является ИНС, которая использует четыре текстурных особенности: второй угловой момент (F1), контрастность (F2), обратный момент разностей (F5) и разницу энтропии (F10). Полная диагностическая производительность ИНС в диапазоне 0,82 ±0,06 основана на наборе клинически сложных сканирования перфузии легких. Производительность ИНС сопоставима с опытом врача ядерной медицины (AZ=0,81 ± 0,08) и ИНС, которая использует мультифрактальную текстурную информацию (AZ=0,81 ± 0,06) [28]. Нужно отметить однако, что диагностическая производительность врача была основана на полном наборе сканированных изображений перфузии, сканировании дыхательных путей, рентгенограммы грудной клетки, а не только на сканировании перфузии легкого. Итак, наше исследование показало, что взаимная информация является перспективным критерием при выборе функции для нелинейных моделей САПР. Объединяется вычислительная простота ступенчатых линейных методов отбора с эффективностью генетических алгоритмов. Особое внимание должно быть уделено оценке ВИ из ограниченного набора данных.
ПОДТВЕРЖДЕНИЕ
Эта работа была поддержана грантом № 98-0324 от Фонда Уитакер.
a)Electronic mail: gt@deckard.mc.duke.edu
- J.Y. Lo, J.A. Baker, P.J. Kornguth, and C.E. Floyd, Jr., "Computeraided diagnosis of breast cancer: artificial neural network approach for optimized merging of mammographic features", Acad. Radiol. 2, 841–850 1995.
- M.F. McNitt-Gray, H-K. Huang, and J.W. Sayre, "Feature-selection in the pattern classification problem of digital chest radiograph segmentation", IEEE Trans. Med. Imaging 14, 537–547 1995.
- B. Sahiner, H-P. Chan, D.T. Wei, N. Petrick, M.A. Helvie, and M.M. Goodsitt, "Image feature selection by a genetic algorithm: Application to classification of mass and normal breast tissue", Med. Phys. 23, 1671–1684 1996.
- G.D. Tourassi, C.E. Floyd, Jr., and R.E. Coleman, "Improved noninvasive diagnosis of acute pulmonary embolism using optimally selected clinical and chest radiographic findings" Acad. Radiol. 3, 1012–1918 1996.
- H-P. Chan, B. Sahiner, K.L. Lam, N. Petrick, M.A. Helvie, M.M. Goodsitt, and D.D. Adler, "Computerized analysis of mammographic microcalcifications in morphological and texture feature spaces", Med. Phys. 25, 2007–2019 1998.
- B. Sahiner, H-P. Chan, N. Petrick, M.A. Helvie, and M.M. Goodsitt, "Design of a high-sensitivity classifier based on a genetic algorithm: application to computeraided diagnosis", Phys. Med. Biol. 43, 2853–2871 1998.
- B. Zheng, Y-H. Chang, X-H. Wang, W.F. Good, and D. Gur, "Feature selection for computerized mass detection in digitized mammograms by using a genetic algorithm", Acad. Radiol. 6, 327–332 1999.
- M.F. McNitt-Gray, E.M. Har, N. Wyckoff, J.W. Sayre, J.G. Goldin, and D.R. Aberle, "A pattern classification approach to characterizing solitary pulmonary nodules imaged on high resolution CT: Preliminary results", Med. Phys. 26, 880–888 1999.
- R.J. Jennrich, "Stepwise discriminant analysis", in Statistical Methods for Digital Computers, edited by K. Einslein, K. Ralston, and H.S. Wilf Wiley, New York, 1977.
- C.M. Bishop, Neural Networks for Pattern Recognition Clarendon, Oxford, 1995.
- D.E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning Addison-Wesley, Reading, MA, 1989.
- T.M. Cover and J.A. Thomas, Elements of Information Theory Wiley, New York, 1991 .
- C. Studholme, D.L.G. Hill, and D.J. Hawkes, "Automated threedimensional registration of magnetic resonance and positron emission tomography brain images by multiresolution optimization of voxel similarity measures", Med. Phys. 24, 25–35 1997.
- S. Sanjay-Gopal et al., "A regional registration technique for automated interval change analysis of breast lesions on mammograms", Med. Phys. 26, 2669–2679 1999.
- J.P.W. Pluim, J.B.A. Maintz, and M.A. Viergever, "Image registration by maximization of combined mutual information and gradient information", IEEE Trans. Med. Imaging 19, 809–814 2000.
- L. Thurfjell et al., "Improved efficiency for MRI-SPET registration based on mutual information", Eur. J. Nucl. Med. 27, 847–856 2000.
- J.F. Krucker, C.R. Meyer, G.L. LeCarpentier, J.B. Fowlkes, and P.L. Carson, "3D spatial compounding of ultrasound images using image-based nonrigid registration", Ultrasound Med. Biol. 26, 1475–1488 2000.
- G. Berks, A. Ghassemi, and D.G. von Keyserlingk, "Spatial registration of digital brain atlases based on fuzzy set theory", Comput. Med. Imaging Graph. 25, 1–10 2001.
- M.A. Viergever, J.B.A. Maintz, W.J. Niessen, H.J. Noordmans, J.P.W. Pluim, R. Stokking, and K.L. Vincken, "Registration, segmentation, and visualization of multimodal brain images", Comput. Med. Imaging Graph. 25, 147–151 2001.
- R. Battiti, "Using mutual information for selecting features in supervised neural net learning", IEEE Trans. Neural Netw. 5, 537–550 1994.
- G.L. Zheng and S.A. Billings, "Radial basis function network configuration using mutual information and the orthogonal least squares algorithm", Neural Networks 9, 1619–1637 1998.
- M. Last, A. Kandel, and O. Maimon, "Information-theoretic algorithm for feature selection", Pattern Recogn. Lett. 22, 799–811 2001.
- W. Li, "Mutual information functions versus correlation functions", J. Stat. Phys. 60, 823–837 1990.
- H.H. Yang, S. Van Vuuren, S. Sharma, and H. Hermansky, "Relevance of time frequency features for phonetic and speaker-channel classification", Speech Commun. 31, 35–50 2000.
- W.N. Venables and B.D. Ripley, Modern Applied Statistics with S-Plus Springer, New York, 1994.
- A. Gottschalk, J.E. Juni, H.D. Sostman, R.E. Coleman, J. Thrall, K.A. McKusick, J.W. Froelich, and A. Alavi, "Ventilation-perfusion scintigraphy in the PIOPED study: Part I. Data collection and tabulation", J. Nucl. Med. 34, 1109–1118 1993.
- The PIOPED Investigators, "Value of the ventilation/perfusion scan in acute pulmonary embolism: Results of the prospective investigation of pulmonary embolism diagnosis PIOPED", J. Am. Med. Assoc. 263, 753–2759 1990.
- G.D. Tourassi, E.D. Frederick, C.E. Floyd, Jr., and R.E. Coleman, "Multifractal texture analysis of perfusion lung scans as a computer aid for acute pulmonary embolism", Comput. Biol. Med. 31, 15–25 2001.
- R.M. Haralick, K. Shanmugan, and I. Dinstein, "Textural features for image classification", IEEE Trans. Syst. Man Cybern. 3, 610–621 1973.
- R.M. Haralick, "Statistical and structural approaches to texture", Proc. IEEE 67, 786–804 1979.
- H-P. Chan, B. Sahiner, R.F. Wagner, and N. Petrick, "Classifier design for computeraided diagnosis: Effects of finite sample size on the mean performance of classical and neural network classifiers", Med. Phys. 26, 2654–2668 1999.
- B. Sahiner, H-P. Chan, N. Petrick, R.F. Wagner, and L. Hadjiiski, "Feature selection and classifier performance in computeraided diagnosis: The effect of finite sample size", Med. Phys. 27, 1509–1522 2000.
- M.T. Hagan and M. Menhaj, "Training feed-forward networks with the Marquardt algorithm", IEEE Trans. Neural Netw. 5, 989–993 1994.
- A. Stuart and J.K. Ord, Kendall's Advanced Theory of Statistics Edward Arnold, Paris, 1994 , Vol. 1.
- A. Treves and S. Panzeri, "The upward bias in measures of information derived from limited data samples", Neural Comput. 7, 399–407 1995.
- A.M. Fraser and H.L. Swinney, "Independent coordinates for strange attractors from mutual information", Phys. Rev. A 33, 1134–1140 1986.
- G.A. Darbellay and I. Vajda, "Estimation of the information by an adaptive partitioning of the observation space", IEEE Trans. Inf. Theory 45, 1315–1321 1999.
- G.A. Darbellay, "An estimator of the mutual information based on a criterion for independence", Comput. Stat. Data Anal. 32, 1–17 1999.
- M.A. Kupinski and M.L. Giger, "Feature selection with limited datasets", Med. Phys. 26, 2176–2182 1999.