Кластеризация и непрерывный алгоритм К-средних
Венс Фабер
Перевод:
Дрындик Р.В.
Источник (англ): http://citeseerx.ist.psu.edu
Многие виды анализа данных, такие как интерпретация изображений Landsat обсуждающиеся в сопроводительной статье, включают настолько большие наборы данных, что их непосредственное использование нецелесообразно. Сначала должны быть применены некоторые методы сжатия или консолидации, чтобы уменьшить размер входного набора информации без потери основных характеристик. Все методы консолидации теряют некоторые детали. Самая лучшая информация пригодная, по крайней мере, для практического применения, содержатся в исходных данных. Здесь мы представляем несколько широко используемых алгоритмов, уплотняющих данные посредством кластеризации, или группировки. Затем, мы представим новый алгоритм непрерывных К-средних. Данный алгоритм разработан в лаборатории специально для кластеризации больших наборов данных.
Кластеризация предполагает деление набора точек данных на непересекающиеся группы, или кластеры, в пределах которых точки «больше похожи» друг на друга, чем на точки в других кластерах. Термин «больше похож», применительно к кластерным точкам, как правило, означает близость. Когда набор данных кластеризован, каждая точка включается в определенный кластер и может быть охарактеризована одной описательной точкой, как правило, средней точкой в кластере. Любое конкретное разделение всех точек данных в кластеры называется разбиением.
Одним из наиболее известных приложений кластеризации является классификация растений или животных в отдельные группы или виды. Тем не менее, основная цель кластеризации данных – уменьшение размера и сложности данных. Сокращение данных осуществляется заменой координаты каждой точки в кластере координатами описательной точки кластера. Кластеризованные данные требуют значительно меньше ресурсов памяти и ими можно манипулировать гораздо быстрее, чем исходными данными. Значение того или иного метода кластеризации будет зависеть от того, насколько точно точки представляют собой данные, а также, насколько быстро работает программа.
Типичным примером кластера является деление результатов студенческих тестов на пять групп, обозначенных буквами A, B, C, D и F (Рисунок 1). Оценки выражены в процентах. Результатами тестов являются данные точки, и каждый кластер является средним результатом тестов. Буквенные оценки можно рассматривать, как символ замены численных значений. Результаты тестов являются примером одномерных данных, каждая точка данных представляет собой одну измеряемую величину. Многомерные данные могут включать в себя любое количество измеряемых атрибутов. Биолог, например, может использовать четыре признака характеристик уток (четырехмерные данные: размер, прямолинейность, толщину и цвет) для деления большого набора уток на несколько видов. Каждая независимая характеристика или измерение является одним измерением. Для консолидации больших датасетов главным является полем является кластерный анализ. Ниже мы опишем несколько методов кластеризации. Во всех этих методах необходимое количество кластеров k задано заранее. Описательная точка 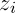 для кластера
для кластера 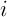 , как правило, является центром тяжести кластера. В случае одномерных данных, таких как результаты тестов, центр тяжести – это среднее арифметическое значений точек в кластере. Для многомерных данных, где каждая точка имеет несколько измерений, центр тяжести будет иметь одинаковое число компонент и каждая компонента будет средним арифметическим соответствующих составляющих точек кластера.
, как правило, является центром тяжести кластера. В случае одномерных данных, таких как результаты тестов, центр тяжести – это среднее арифметическое значений точек в кластере. Для многомерных данных, где каждая точка имеет несколько измерений, центр тяжести будет иметь одинаковое число компонент и каждая компонента будет средним арифметическим соответствующих составляющих точек кластера.
Рис 1. Кластеризация результата тестов
Возможно, самым простым и самым старым автоматизированным методом кластеризации является объединение точек в кластеры попарно. Все точки сгруппированы в необходимое количество кластеров. Такой агломеративный алгоритм можно найти во многих статистических пакетах. На рисунке 2 показан метод, применяемый для набора тестов, показанных на рисунке 1. Есть два основных недостатка этого алгоритма. Первый – он абсолютно неэффективен для анализа больших объемов данных. Каждый этап процедуры требует вычисления расстояния между всевозможными парами точек данных и сравнения всех расстояний. Второй связан с более фундаментальной проблемой кластерного анализа: несмотря на то, что алгоритм всегда дает нужное количество кластеров, центр тяжести этих кластеров не может представлять данные.
Что определяет «хорошую» или представительную кластеризацию? Рассмотрим один кластер со своим центром. Если точки тесно сгущены вокруг центра тяжести, то он может характеризовать каждого представителя этого кластера. Стандартная мера рассеяния группы точек вокруг их центра – дисперсия, или среднеквадратическое отклонение. Если точки данных близки к среднему, дисперсия будет небольшой. Обобщение дисперсии, при котором центр тяжести заменяется описательной точкой, которая может быть или не быть центром тяжести, используется в кластерном анализе, чтобы указать общее качество разбиения. А именно мера ошибки 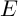 – это сумма всех дисперсий:
– это сумма всех дисперсий:
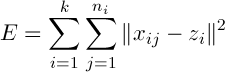 ,
,
где  –
– 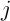 -я точка в
-я точка в 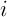 -м кластере,
-м кластере, 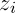 является опорной точкой
является опорной точкой 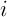 -го кластера, а
-го кластера, а  – число точек в кластере. Обозначение
– число точек в кластере. Обозначение 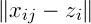 задает расстояние между
задает расстояние между  и
и 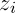 . Таким образом величина ошибки
. Таким образом величина ошибки 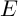 отражает общее рассеяние точек данных вокруг их центров. Для достижения представительной кластеризации, ошибка
отражает общее рассеяние точек данных вокруг их центров. Для достижения представительной кластеризации, ошибка 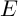 должна быть как можно меньше.
должна быть как можно меньше.
Мера ошибки дает объективный критерий оценки разбиения, а также устраняет плохие разбиения. В настоящее время поиск наилучшего разбиения требует генерации всех возможных комбинаций кластеров и сравнения их меры ошибки.
Рис 2. Парная агломеративная кластеризация
Это может быть сделано для небольших наборов данных с несколькими десятками точек, но не для больших наборов. Число способов представить 1 миллион точек в 256-ти кластерах, например, составляет  . Это число превышает
. Это число превышает  .
.
Кластеризация делается для того, чтобы сократить объем данных. В случае же снимков Landsat поиска наилучшего разбиения не преследуется. Требуется просто разумно сгруппировать данные из N точек в k кластеров, а при необходимости, найти эффективный способ повышения качества исходного разбиения. Для этого имеется семейство алгоритмов итерационных разбиений, которые намного превосходят агломеративный алгоритм, описанный выше.
Итерационные алгоритмы начинаются с выбора k ориентировочных точек, начальные значения которых, обычно, выбираются пользователем. Сначала, исходные данные разбиваются на k кластеров. Точка 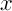 принадлежит кластеру
принадлежит кластеру 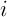 , если
, если 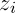 является ближайшей ориентировочной точкой к
является ближайшей ориентировочной точкой к 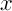 . Позиции ориентировочных точек и присоединение данных к определенному кластеру, регулируются в ходе выполнения итераций. Таким образом, итерационные алгоритмы похожи на процедуру построения, которая начинается с начального «приближения» для каждого параметра, а затем оптимизируется. Алгоритмы этого семейства отличаются методом создания и регулировки разбиений. Три члена этой семьи, обсуждаемые в этой статье – алгоритм Лойда, стандартный алгоритм К-средних, а также непрерывный алгоритм К-средних, впервые описанные в 1967 Дж. Маккуином. Недавно они были адаптированы в Лос-Аламосе для общего пользования.
. Позиции ориентировочных точек и присоединение данных к определенному кластеру, регулируются в ходе выполнения итераций. Таким образом, итерационные алгоритмы похожи на процедуру построения, которая начинается с начального «приближения» для каждого параметра, а затем оптимизируется. Алгоритмы этого семейства отличаются методом создания и регулировки разбиений. Три члена этой семьи, обсуждаемые в этой статье – алгоритм Лойда, стандартный алгоритм К-средних, а также непрерывный алгоритм К-средних, впервые описанные в 1967 Дж. Маккуином. Недавно они были адаптированы в Лос-Аламосе для общего пользования.
Самым простым является алгоритм Лойда. Начальное разбиение происходит так, как описано выше: все точки данных разбиваются на k кластеров по принадлежности к ориентировочным точкам. При корректировке производится расчет центра тяжести для каждого из этих кластеров, а затем полученные центры используются как ориентиры для дальнейшего разбиения исходных точек. Можно доказать, что локальный минимум величины 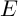 соответствует «центру Вороного», где каждая точка данных более близка к опорной точке своего кластера, чем к любой другой опорной точке. При это каждая опорная точка является центром тяжести своего кластера. Цель итераций состоит в том, чтобы построить разбиение наиболее близкое к такой конфигурации, чтобы ошибка
соответствует «центру Вороного», где каждая точка данных более близка к опорной точке своего кластера, чем к любой другой опорной точке. При это каждая опорная точка является центром тяжести своего кластера. Цель итераций состоит в том, чтобы построить разбиение наиболее близкое к такой конфигурации, чтобы ошибка 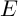 была минимальной.
была минимальной.
Рис 3. Кластеризация алгоритмом K-средних
Для алгоритма Лойда и других итерационных алгоритмов, уточнение разбиения и сходимость ошибки 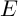 к локальному минимуму происходит довольно быстро, даже при плохо выбранной начальной опорной точке. Однако, в отличие приближений параметров в простой процедуре постройки, в целом это не приводит к тому же набору конечных кластеров. Окончательное разбиение будет лучше, чем первоначальное, но это не обязательно самое лучшее разбиение из множества возможных. Во многих случаях, это не является серьезной проблемой. Например, различия между изображениями Landsat из исходных данных и кластеризованными данными редко заметны даже опытным аналитикам, так что небольшие различия в кластеризованных данных не очень важны. В таких случаях, по мнению аналитиков, лучшим выходом будет метод кластеризации, дающий приемлимые результаты.
к локальному минимуму происходит довольно быстро, даже при плохо выбранной начальной опорной точке. Однако, в отличие приближений параметров в простой процедуре постройки, в целом это не приводит к тому же набору конечных кластеров. Окончательное разбиение будет лучше, чем первоначальное, но это не обязательно самое лучшее разбиение из множества возможных. Во многих случаях, это не является серьезной проблемой. Например, различия между изображениями Landsat из исходных данных и кластеризованными данными редко заметны даже опытным аналитикам, так что небольшие различия в кластеризованных данных не очень важны. В таких случаях, по мнению аналитиков, лучшим выходом будет метод кластеризации, дающий приемлимые результаты.
Стандартный Алгоритм К-средних отличается от алгоритма Лойда более эффективным использованием информации на каждом шаге. Идея обоих алгоритмов одна и та же: выбираются опорные точки и все исходные точки ассоциируются с кластерами. Как и в случае алгоритма Лойда, алгоритм К-средних использует центроиды кластеров в качестве опорных точек для последующего разбиения, но центроиды корректируется во время и после каждого разбиения. Если центр тяжести 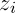 для точки
для точки 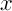 в группе
в группе 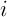 является ближайшей описательной точкой то, никакие коррективы не вносятся, а алгоритм переходит к следующей точке. Однако, если центр тяжести
является ближайшей описательной точкой то, никакие коррективы не вносятся, а алгоритм переходит к следующей точке. Однако, если центр тяжести  кластера
кластера 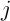 ближе к точке
ближе к точке 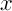 , то
, то 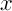 переносится в кластер
переносится в кластер 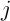 , центроид «усеченного» кластера
, центроид «усеченного» кластера 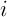 (потерявшего точку
(потерявшего точку 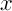 ) и «выращенный» кластер
) и «выращенный» кластер 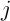 (получившего точку
(получившего точку 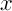 ) пересчитывается, и опорные точки
) пересчитывается, и опорные точки 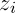 и
и  перемещаются в новые центры тяжести. На каждом шаге каждая из k опорных точек является центороидом или средним, отсюда и название «k-средние». Пример кластеризации с использованием стандартного алгоритма К-средних показан на рисунке 3.
перемещаются в новые центры тяжести. На каждом шаге каждая из k опорных точек является центороидом или средним, отсюда и название «k-средние». Пример кластеризации с использованием стандартного алгоритма К-средних показан на рисунке 3.
Есть несколько модификаций алгоритма К-средних. В некоторых вариантах величина ошибки 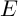 оценивается на каждом шаге, и точка переводится в другой кластер, только если это перераспределение уменьшает величину ошибки
оценивается на каждом шаге, и точка переводится в другой кластер, только если это перераспределение уменьшает величину ошибки 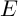 . В оригинальной статье Маккуина о методе «К-средних» центр тяжести обновляется (ассоциация точки с кластером, вычисление центроида, назначения центроида опорной точкой) на каждом шаге. Во всех этих случаях, стандартный алгоритм К-средних требует примерно такое же количество вычислений для одного проход через все точки данных, или одну итерацию, как и алгоритм Лойда. Тем не менее, алгоритм К-средних значительно быстрее, потому что он постоянно обновляет кластеры и не требует столько итераций, как требует менее эффективный алгоритм Лойда.
. В оригинальной статье Маккуина о методе «К-средних» центр тяжести обновляется (ассоциация точки с кластером, вычисление центроида, назначения центроида опорной точкой) на каждом шаге. Во всех этих случаях, стандартный алгоритм К-средних требует примерно такое же количество вычислений для одного проход через все точки данных, или одну итерацию, как и алгоритм Лойда. Тем не менее, алгоритм К-средних значительно быстрее, потому что он постоянно обновляет кластеры и не требует столько итераций, как требует менее эффективный алгоритм Лойда.
Непрерывный алгоритм К-средних
Непрерывный Алгоритм К-средних быстрее, чем стандартная версия и, следовательно, расширяет объем данных, которые могут быть кластерезированы. От стандартного алгоритма он отличается методом выбора начальных опорных точек, и способом выбора данных для процесса обновления. При стандартном подходе начальные опорные точки выбираются более-менее произвольно. В непрерывном алгоритме опорные точки представляют собой случайную выборку из начального множества данных. Если выборка достаточно велика, распределение этих первоначальных опорных точек должно отражать распределение точек во всем наборе. Если весь набор точек плотный, например, в области 7, то образец тоже должен быть плотным в области 7. Когда этот процесс применяется к данным Landsat, он эффективно находит центроиды кластера (и лучшее цветовое разрешение) там, где больше всего сконцентрировано точек.
Еще одно различие между стандартным и непрерывным алгоритмом К-средних в способе обработки данных. Во время каждой полной итерации стандартный алгоритм проверяет все данные точки подряд. С другой стороны, непрерывный алгоритм рассматривает только случайную выборку точек. Если набор данных велик и выборка является репрезентативной, алгоритм должен сходиться гораздо быстрее, чем алгоритм, который проверяет каждую точку по порядку. В действительности, непрерывный алгоритм модифицирует метод обновления центроидов алгоритма Маккуина на этапе инициализации, когда точки исходных данных ассоциируются с кластерами. Как правило, сходимость наступает достаточно быстро, так что второй проход по данным не требуется.
С теоретической точки зрения, случайная выборка представляет собой возврат к первоначальной идее алгоритма Маккуина, как к методу кластеризации данных в непрерывном пространстве. В его формулировке величина ошибки 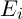 для каждого региона
для каждого региона  определяется по формуле
определяется по формуле
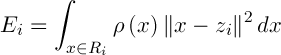 ,
,
где  – непрерывная функция плотности распределения вероятности, а общая мера ошибки задается суммой всех
– непрерывная функция плотности распределения вероятности, а общая мера ошибки задается суммой всех 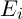 . В идее алгоритма Маккуина используется большой набор дискретных точек, которые могут рассматриваться как большая выборка. Она является хорошей оценкой вероятности
. В идее алгоритма Маккуина используется большой набор дискретных точек, которые могут рассматриваться как большая выборка. Она является хорошей оценкой вероятности  . Становится очевидным, что случайная выборка данных также может быть хорошей оценкой
. Становится очевидным, что случайная выборка данных также может быть хорошей оценкой  . Такой пример дает репрезентативный набор центроидов кластеров и разумную оценку ошибки измерения без использования всех точек в исходном наборе данных.
. Такой пример дает репрезентативный набор центроидов кластеров и разумную оценку ошибки измерения без использования всех точек в исходном наборе данных.
Эти изменения в стандартном алгоритме значительно ускоряют процесс кластеризации. Так как опорные точки и точки данных для обновления отбираются посредством случайной выборки, больше опорных точек будет найдено в плотных регионах исходного набора. Опорные точки будут обновляться в наиболее важных областях. Кроме того, начальные опорные точки уже являются членами набора данных и, таким образом, требуется меньшее количество обновлений. Таким образом, даже при использовании на больших наборах данных, алгоритм, обычно, сходится к решению после небольшого дробления (от 10 до 15 процентов) вычисленных исходных точек. Эта быстрая сходимость отличает непрерывный алгоритм К-средних от менее эффективных алгоритмов. Кластеризация с помощью непрерывного алгоритма К-средних, примерно, в десять раз быстрее кластеризации с помощью алгоритма Лойда.
Время вычислений может сократить, если делать отдельные шаги алгоритма более эффективно. Значительную часть вычислительного времени требующееся для любого из этих алгоритмов кластеризации, как правило, тратится на поиск ближайшей опорной точки к определенной точке из входных данных. В «грубом» методе, расстояния от заданной точки данных до всех опорных точек должны быть рассчитаны и сравнены. Более элегантный метод «локализации точек» избегает этот очень трудоемкий процесс, сокращая число опорных точек, которые необходимо учитывать. Но некоторые время должна быть потрачено на создание структур данных. Такие структуры изменяют исходный порядок опорных точек на «древовидный», в котором опорные точки организованы в категории. Древовидная структура позволяет исключить все категории опорных точек из процедуры вычисления расстояний. Непрерывный Алгоритм К-средних использует древовидный метод для кластеризации трехмерных данных, таких, как цвета пикселей на экране монитора. При использовании на семимерных данных Landsat, алгоритм использует границы одной оси, которая задает порядок опорных точек в направлении максимального изменения. В любом методе необходимо учитывать лишь несколько точек при расчете и сравнении расстояний. Выбор того или иного метода будет зависеть от числа измерений данных.
Две особенности непрерывного алгоритма К-средних – сходимость к правдоподобным группам опорных точек после очень малого числа обновлений и большое сокращение времени вычисления обновлений, что весьма желательно для любого алгоритма кластеризации. На самом деле, такие особенности имеют решающее значение для консолидации и анализа очень больших наборов данных, таких как те, которые обсуждались в сопроводительной статье.
Литература
- James M. White, Vance Faber, and Jeffrey S. Saltzman. 1992. Digital color representation. U.S. Patent Number 5,130,701.
- Stuart P. Lloyd. 1982. Least squares quantization in PCM. IEEE Transactions on Information Theory IT-28: 129–137.
- Edward Forgy. 1965. Cluster analysis of multivariate data: Efficiency vs. interpretability of classifications, Biometrics 21: 768.
- J. MacQueen. 1967. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Volume I, Statistics. Edited by Lucien M. Le Cam and Jerzy Neyman. University of California Press.
- Jerome H. Friedman, Forest Baskett, and Leonard J. Shustek. 1975. An algorithm for finding nearest neighbors. IEEE Transactions on Computers C – 24: 1000–1006. [Single-axis boundarizing, dimensionality.]
- Jerome H. Friedman Jon Louis Bentley, and Raphael Ari Finkel. 1977. An algorithm for finding best matches in logarithmic expected time. ACM Transactions on Mathematical Software 3: 209–226. [Tree methods.]
- Helmuth Spath. 1980. Cluster Analysis Algorithms for Data Reduction and Classification of Objects. Halsted Press.
- Anil K. Jain and richard C. Dubes. 1988. Algorithms for Clustering Data. Prentice Hall.
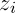 для кластера
для кластера 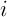 , как правило, является центром тяжести кластера. В случае одномерных данных, таких как результаты тестов, центр тяжести – это среднее арифметическое значений точек в кластере. Для многомерных данных, где каждая точка имеет несколько измерений, центр тяжести будет иметь одинаковое число компонент и каждая компонента будет средним арифметическим соответствующих составляющих точек кластера.
, как правило, является центром тяжести кластера. В случае одномерных данных, таких как результаты тестов, центр тяжести – это среднее арифметическое значений точек в кластере. Для многомерных данных, где каждая точка имеет несколько измерений, центр тяжести будет иметь одинаковое число компонент и каждая компонента будет средним арифметическим соответствующих составляющих точек кластера.

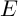 – это сумма всех дисперсий:
– это сумма всех дисперсий: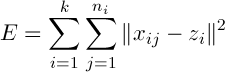 ,
, –
– 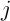 -я точка в
-я точка в  – число точек в кластере. Обозначение
– число точек в кластере. Обозначение 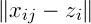 задает расстояние между
задает расстояние между 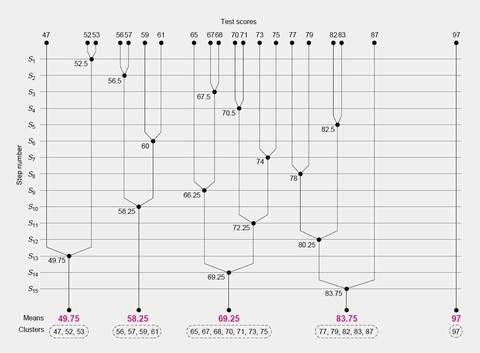
 . Это число превышает
. Это число превышает  .
.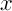 принадлежит кластеру
принадлежит кластеру 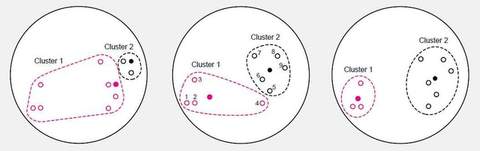
 кластера
кластера 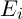 для каждого региона
для каждого региона  определяется по формуле
определяется по формуле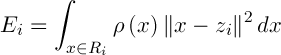 ,
, – непрерывная функция плотности распределения вероятности, а общая мера ошибки задается суммой всех
– непрерывная функция плотности распределения вероятности, а общая мера ошибки задается суммой всех