Назад в библиотеку

УДК 004.054

ПРИМЕНЕНИЕ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ К ГЕНЕРАЦИИ ТЕСТОВ ДЛЯ ТЕСТИРОВАНИЯ ПРОГРАММ ПО КРИТЕРИЮ C1

Ерёмичев В. В., Савкова Е.О.
Донецкий национальный технический университет кафедра автоматизированных систем управления.
E-mail: v.eremichev@gmail.com

Аннотация:

Ерёмичев В.В., Савкова Е.О. Применение генетических алгоритмов к генерации тестов для тестирования программ по критерию С1.Рассмотрена задача тестирования ветвей программы. Приведен пример построения управляющего графа на основании программы и преобразования его в расширенный автомат. Описан принцип нахождения значений переменных с помощью генетического алгоритма. Рассмотрены особенности генетического алгоритма для представленной задачи.

Постановка проблемы

В тестировании программного обеспечения существует ряд задач, которые являются трудоемкими и громоздкими, а следовательно они требуют автоматизации. Одной из таких задач является генерация тестовых наборов. Тестовые наборы создаются на основе критерия тестирования согласно заданным спецификациям программы. Суть проблемы состоит в том, чтобы автоматически получать набор значений переменных, которые бы позволили протестировать программу в соответствии с определенным критерием тестирования. В этой задаче был выбран критерий C1 - критерий тестирования ветвей программы. Следовательно, задача заключается в том, чтобы автоматически получать набор значений, которые бы позволили протестировать программную ветку. Полнота покрытия тестирования достигается степенью оттестированности всех ветвей.Статья содержит краткий обзорметода, который может быть использован для создания тестового набора для прохождения ветви программы.

Обзор метода построения тестируемой модели

Для решения поставленной задачи предлагается использовать возможности расширенных конечных автоматов для создания модели тестируемой программы на основе управляющего графа, и генетические алгоритмы для автоматизации создания тестов. К примеру, имеется код программы, которая по значению целого числа должна печатать его простую характеристику – ноль это, четное или нечетное число, положительное или отрицательное.

Управляющий граф программы (УГП) на рисунке 1 отображает поток управления программы. Нумерация узлов графа совпадает с нумерацией строк программы.

Рисунок 1 – Управляющий граф программы

Предлагаемый подход подразумевает максимальную формализацию спецификаций. В свою очередь управляющий граф программы можно представить в виде конечного расширенного автомата, содержащего переменные и охранные условия на переходах.Все требования спецификации должны быть выполнены во время корректной работы программы. Автомат реагирует на события и выполняет переходы в зависимости от значений переменных автоматной модели, которые используются в охранных условиях на переходах. Вид автомата представлен на рисунке 2.

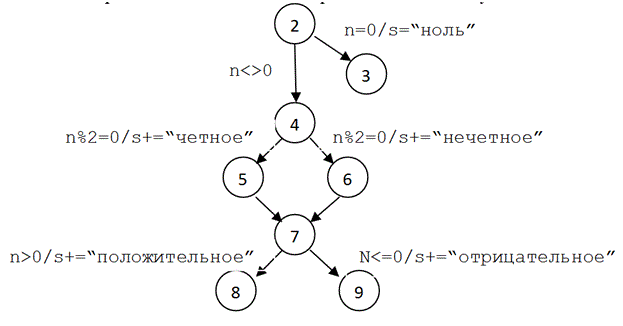
Рисунок 2 – Конечный расширенный автомат.

Представление теста в виде последовательности событий и набора значений внешних переменных удобно с точки зрения автоматического создания кода теста, однако неудобно и неясно для разработчика, который основывается на спецификации, написанной на естественном языке. Поэтому разработчик записывает тест как последовательность переходов в модели. В этом случае возникает задача поиска последовательности событий и набора значений внешних переменных, соответствующих заданной последовательности переходов в модели. Ниже изложен принцип решения этой задачи, основанный на использовании генетических алгоритмов.

Последовательность событий однозначно определяется по последовательности переходов. Сложнее подобрать значения переменных – они должны удовлетворять ряду требований. Во-первых, охранные условия на всех переходах в описанном пути должны быть выполнены. Во-вторых, все требования спецификации объектов управления должны выполняться, так как при реальном использовании значений этих переменных будут приходить из объектов управления с данными спецификациями. В предложенном подходе генетические алгоритмы применяются для решения задачи поиска набора значений, при котором будет выполнен заданный путь в расширенном конечном автомате. Такую задачу можно свести к задаче оптимизации.

Построение оптимизационной задачи

Мы имеем набор внешних переменных, задействованных на выбранной последовательности переходов. Этот набор можно рассматривать как вектор значений внешних переменных <x1, x2, …, xn >, где xi – значение внешней переменной, а n – число внешних переменных для этого пути.Для использования оптимизационных алгоритмов необходимо определить функцию приспособленности – функцию, которая оценивает, насколько хромосома решает проблему, и позволяет выбирать лучшие решения из всего поколения. В данной задаче функция приспособленности на вход принимает вектор значений и выдает число, характеризующее приспособленность этого вектора для выполнения заданного пути. Чем меньше это число, тем больше подходит данный вектор значений. Таким образом, задача поиска подходящего набора значений внешних переменных сводится к задаче оптимизации, где требуется найти вектор, которому соответствует минимальное значение функции приспособленности.

Для данной задачи хромосома будет представлять собой вектор значений внешних переменных, состоящий из одного элемента – переменной n. Для общего случая один ген является значением одной переменной для заданного пути. Скрещивание происходит классическим одноточечным способом. Мутация представляет собой замену произвольного гена случайным значением из области допустимого диапазона значений.

Однозначного способа определения функции приспособленности не существует. Тем не менее, существует критерий, который называется расстоянием до условия (Branchdistance), для определения приспособленности хромосом. Расстояние до условия позволяет оценить, насколько близка была данная хромосома к выполнению конкретного условия, которое на практике не было выполнено. Например, для условия A > B, расстояние до условия будет вычисляться по формуле |A - B|. Чем меньше значение |A - B|, тем ближе значение A к B и тем ближе хромосома к тому, чтобы это условие было выполнено. Если условие выполнено, то расстояние до условия ноль. При этом расстояние до условия можно представить как (1)

(1)

Функция приспособленности, основанная на использовании критерия расстояние до условия, успешно применяется для поиска значений для выполнения пути в расширенном конечном автомате, причем эти значения являются граничными для условия, что увеличивает уверенность в правильности тестируемой программы.

Для последовательности переходов может быть задано большое число условий, поэтому расстояние до условия всего пути необходимо вычислять по отдельности, рассматривая условия на каждом переходе этого пути. Каждый переход описывается набором параметров:

• Событие, по которому этот переход может произойти.
• Охранное условие, которое должно быть выполнено для совершения перехода.
• Действия на переходе: вызов методов объектов управления, получение значений внешних переменных из среды или изменение значений переменных модели.
• . Предусловия перехода, включающие в себя требования спецификации программы, которые должны быть выполнены для выполнения перехода, и требования спецификации объектов управления, которые должны быть выполнены для вызова методов объектов управления, задействованных при переходе.
• Постусловия перехода, включающие в себя требования спецификации программы и ее объектов управления.

Таким образом, даже в рамках одного перехода может быть задействовано большое число условий. Для более точного вычисления расстояния до условия перехода в работе каждый переход разбивается на несколько меньших шагов. После этого исходная последовательность переходов рассматривается как последовательность шагов. Оценка приспособленности всей последовательности шагов вычисляется как сумма оценок для каждого шага по-отдельности. Каждый шаг оценивается по формуле вычисления расстояния для условия. Отметим, что шаги выполняются последовательно и что выполненность шагов в начале пути важнее, чем в его конце. Например, если выполнены условия всех шагов, кроме первого, то сумма расстояний до условия будет небольшой, так как для всех, кроме первого шага, это значение будет равно нолю. На практике эта хромосома не позволяет пройти ни одного шага, так как для того, чтобы успешно пройти второй шаг, необходимо выполнить все условия на первом шаге. Поэтому в предложенном подходе расстояния до условия шагов суммируются с учетом местоположения этих шагов в пути – используется взвешенная сумма (2) приспособленности пути

(2)

где m– число шагов в пути, m=n*3, здесь n– число переходов в пути;
f_i– расстояние до условия для i-го шага.
d_i– вес i-го с шага, d_i=(m-i)²

Если для одного шага задано несколько условий, то расстояние до условия этого шага вычисляется как сумма расстояний до условия каждого из этих условий.

Выводы

В рамках данной статьи был предложен подход к тестированию ветвей программ, предполагающий автоматизированную генерацию тестов на основе расширенных конечных автоматов. В статье проиллюстрированы такие достоинства как: Удобство использования расширенных конечных автоматов для построения модели тестируемой программы. Автоматизация поиска значений внешних переменных при помощи применения генетических алгоритмов. Таким образом, генетические алгоритмы считаются полезными для решения оптимизационных задач.

Литература

Wegener J., Buhr K., Pohlheim H., Automatic test data generation for structural testing of embedded software systems by evolutionary testing /In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2002). NY: Morgan Kauf-mann. 2002, pp. 1233–1240.
Pargas R. P., Harrold M. J., Peck R. R. Test-data generation using genetic algorithms
Кулямин В.В., Тестирование на основе моделей.
Монахов А., Петренко А., Бритвина Е., Петренко О., Грошев С. Тестирование на основе моделей.