ПРИМЕНЕНИЕ МУРАВЬИНЫХ АЛГОРИТМОВ ДЛЯ ПОИСКА ОПТИМАЛЬНЫХ МАРШРУТОВ ГРУЗОПЕРЕВОЗОК
Семенюта E.В., Привалов М.В.
Донецкий национальный технический университет
Источник: Інформаційні управляючі системи та комп'ютерний моніторинг (ІУС та КМ - 2011) / Матеріали II
науково-технічної конференції студентів, аспірантів та молодих вчених. —
Донецьк, ДонНТУ — 2011, с. 199-203.
Аннотация:
Семенюта Е.В., Привалов М.В. Применение
муравьиных алгоритмов для поиска оптимальных маршрутов грузоперевозок.
Рассмотрена и формализована задача поиска оптимальных маршрутов
курьерской доставки грузов. Обоснован и выбран в качестве метода решения
муравьиный алгоритм. Предлагается использование локального
лексикографического поиска для учета порядка обхода городов.
Введение
Динамика расширения рынка
транспортно-логистических услуг, наблюдаемая в последнее время, открытие
новых логистических терминалов, усиление соперничества между
операторами способствуют росту потребности в решении
транспортно-логистических задач в целях более эффективного обслуживания
клиентов. Одной из таких задач является оптимальное планирование
маршрутов грузовых перевозок, решение которой заключается в решении так
называемой задачи коммивояжера (TSP) - задачи комбинаторной оптимизации.
Задача последовательного упорядочения
(ЗПУ) была первоначально решена как ограниченная версия асимметричного
TSP (ATSP). Первая математическая модель для ЗПУ была введена в [1], где
был предложен подход секущих плоскостей, чтобы вычислить более низкие
границы на оптимальном решении. В [2] был описан метод Лагранжа
relax-and-cut, и были определены новые действительные усечения для
получения более сильных низких границ.
Позже, основываясь на многогранном
исследовании, выполненном на задачах ATSP с ограничениями
предшествования [3], в [4] предложен новый класс действительных
неравенств и описан алгоритм branch-and-cut для широкого класса случаев
ЗПУ. Эти эвристики не содержат ограничения напрямую: в результате
невозможные решения просто отвергнуты. При таком подходе [4] удалось
вычислить новые верхние оценки для проблемы ЗУП в TSPLIB, хотя
генетический алгоритм, называемый Maximum Partial Order/Arbitrary
Insertion (MPO/AI), предложенный в [5], возможно работает лучше в том же
классе задач. MPO/AI всегда работает в пространстве допустимых решений
путем введения сложных операторов скрещивания, что сохраняет общую схему
из двух родителей путем определения их максимального частичного порядка
через матричные операции [6].
Общая постановка проблемы
Для планирования маршрутов курьерской
доставки грузов необходимо решить задачу последовательного упорядочения
пунктов следования.
В каждом областном центре Украины
существует склад, который использует некоторое количество транспортных
средств поставки с идентичной грузоподъемностью Q.
На N складах есть груз весом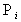 ,
,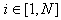 .
На каждом i-м складе,
.
На каждом i-м складе,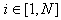 , имеется Z заказов весом
, имеется Z заказов весом ,
, .
Требуется составить маршруты доставки грузов с одних складов на другие в
течение 48 часов, причем выгрузка и дозагрузка могут осуществляться на
складах по пути следования транспортного средства.
Дан полный взвешенный граф из вершин N.
Вершинам графа сопоставим склады, на которых имеется груз, ребрам -
пути, ведущие от склада к складу, и припишем им стоимость пути
.
Требуется составить маршруты доставки грузов с одних складов на другие в
течение 48 часов, причем выгрузка и дозагрузка могут осуществляться на
складах по пути следования транспортного средства.
Дан полный взвешенный граф из вершин N.
Вершинам графа сопоставим склады, на которых имеется груз, ребрам -
пути, ведущие от склада к складу, и припишем им стоимость пути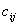 .
Решение для задачи маршрутизации транспорта может быть представлено в
виде перевозок всего имеющегося на всех складах груза K маршрутами
{R1...Rk}, К --> min.
Задача оптимизации грузовых перевозок может быть сформулирована как
минимизация общей стоимости всех маршрутов с учетом выполнения
ограничений:
.
Решение для задачи маршрутизации транспорта может быть представлено в
виде перевозок всего имеющегося на всех складах груза K маршрутами
{R1...Rk}, К --> min.
Задача оптимизации грузовых перевозок может быть сформулирована как
минимизация общей стоимости всех маршрутов с учетом выполнения
ограничений:
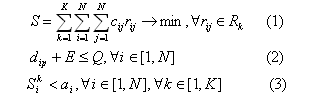
где 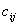 - вес ребра, ведущего из вершины i в вершину j,
- вес ребра, ведущего из вершины i в вершину j,  – подмаршрут от склада i к складу j,
– подмаршрут от склада i к складу j,
 - соответствующий маршрут, где
- соответствующий маршрут, где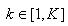 , К – количество маршрутов, Е – вес уже имеющегося груза в автомобиле.
, К – количество маршрутов, Е – вес уже имеющегося груза в автомобиле.
Ограничение (2) определяет, что
транспортное средство не может быть загружено больше, чем позволяет его
грузоподъемность.
 – вес р-го груза на i-м складе,
– вес р-го груза на i-м складе, 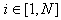 , N – количество складов,
, N – количество складов,  , Z – количество грузов на складе.
Ограничение (3) – это ограничение по времени; прибытие машины на склад не должно быть позднее установленного срока.
, Z – количество грузов на складе.
Ограничение (3) – это ограничение по времени; прибытие машины на склад не должно быть позднее установленного срока.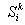 – это время прибытия соответствующей k-й машины на i-й склад,
– это время прибытия соответствующей k-й машины на i-й склад, – крайний срок времени обслуживания i-го склада.
– крайний срок времени обслуживания i-го склада.
Задача последовательного упорядочения
также может быть сформулирована, как общий случай ассиметричной задачи
коммивояжера, основываясь только на весах узлов.
В этой интерпретации 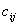 - вес ребра (i,j), где
- вес ребра (i,j), где 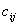 может отличаться от
может отличаться от  , и этот вес может представлять собой стоимость ребра (i,j), если
, и этот вес может представлять собой стоимость ребра (i,j), если 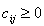 , или ограничение на порядок обхода, при
, или ограничение на порядок обхода, при 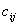 =-1. Значение
=-1. Значение 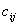 =-1 означает, что узел i должен предшествовать узлу j, причем, необязательно последовательно.
=-1 означает, что узел i должен предшествовать узлу j, причем, необязательно последовательно.
Решение задачи
Рассматриваемая задача относится к
NP-сложным задачам комбинаторной оптимизации, для которых
нецелесообразно находить оптимальное решение. К таким задачам разумно
применять эвристические алгоритмы, которые быстро находят хорошие, хотя и
не обязательно оптимальные, решения.
Можно попробовать связать с
метаэвристикой локальную оптимизацию. Это интересное сочетание, так как
локальный оптимизатор часто страдает от проблемы "инициализации", кроме
того, локальная процедура поиска тратит много времени, улучшая низкое
начальное качественное решение [16]. Поэтому интересно найти хорошие
метаэвристические локальные оптимальные сцепления, где сцепление хорошо,
если метаэвристика генерирует начальные решения, которые можно отнести к
очень хорошим локальным оптимумам локальным оптимизатором. Необходимо
решить задачу последовательного упорядочения (SOP) с помощью
муравьиного алгоритма в сочетании с модифицированной версией 3-х
оптимальной процедуры поиска.
Задача последовательного упорядочения
может быть сформулирована как общий случай ассиметричной задачи
коммивояжера (за исключением того, что маршрут не обязательно должен
быть замкнутым).
В данной работе предлагается решить задачу с помощью муравьиного алгоритма.
Каждый муравей многократно начинает
движение с узла 0 и добавляет новые узлы, пока все узлы не были
посещены, и узел n достигнут. Находясь в узле і, муравей выбирает
вероятностно следующий узел j из набора F (i) из выполнимых узлов. F (i)
сдержит все узлы j, которые еще должны быть посещены, и все, что должны
предшествовать j, согласно ограничениям предшествования, были уже
вставлены в последовательность.
Система выбирает с вероятностью 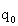 узел с лучшим
узел с лучшим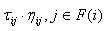 (детерминированное правило), в то время как с вероятностью
(детерминированное правило), в то время как с вероятностью , узел выбран согласно вероятностному правилу, которое одобряет узлы, связанные ребрами с более высокими значениями
, узел выбран согласно вероятностному правилу, которое одобряет узлы, связанные ребрами с более высокими значениями 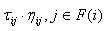 [15].
[15].
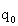 основан на параметре S, который является числом узлов. S позволяет системе определить
основан на параметре S, который является числом узлов. S позволяет системе определить 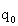 независимо от задачи, измеряя его таким образом, что ожидаемое число узлов, отобранных с вероятностным правилом, является S.
независимо от задачи, измеряя его таким образом, что ожидаемое число узлов, отобранных с вероятностным правилом, является S.
Как только каждый муравей построил
выполнимое решение, к нему применяют локальный поиск. В локальном
масштабе оптимальные решения используются, чтобы обновить следы феромона
на дугах, согласно правилу испарения следа феромона. В нашем случае
только лучший муравей - муравей, который построил самый короткий тур,
может отложить след феромона. Объяснение этому - то, что таким образом
"привилегированный маршрут" запоминается в матрице следов феромона, и
будущие муравьи будут использовать эту информацию, чтобы произвести
новые решения в соседстве этого привилегированного маршрута.
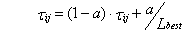 (6)
где
(6)
где 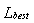 - самый короткий путь, полученный с начала вычисления (путь самого лучшего муравья).
- самый короткий путь, полученный с начала вычисления (путь самого лучшего муравья).
След феромона также испаряется в
течение построения решения. В этом случае, однако, он удален из
посещенных ребер. Другими словами, каждый муравей, перемещаясь из города
i в город j, применяет правило испарения феромона, которое заставляет
количество следа феромона на ребре (і,j) уменьшаться [15]. Правило:
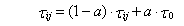 (7)
где
(7)
где  - первоначальное значение следов. Считается, что хорошее значение для этого параметра
- первоначальное значение следов. Считается, что хорошее значение для этого параметра
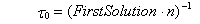 (8)
(8)
Объяснение использования формулы (7) -
то, что муравьи съедают след феромона, в то время как они строят
решения так, чтобы определенное множество в произведенных решениях было
точно.
Далее для того, чтобы учесть
ограничения на порядок обхода городов (узлов графа) будет применен
лексикографический поиск. Который будет заключаться в следующем. Берем
найденную ранее последовательность узлов и получаем новую посредством
обмена узлов в ней так, как это было предложено Дориго и Гамбарделла в
[16]. Проходим все узлы и инвертируем те из них, которые стоят не в
нужном порядке. Для этого генерируем 2 пути (левый и правый), которые
первоначально составлены из одного единственного узла и расширяются
добавлением одного нового узла на каждом шаге. Эта особенность позволяет
легко проверить выполнимость решения, потому что условия
предшествования должны быть проверены только для нового добавленного
узла. Будем различать прямой и обратный поиск. Процедура поиска
начинается, устанавливая узел h=0, и затем перемещает h через
последовательность, пока узел n-2 не достигнут. Каждый раз, когда узел h
отобран, процедура выполняет прямой и обратный лексикографический поиск
того же самого h.
Процедура прямого лексикографического
3-opt поиска начинается установкой значения i, которое определяет самый
правый узел левого пути (path_left), и выполняется цикл на значение j,
которое определяет самый правый узел правого пути (path_right)(Рис. 1а и
1б): path_right=(i+1,...j) итерационно расширяется новым ребром
{j,j+1}[16].
Когда все возможные узлы добавлены в
правый путь, левый путь расширяется новым ребром {i,i+1} (Рис. 1в). И
поиск снова начинается в правом пути. Левый и правый пути при
инициализации состоят только из элементов i=h+1 и j=i+1 (Рис. 1г).

Рисунок 2. Прямой лексикографический 3-opt поиск
В случае обратного поиска (Рис. 2)
левый путь идентифицируется (j+1, ..., i) и правый (i+1, ..., h). После
установки h, i=h-1 и j=i-1 (Рис. 2а), и расширяем левый путь
перемещением j до начала последовательности, присваивая j значения i-2,
i-3, ..., 0 (Рис. 2б). Затем правый путь итерационно расширяется в
обратном порядке новым ребром {i,i+1}, и цикл в левом пути повторяется.
Полный лексикографический поиск
посещает все возможные узлы последовательности, но он должен быть
остановлен, как только находит невыполнимый обмен. Левый путь должен
быть определен как (h+1, ..., i), тогда правый путь будет j=i+1. В этой
ситуации возможно проверить обменную выполнимость, проверяя, есть ли
отношение предшествования между узлом j и узлами в правом пути. Перед
расширением правого пути новым ребром {j,j+1} мы проверяем, выполнимы ли
все еще результирующие пути, проверкой отношения предшествования между
новым узлом j+1 и узлами в левом пути. В случае, если проверка не
выполняется, поиск останавливается.
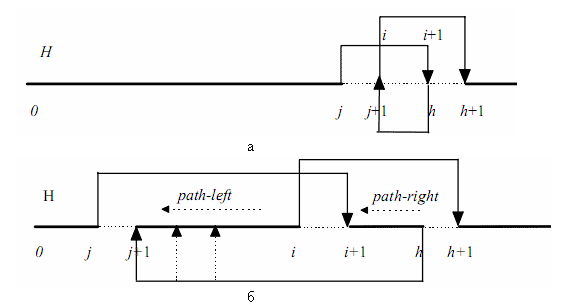
Рисунок 3. Обратный лексикографический 3-opt поиск
Выводы
Анализ, проведенный в работе, показал,
что задача грузоперевозки с дозагрузкой по пути следования может быть
формализована как асимметричный случай задачи коммивояжера с
дополнительными ограничениями на направленность маршрута.
Предложен способ решения задачи с
применением муравьиного алгоритма. Показано, что учет направленности
маршрута может быть выполнен с применением локального
лексикографического 3-opt поиска, предложенного в [6]. Направлением
дальнейшей работы является реализация данного метода и его
экспериментальное исследование в рамках поставленной задачи.
Литература
- Ascheuer N., Escudero L. F., Grotschel M. and Stoer M.,
1993, A Cutting Plane Approach to the Sequential Ordering Problem (with
Applications to Job Scheduling in Manufactoring), SIAM Journal on
Optimization 3,25–42.
- Escudero L.F., Guignard M., Malik K, 1994. A Lagrangian
Relax-and-cut Approach for the Sequential Ordering Problem with
precedence Relationships, Annals of Operations Research 50, 219–237.
- Balas E., Fischetti M., Pulleyblank W.R., 1995, The
Precedence-constrained Asymmetric Traveling Salesman Polytope,
Mathematical Programming 65, 241–265.9. Costa D. and A. Hertz, 1997,
Ants Can Colour Graphs, Journal of the Operational Research Society, 48,
295–305.
- Ascheuer N., 1996. Hamiltonian Path Problems in the On-line Optimization of Flexible
Manufacturing Systems. ZIB Technical Report TR 96-3.
- Chen S. and Smith S., 1996, S.F. Commonality and Genetic
Algorithms. Carnegie Mellon University, The Robotic Institute, Technical
Report CMU-RI-TR-96-27.
- Gambardella L.M., Dorigo M. HAS-SOP Hybrid Ant System for the Sequential Ordering Problem, Technical Report IDSIA 11-97.
- Штовба С.Д. Муравьиные алгоритмы// Exponenta Pro. Математика в приложениях. 2004. 4(4)
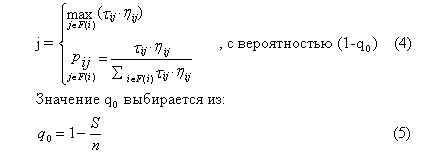
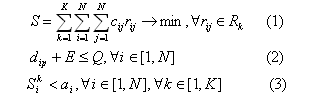
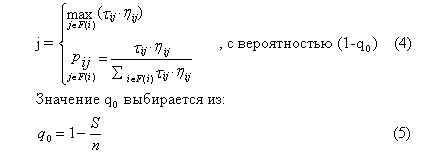
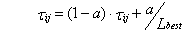 (6)
где
(6)
где 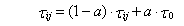 (7)
где
(7)
где 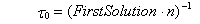 (8)
(8)



