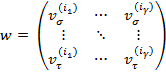Коваленко А.А., Секирин А.И. - Прогноз многомерных временных рядов в рамках задачи прогнозирования отказов вентиляционного оборудования.

Аннотация

Коваленко А.А., Секирин А.И. Прогноз многомерных временных рядов в рамках задачи прогнозирования отказов вентиляционного оборудования. Рассмотрены существующие методы прогнозирования многомерных временных рядов. Определены средства для решения задачи прогнозирования отказов вентиляционного оборудования. Проанализированы реализации данных методов, рассмотрены пакеты прикладных программ, реализующие требуемую функциональность. Создана и протестирована своя реализация выбранного метода.

Актуальность задачи

Задача анализа временных рядов представляет собой весьма актуальную проблему в различных областях науки и техники. В частности, задачей такого типа является прогнозирование времени отказов шахтного вентиляционного оборудования. Поскольку от его исправности зависит безопасность рабочих, решение задачи прогнозирования отказов является приоритетным, к тому же позволит планировать время ремонта и закупок нового оборудования. В настоящее время диагностика оборудования производится, как правило, при помощи анализа спектрограмм вибросигналов, снятых в различных точках. Это приводит к задаче анализа многомерных временных рядов. Обработка многомерных данных, включающая хранение, передачу по каналам связи, задачи классификации и прогнозирования, представляет определенные трудности[1]

Поскольку под вентиляционным оборудованием понимают несколько групп оборудования (вентиляторы, электродвигатели, воздушные фильтры, шумоглушители, а также их составные части: подшипники, муфты и др.), для решения задачи необходимо разработать универсальный алгоритм, позволяющий быстро обрабатывать поступающие данные, либо набор алгоритмов для каждой группы оборудования.

Существующие методы, модели, алгоритмы, применяемые для решения задачи

Существующие методы прогнозирования многомерных временных рядов можно разделить на следующие группы:

Статистические методы. К ним относятся простейшие методы, строящие прогноз на основе усредненного значения за некоторый период. Методы обладают низкой точностью, поскольку не учитывают наличие тренда, сезонности, аномальных выбросов в исходных данных.
Регрессионные методы. В данную группу методов, кроме собственного регрессионных методов, принято включать методы авторегрессии и их модификации, такие как интегрированная модель авторегрессии – скользящего среднего (ARIMA). Данные методы являются более точными по сравнению со статистическими методами, но также являются неустойчивыми к выбросам. Обычно, перед использованием данных методов, производится сокращение размерности задачи при помощи одного из существующих методов, например метода главных компонент, дискретно-косинусного преобразования, быстрого преобразования Фурье, факторного анализа и других [2]. Но в рамках данной задачи сокращение размерности приведет к потере некоторого количества информации, что является недопустимым.
Вейвлет-преобразования. В основе данной группы методов лежит основное свойство вейвлетов – возможность анализа различных частотных компонент ряда. В настоящее время данные преобразования используются для прогнозирования одномерных временных рядов, как и все вышеперечисленные группы методов. Математический аппарат, позволяющий анализировать многомерные ряды, еще разрабатывается. Следует заметить, что выбор вейвлет-функции также представляет определенную сложность.[3]
Нейросетевые модели. Являются мощным и гибким инструментом прогнозирования многомерных временных рядов, поскольку структура нейронной сети может быть изменена в зависимости от типа оборудования. К недостаткам можно отнести необходимость наличия достаточно большого количества данных для обучения сети, что является затруднительным в случае, например, установки более нового оборудования.[4]
Генетические алгоритмы. В основе обучающегося алгоритма LGAP (Learning Genetic Algorithm for Prognosis) лежит идея, ранее использованная в алгоритмах ZET и WANGA, которые, как правило, используются для заполнения пропусков в эмпирических таблицах данных. Данный алгоритм лишен недостатков описанных выше алгоритмов, однако требует большое количество системных ресурсов для своей работы. Алгоритм легко распараллеливается и показывает хорошие результаты при работе на многопроцессорных системах, но такое решение является весьма дорогостоящим.[5]
Сингулярный анализ временных рядов (SSA). В настоящее время обычно применяют модификацию данного метода, называемую «гусеницей», которая легко обобщается на любое число измерений. Данный алгоритм является двухпараметрическим (задается длина гусеницы и число ее компонент). Выбор параметров оказывает значительное влияние на результат, а также время работы алгоритма. Особо следует выделить устойчивость алгоритма к выбросам, что является важным в рамках рассматриваемой задачи, поскольку датчик, снимающий спектрограмму вибросигнала, является очень чувствительным. Хорошо справляется с прогнозированием нестационарных временных рядов, что также является преимуществом.[6]

Математическая постановка задачи

Пусть наблюдается система функций 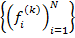, где

k – номер ряда. k = 1 .. s.

s – число временных рядов.

N – длина временного ряда.

i – номер отсчета.

Рядом в данном случае является спектрограмма вибросигнала, снятая в определенной точке. Требуется разложить в ряд сумму компонент, интерпретировать каждую и построить продолжение ряда по выбранным компонентам.

Алгоритм SSA

В результате применения метода ряд раскладывается на простые компоненты: тренды, сезонные, периодические и колебательные составляющие, а также шумовые компоненты. Полученное разложение может служить как для прогноза ряда в целом, так и отдельных его компонент.

Алгоритм состоит из трех этапов:

Построение матрицы наблюдений.
Анализ главных компонент.
Прогноз.

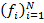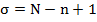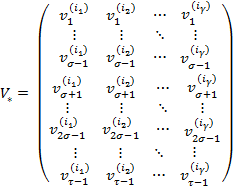
Для упрощения рассмотрим одномерный временной ряд . Выберем n такое, что 0 < n < N - 1 – время жизни гусеницы. Пусть – длина гусеницы. Построим последовательность Z из n векторов в пространстве 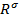следующего вида:

Будем называть Z нецентрированной матрицей наблюдений. В случае многомерного ряда матрицей наблюдений называется столбец из матриц наблюдений, соответствующий каждой из компонент.

Рассмотрим ковариационную матрицу полученной выборки:

Выполним ее сингулярное разложение (SVD):

V – ортогональная матрица собственных векторов:

Далее рассмотрим систему главных компонент:

После проведения анализа, следует восстановить матрицу наблюдений по главным компонентам:

Далее восстанавливаются исходные последовательности:

Затем начинается прогнозирование. Числовой ряд 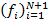называется продолжением ряда 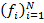, если порождаемая им при гусеничной обработке выборка лежит в той же гиперплоскости, что и у исходного ряда. Ранее был вычислен набор главных компонент 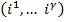. Определим:

Также определим:

Тогда прогнозируемое значение в точке N + 1 вычисляется по формуле:

Была выполнена программная реализация вышеописанного алгоритма на объектно-ориентированном языке высокого уровня C#.

Эксперементальные исследования

Алгоритм был протестирован как на относительно простых последовательностях, так и на зашумленных нестационарных рядах с изменяющейся периодичностью, и показал хорошие результаты прогнозирования, устойчивость к выбросам. Ошибка прогноза составляет не более 3-5%. На рисунке 1 приведен график прогноза потребления электричества по дням недели.

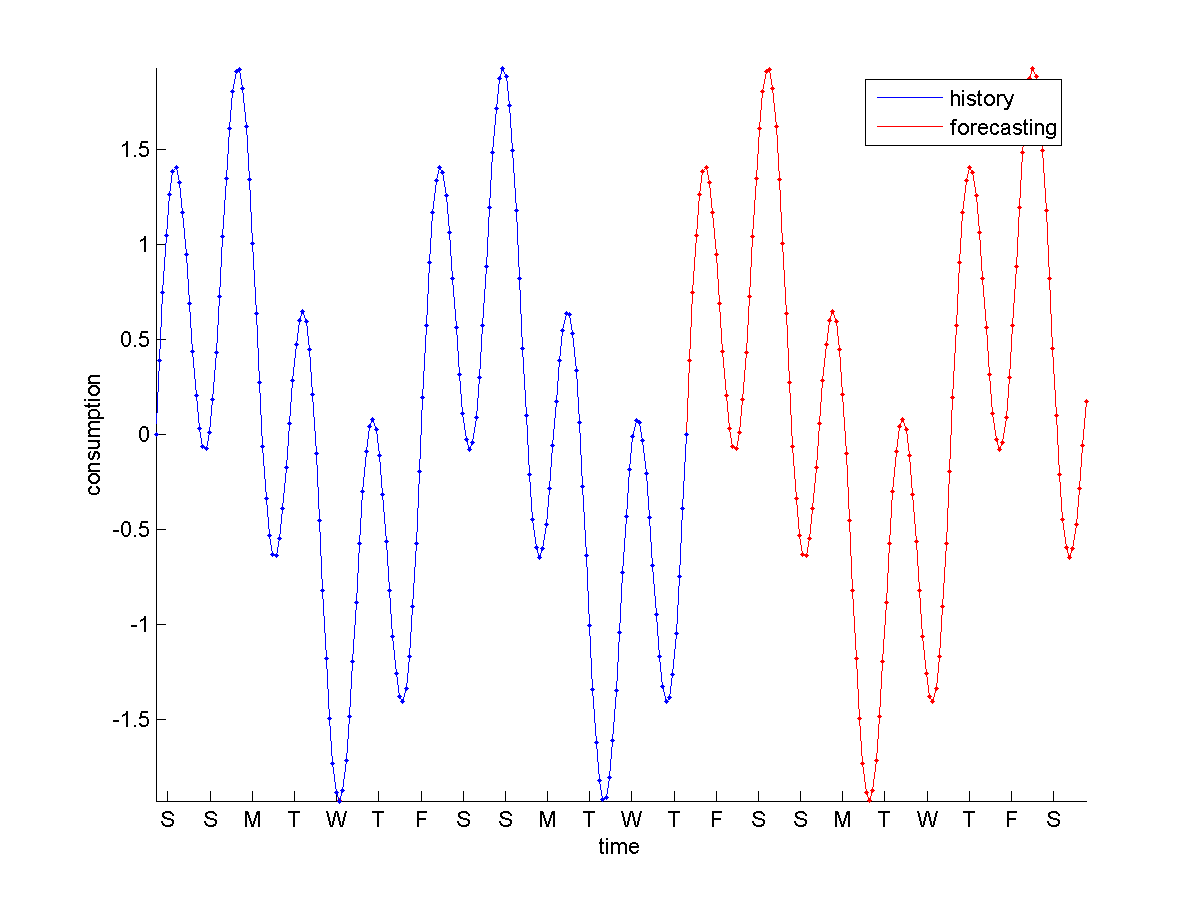
Рисунок 1 – График прогноза потребления электричества по дням недели

Выводы

Был проведен обзор существующих методов решения задачи прогнозирования многомерных временных рядов. Их основными недостатками являются:

неустойчивость к выбросам, нарушениям периодичности ряда, шумам;
не позволяют анализировать нестационарные временные ряды;
алгоритмы, предназначенные для анализа одномерных временных рядов, могут давать неверный прогноз, поскольку не учитывают факт многомерности исходного ряда.

Алгоритм SSA лишен этих недостатков, а также обладает рядом преимуществ:

нетребователен к системным ресурсам;
некоторые базовые части алгоритма (метод главных компонент, работа с матрицами) уже реализованы в виде бесплатных библиотек, соответственно, реализация упрощается;
нет необходимости в обучении;
позволяет анализировать отдельные компоненты ряда (например, только тренд, что может быть полезно для анализа спектрограммы).

Была выполнена программная реализация алгоритма на языке C#. При проведении экспериментов ошибка прогноза не превышала 5%, что является допустимым при решении поставленной задачи.

Список использованной литературы

Хеннан Э. Многомерные временные ряды / Э. Хеннан. — М.: Мир, 1974. — 576 с.
Большаков А.А. Методы обработки многомерных данных и временных рядов / А.А. Большаков, Р.Н. Каримов. Учебное пособие для вузов — М.: Горячая линия — Телеком, 2007. – 522 с.
Nason G.P. The stationary wavelet transform and some statistical applications / G.P. Nason, B.W. Silverman — N.Y.: Springer, 1995. — 464 p.
Шибалкин А.А. Прогнозирование временных рядов с использованием многослойных нейронных сетей и вейвлет-преобразований / А.А. Шибалкин, М.В. Марковский — М.: Научная сессия МИФИ – 2008. — Том 11. — 412 с.
Загоруйко Н.Г. Прикладные методы анализа данных и знаний / Н.Г. Загоруйко — Новосибирск: ИМ СО РАН, 1999. – 270 с.
Прогнозирование временных рядов методом SSA. [Электронный ресурс]. – Режим доступа: http://www.machinelearning.ru/....
Метод гусеницы [Электронный ресурс]. – Режим доступа: http://www.gistatgroup.com.