Аннотация
Sinha P. Нейросетевой автоматический генератор тестовых последовательностей. В данной статье обсуждается методика моделирования задачи генерации тестов с использованием нейронных сетей. С помощью примеров, показано представление цифровых схем как сети Хопфилда, перевод неисправностей к ней и генерация тестовых векторов для нее. Полученные результаты ясно указывают на преимущество в использовании ее в качестве средства распараллеливания процессов генерации тестов. Кроме того, обсуждаются более быстрые способы реализации минимизации энергии с использованием квадратичного бинарного программирования.
1. Введение
Автоматическая генерация тестовых последовательнотей для большинства комбинационных схем часто тестируется на СБИС. Таким образом, распараллеливание процесса может сократить время тестирования. Для реализации этого, задача тестирования должна быть сопоставлена с параллельной моделью вычислений. Нейронные сети представляют собой сложные нелинейные функции. В данных исследованиях были использованы Сети Хопфилда. Они представляют собой попытку смоделировать нервную систему нашего организма. Нейроны изображены в виде набора узлов, связанных двунаправленной линией веса Tij. Каждый узел имеет активное состояние V, связанное с ним, и порог I. Сеть находится в возбужденном состоянии, если при случайном обновлении нейронов, согласно правилу обновления:
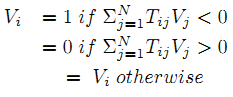
ее состояние изменяется в зависимости от состояния соседей. Где N — число узлов в сети, а энергия Е определяется:

где K — константа.
Если состояние не изменяется по правилу обновления, то сеть находится в стабильном состоянии. Хопфилд показал, что в стабильном состоянии энергия минимальна. Следовательно, такая нейронная сеть может быть использована для моделирования задач оптимизации по определению энергетической функции надлежащим образом и позволяет сети стабилизировать случайное обновление узлов. Это присуще распараллеливанию в модели.
Веса сети Хопфилда определяются обучением векторных последовательностей, которые поступают на сеть, которая выбирает схему AND, OR, NOT, NAND или NOR, заданную простыми функциями:
- AND

- OR
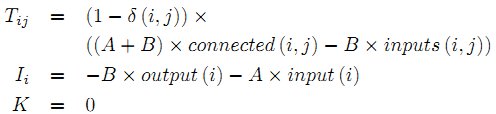
- NAND

- NOR
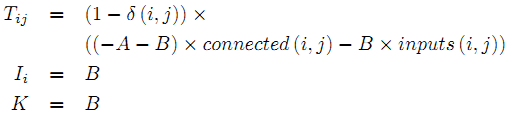
- NOT

где функции:

Эта идея представления использования для АТГН определяется в [1]. Раздел I посвящен истории идеи нейронных сетей, используемых для автоматической генерации тестовых последовательностей. Раздел II показывает пример того, как нейронная сеть может быть использована для генерации тестов. Раздел III — описание и раздел IV — заключение.
2. История вопроса
Нейронные сети были объектом изучения с 1940-х годов. Сети Хопфилда — примерно с 1982 года. Их уникальность заключается в том, что они являются рекуррентными сетями, т. е. имеют обратную связь с выхода на вход, которая имитирует ассоциативный характер нейронов в мозгу точнее, чем сети с обратным распространением. Сетями Хопфилда была решена проблема определения рекуррентной нейронной сети, которая стабилизируется. К 1985 году стало известно, что сети Хопфилда могут быть использованы для решения задач комбинаторной оптимизации. Задача заключается в моделировании такой проблемы с точки зрения сети Хопфилда (рис. 1).
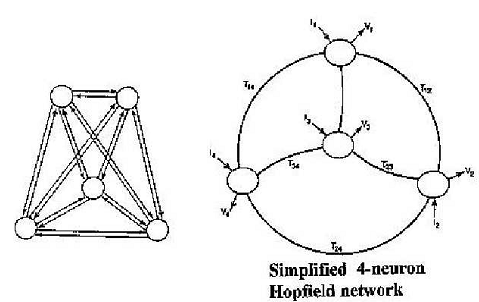
Рисунок 1 – Сеть Хопфилда
В области тестирования, в попытках сократить время тестирования СБИС, основные усилия прилагаются для распараллеливания задачи генерации тестов для того, чтобы сократить это время. Технический отчет «Автоматическая генерация тестов с использованием нейронных сетей», 1988 года является самым ранним, который я мог найти, в котором упоминается использование нейронных сетей для генерации тестов.Следующие публикации [2], [3], [8] собраны в книге [1]. Первоначально использование техники градиентного спуска для минимизации функции энергии применялось для моделирования константных неисправностей. Позже, минимизация была сделана быстрее, используя идею вывода графов. Транзитивное замыкание и пути сенсибилизации могли обнаружить избыточные неисправности, а также модели задержки тестов. Последняя публикация — в [11]. Далее методы вывода графов были представлены В.Д. Агравалем.
3. Анализ и алгоритмы
Чтобы использовать нейронные сети для генерации тестов, тестируемая схема должна быть представлена в виде нейронной сети. После этого следующий шаг, моделируется неисправность в схеме. Если это возможно, узлы с одинаковым порогом входа и выхода будут объединены в шаге нейронного сокращения. Затем, минимизация энергии будет генерировать тест для неисправной схемы. После всего этого, производится оптимизация для затрачивания минимума усилий для генерации тестов. В следующих разделах переход на эти шаги производится на примере схемы, изображенной на рис. 2.

Рисунок 2 – Пример схемы
Эта схема имеет в общей сложности 16 состояний неисправности, m-s-a-0 и c-s-a-0 являются избыточными, а (b-s-a-0, a-s-a-1, l-s-a-1, m-s-a-1, c-s-a-1, d-s-a-1) и (b-s-a-1, a-s-a-0, l-s-a-0, d-s-a-0) эквивалентны.
Состояния «нет неисправности» b-s-a-0 b-s-a-1 a-s-a-0 a-s-a-1 l-s-a-0 l-s-a-1 m-s-a-0 m-s-a-1 c-s-a-0 c-s-a-1 d-s-a-0 d-s-a-1.
b=0 1 1 0 0 1 0 1 1 1 1 1 0 1
b=1 0 1 0 0 1 0 1 0 1 0 1 0 1
Представление цифровой схемы как нейронной сети.
Использование функций для порогов и активации значений, приведенных выше, а также принимая схему на рис. 2 в качестве образца, вес и пороговые значения были рассчитаны и показаны на рис. 3.
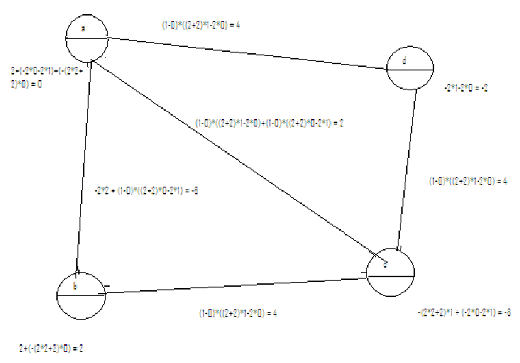
Рисунок 3 – Пример схемы, представленной как сеть Хопфилда
4. Представление неисправности в схеме
Используя ту же схему, неисправность l-s-a-1 представлена как показано на рис. 4. Для неисправного узла, создается двойной узел a''. Все узлы, связанные с a' выходами схем AND подключены к узлу a с состоянием «нет неисправности». Все узлы, связанные с а в качестве входных данных подключены к узлу a'', который в состоянии неисправности. В результате на рис. 5, сеть с исправными, и неисправными значениями.
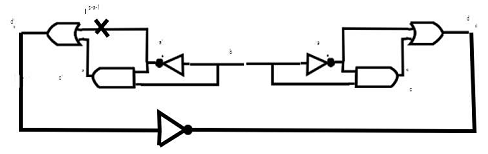
Рисунок 4 – Пример схемы c l-s-a-1 неисправнотью

Рисунок 5 – Сеть Хопфилда c l-s-a-1 неисправнотью
5. Генерация тестов
Для того, чтобы создать тест, энергия системы должна быть сведена к минимуму, что произойдет в случае стабильного состояния. Энергия схемы формулируется следующим образом:
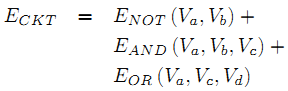
Правило обновления для каждой случайной перестановки узлов задается:

Где Ek для каждого из узлов:
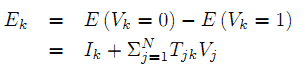
Теперь, чтобы задать действительное значение на рис. 2, мы начнем сначала с активация значениями 0 для каждого из нейронов.
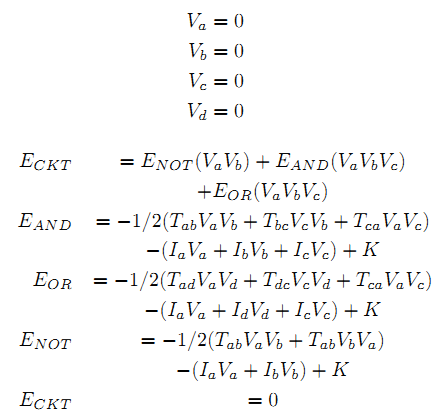
Затем мы случайно перестанавливаем, тот или иной нейрон и определяем, что обновленное б переходит в состояние 1, которое дает энергию для схемы, составляющую -2, что меньше, чем 0 и, следовательно, получаем значения Va = 0 , Vb = 1, Vc = 0, Vd = 0.
Это известно как метод градиентного спуска с итеративной релаксацией. Таким же образом, последовательное задание получено для нейронной сети, описанной неисправной схемой на рис. 5.
6. Результаты
Результаты, описанные в [1] ясно показывают преимущества использования этой модели для генерации тестов и являются эффективным способом распараллелить схемы. Они показывают, что менее чем за 1 сек берется для тестирования либо схема Шнайдера, 4-битный параллельный сумматор (SN5483A) или ECAT. В симуляторе «нет неисправности» количество тестов меньше, чем количество тестов, т. е. векторов тестов компактных до определенной степени (рис. 6).
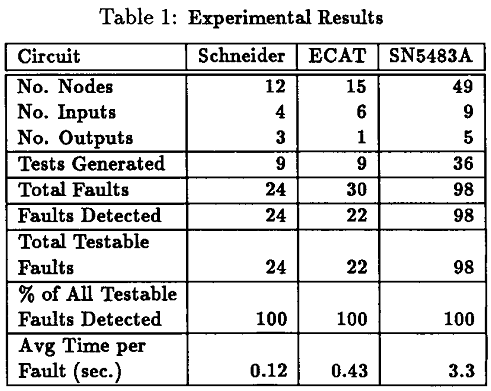
Рисунок 6 – Результаты, опубликованные с помощью техники градиентного спуска
по С. Чакрадару, В.Д. Агравалу, М.Л. Бушеллу
7. Выводы
Таким образом, этот метод, безусловно, действующий и работоспособный для генерации тестов. Это приводит не только к решению задачи тестирования, но и оказывает влияние на другие поля.
Список использованной литературы
1. Neural Models and Algorithms for Digital Testing, Srimat T Chakradhar, Vishwani D. Agrawal, Michael L. Bushnell, Kluwer Academic Publishers.
2. Automatic Test Generation Using Neural Networks , Srimat T Chakradhar, Michael L. Bushnell, Vishwani D. Agrawal.
3. Toward Massively Parallel Automatic Test Generation, SRIMAT T. CHAKRADHAR, MICHAEL L. BUSHNELL, VISHWANI D. AGRAWAL.
4. NEUDEM Neural network based decision making for generating tests in digital circuits. Suresh Rai, H. Lee Johnson, and Vijay Ratnam.
5. Generalized Hop?eld Neural Network for Concurrent Testing, Julio Ortega, Alberto Prieto, Antonio Lloris, and Francisco J. Pelayo.
6. Neural Networks As Massively Parallel Automatic Test Pattern Generators, A. Majumder, R. Dandapani.
7. Neural Models for Transistor and Mixed-Level Test Generation, Carolina L. C. Cooper, Michael L. Bushnell.
8. Redundancy Identi?cation Using Transitive Closure. Vishwani D. Agrawal, Michael L. Bushnell, Qing Lin.
9. COGENT: Compressing and compacting GEnetic algorithms and Neural networks based automatic Test generator, Shekhar Agrawal Sharad.
10. HIERARCHICAL, TEST GENERATION USING NEURAL NETWORKS FOR DIGITAL CIRCUITS, Pan Zhongliang, IEEE Intl. Conf. Neural Networks and Signal Processing.
11. Neural Network Model for Testing Stuck-at and Delay Faults in Digital Circuit, Pan Zhongliang, VLSID’04.
12. A Transitive Closure Algorithm for Test Generation,S. T. Chakradhar, V. D. Agrawal and S. G. Rothweiler, IEEE Trans. CAD, vol. 12, no. 7, pp. 1015-1028, July 1993.
13. FIRE: A Fault-Independent Combinational Redundancy Identi?cation Algorithm,M. A. Iyer and M. Abramovici, IEEE Trans. VLSI Systems,vol. 4, no. 2, pp. 295-301, June 1996.
14. Redundancy Identification in Logic Circuits using Extended Implication Graph and Stem Unobservability The-orems, V. J. Mehta, Masters Thesis, Rutgers University, Dept. of ECE, New Brunswick, NJ, May 2003.
15. Using Contrapositive Rule to Enhance the Implication Graphs of Logic Circuits,K. K. Dave, Masters Thesis, Rutgers University, Dept. of ECE, New Brunswick, NJ, May 2004.
16. Using Contrapositive Law in an Implication Graph to Identify Logic Redundancies.Kunal K. Dave, Vishwani D. Agrawal, Michael L. Bushnell.VLSI Design 2005: 723-729.
17. A Fault-Independent Transitive Closure Algorithm for Redundancy Identification.Vishal J. Mehta, Kunal K. Dave, Vishwani D. Agrawal, Michael L. Bushnell, VLSI Design 2003: 149-154.
18. Neural Net and Boolean Satis?ability Models of Logic Circuits. IEEE Design and Test. Volume 7 , Issue 5 (September 1990), Srimat Chakradhar, Vishwani Agrawal, Michael Bushnell, Thomas Truong.
19. A New Transitive Closure Algorithm with Application to Redundancy Identification, Vivek Gaur.
20. Three-valued Neural Networks for Test Generation.H. Fujiwara. In Proceedings of the 20th IEEE International Symposium on Fault Tolerant Computing, pages 64-71, June 1990.