Аннотация
Дорогов А.Ю., Алексеев А.А. Структурные модели и топологическое проектирование быстрых нейронных сетей В статье рассматриваются структурные и топологические модели многослойных быстрых нейронных сетей (БНС). Используется математический аппарат отображений числовых множеств и теории линейных представлений. Предложен алгоритм проектирования топологий БНС.
Введение
Быстрые нейронные сети [1]являются разновидностью многослойных нейронных сетей прямого распространения. БНС сопоставимы с обычными нейронными сетями примерно в том же отношении как алгоритмы быстрого преобразования Фурье (БПФ) с прямым дискретным преобразованием Фурье. Высокая вычислительная эффективность БНС достигается за счет разумных ограничений на структурную организацию нейронной сети.
Структура БНС в какой-то мере повторяет структуру нейронных сетей живой природы, для которых всегда существуют ограничения на размерности рецепторных полей и на связи между нейронами. В работе [2] было показано что вопросы структурной организации БНС следует рассматривать на двух уровнях: уровне структурной модели БНС и уровне топологической реализации БНС. Если уровень структурной модели определяет общие свойства БНС по размерностям рецепторных полей и структуре межслойных связей, то уровень топологии определяет конкретную аппаратную или программную реализацию нейронной сети. Оба эти уровня рассмотрения неразрывно связаны между собой.
Структурная модель БНС
На рис.1 показан пример БНС в классическом представлении где каждая вершина соответствует одному нейрону, а дуги определяют связи между нейронами. Такое представление в дальнейшем будем называть топологической реализацией структурной модели. На рис.2 приведена структурная модель, построенная для данной сети. Каждой вершине структурной модели соответствует группа нейронов, имеющих общее рецепторное поле. Эти группы нейронов были названы нейронными ядрами. На структурном уровне каждое нейронное ядро характеризуется размерностью рецепторного поля и числом входящих в него нейронов. Эта пара чисел задает вес вершины структурной модели. Нейронное ядро j в слое m описывается оператором Amj, осуществляющего преобразования входного вектора собственного рецепторного поля:

Рисунок 1 – Топологическая реализация структурной модели
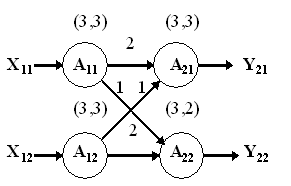
Рисунок 2 – Структурная модель, построенная для данной сети
В матричном представлении оператор нейронного ядра можно записать в виде:

где Wmj — матрица синаптических весов ядра, F( ) — многомерная функция активации, компонентами которой являются функции активации отдельных нейронов ядра. Действие оператора нейронного ядра определено на паре градуированных [3] векторных пространств: пространстве рецепторов и пространстве нейронов слоя. Связи между слоями задаются проектирующими операторами, сохраняющими условия градуировки. Ранг проектирующего оператора определяет вес дуги структурной модели. Принципиальной особенностью построения БНС является независимость рецепторных полей ядер, т.е. рецепторные поля нейронных ядер не пересекаются.
Структурная модель является по существу описанием целого класса эквивалентных топологических реализаций БНС. Можно сказать, что множество топологий формирует орбиту структурной модели на множестве матричных представлений. Топология БНС задается числовыми частичными отображениями (частичными подстановками) [4]:
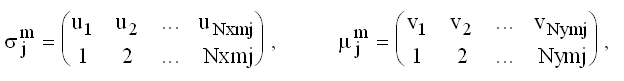
где Nxmj — размер рецепторного поля ядра j в слое m, Nymj — число нейронов в ядре j слоя m. u — номер базисного вектора в пространстве рецепторов, v — номер базисного вектора в пространстве нейронов.
Действие частичных подстановок определено на входном и выходном векторах нейронного слоя, частичная подстановка σmj выделяет рецепторное поля ядра, а подстановка μmj нейронное поле. Формально действие частичных подстановок записывается в виде:

Комбинации символов *σmj, и *μmj можно рассматривать и как символическое обозначение проектирующих операторов, однако запись в виде формального произведения дает ряд преимуществ при математических выкладках. По принципу построения БНС проектирующие операторы не пересекаются, поэтому σmα ∧ σmj = 0, μmα ∧ μmj = 0 для любых j ≠ ∞.
Смежные нейронные слои связаны между собой перестановочными операторами перехода, действие которых определено подстановками qm:

Операторы межслойного перехода индуцируют локальные операторы связи между нейронными ядрами, так что

где ρmij — частичные подстановки соответствующие локальному оператору, Σ — символ прямой суммы векторов.
На уровне структурной модели каждая локальная связь характеризуется рангом проектирующего оператора. Числовое значение ранга определяет вес соответствующей дуги структурной модели (рис 2). Из выражений (1)—(3) следует:

Это выражение определяет рекуррентный алгоритм построения топологии нейронной сети.
Топологическая реализация БНС
Топологию нейронной сети компактно можно представить в виде произведения матиц смежности графа топологической реализации. Например, топологии нейронной сети, показанной на рис.1 отвечает произведение матриц вида:
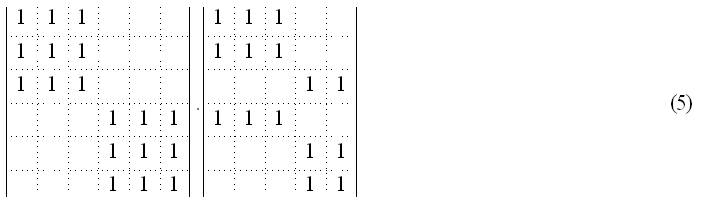
Такие матрицы будем называть топологическими. Позиции ненулевых элементов в данных матрицах определяются частичными подстановками σmj , μmj . Нетрудно заметить, что при произвольной перестановке элементов в любой строке частичных подстановок σmj , μmj топологические матрицы не изменяются. Неоднозначность в выборе частичных подстановок можно устранить если ограничиться множеством подстановок в которых отсутствуют инверсии [5]. При этом элементы строк будут всегда упорядочены по возрастанию.
При отсутствии инверсий отпадает необходимость в отображении вторых строк подстановок поскольку они всегда будут упорядочены по возрастанию. Таким образом расположение нейронного ядра в топологической матрице достаточно задать парой упорядоченных множеств Umj , Vmj, образующих верхние строки частичных подстановок σmj , μmj. Введенные множества будем называть топологическими. Учитывая сказанное, построим удобный для программной реализации алгоритм построения топологии БНС. Приведем вначале описание алгоритма, а затем покажем, что он удовлетворяет общему соотношению (4).
Пусть для вершин Amj топология задается парами (Umj,Vmj), а для вершин слоя m+1 парами (Um+1j,Vm+1j). Структурные связи между двумя смежными слоями запишем в виде ранговой матрицы:

где rji — ранги проектирующих операторов межслойных связей. Каждой вершине слоя m соответствует строка ранговой матрицы, а каждой вершине слоя m+1 столбец матрицы. Сумма элементов строки i равна порядку множества Vmi, а столбца j — порядку множества Um+1j. Введем в рассмотрение числовое множество Tm={1,2,...,Nm}, где Nm=card(Tm) = ΣiΣjrmij . (Нетрудно проверить, что значение Nm равно числу нейронов в слое m и совпадает с размерностью рецепторного поля слоя m+1. Разместим элементы множества Tm в виде матрицы (рис 3.), подобной по структуре матрице Rm, причем размещение выполним так чтобы выполнялось условие card(Tmij)=rmij. Подмножество элементов принадлежащих i-ой строке обозначим TAi , а j-ому столбцу TBj. Введем две произвольные подстановки на множестве Tm, которые обозначим qA и qB. Тогда алгоритм построения топологических множеств будет определяться правилом:

Графически алгоритм можно представить схемой, показанной на рис. 3.

Рисунок 3 – Алгоритм построения топологических множеств
Покажем теперь, что данный алгоритм удовлетворяет соотношению (4). Из схемы рис. 3 следует:
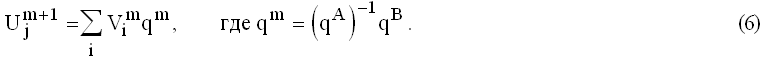
Поскольку
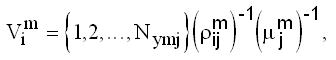
а также
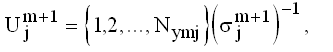
то из (6) получим

Обращение последнего выражения, очевидно, приводит к (4). Использование двух подстановок qA и qB вместо одной qm делает алгоритм симметричным и более удобным при реализации.
Если
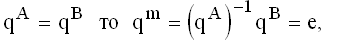
где е — тождественная подстановка.
Будем называть топологию для которой последнее равенство выполнено компактной и расширенной в противном случае. Для расширенной топологии между топологическими матрицами смежных слоев необходимо вводить перестановочную матрицу, соответствующую подстановке qm. В общем случае для задания топологии необходимо фиксировать подстановки qA , qB и размещение множества Tm. При хранении топологии можно без потери информации сократить объем данных, если предварительно произвести «нормализацию» размещения множества Tm, следуя одному из ниже приведенных правил:
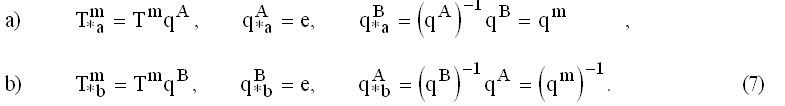
Здесь символ «*» указывает значение после нормализации, а символы «a,b» варианты нормализации. Если топология компактная тогда нормализация любого типа приводит к равенству qA*=qB*=e . Таким образом для компактной топологии достаточно хранить только размещение множества Tm , а для расширенной — размещение Tm и подстановку qm Покажем, что оба варианта нормализации эквивалентны, для этого выполним над нормализованным представлением по типу «*a» выполним нормализацию типа «*b»

Таким образом, мы приходим к нормализованному представлению типа «*b», определяемом правилом (7). Повторение нормализации типа «a» возвращает нас к исходному состоянию.
В качестве примера рассмотрим построение топологий для структурной модели показанной на рис. 2. Ниже приведены ранговая матрица и схемы построения двух вариантов топологии:

Подмножества U1i, V2j можно выбрать произвольно. Выберем их равными U11=(123), U12=(456), V21=(123), V22=(456), в этом случае топологические матрицы первого варианта точно соответствуют представлению (5). Для второго варианта выбрано qA = e,
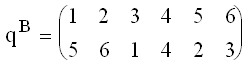
и сохранены прежние значения U1i, V2j. Расширенная топология для этого случая имеет следующее матричное преставление:

От расширенной топологии всегда можно перейти к компактной, выполнив умножение левой или правой смежной топологической матрицы на перестановочную, очевидно, что при этом информация о подстановке qm теряется и поэтому обратный переход будет неопределен.
Выводы
В данной работе представлены два уровня структурного описания БНС: структурная модель и топологическая реализация. Показано, что адекватным инструментом проектирования топологий является математический аппарат числовых частичных отображений. На основе этого аппарата предложен машинно-ориентированный алгоритм построения топологий БНС. Топологическое проектирование позволяет оптимальным образом выбрать программную или аппаратную реализацию БНС из класса эквивалентных.
Список использованной литературы
1. Дорогов А.Ю., Алексеев А.А. Структурные модели быстрых нейронных сетей. В сб. «Интеллектуальные системы» /Труды II-го Международного симпозиума, под ред. К.А. Пупкова, т.2 — М.: Из-во ПАИМС. 1996, с.138-143
2. Дорогов А.Ю., Алексеев А.А. Математические модели быстрых нейронных сетей. В сб. научн. тр. СПбГЭТУ «Системы управления и обработки информации». Вып.490, 1996, с.79-84
3. А.И. Кострикин, Ю.М. Манин. Линейная алгебра и геометрия. — М.:— «Наука» — 1986.— 304с
4. Мальцев А.И. Алгебраические системы. — М.:— Наука, 1970
5. Кострикин А.И. Введение в алгебру. Основы алгебры. — М.:— Физматлит. 1994, — 320с