Особенности представления постбинарных вещественных чисел в контексте интервальных вычислений и развития аппаратного обеспечения средств компьютерного моделирования

А.Я. Аноприенко, С.В. Иваница, С.В. Кулибаба

Введение

На сегодняшний день аппаратное обеспечение компьютеров в состоянии производить всевозможные вычисления с числами, которые могут быть представлены всего в двух форматах — целые числа и числа с плавающей запятой. Именно вычисления с плавающей запятой являются основой современного компьютерного моделирования. Для представления действительных чисел (чисел с плавающей запятой) в двоичном коде используется разработанный ассоциацией IEEE (Institute of Electrical and Electronics Engineers)

стандарт для двоичной арифметики с плавающей точкой (IEEE Standard for Binary Floating-Point Arithmetic, ANSI/IEEE Std 754-1985).

В ряде работ [1-3] было отмечено несовершенство стандарта IEEE 754-1985, и на многих примерах показано, как использование стандарта IEEE 754 может привести к множественным ошибкам компьютерных вычислений. В качестве основных ошибок, вызванных применением чисел в формате IEEE 754-1985 можно назвать ошибки связанные с точностью представления вещественных чисел, с неправильным приведением типов данных, а также вызванные сдвигом мантисс и округлением [1]. В 2008 году ассоциация IEEE выпустила расширенный стандарт IEEE 754-2008, который без

изменения включил в себя стандарт 1985 года и дополнил его форматом учетверенной точности. Но введение нового формата не позволило решить основные проблемы, связанные с появлением грубых ошибок в вычислениях [3], что является главной предпосылкой для существенной модификации всей системы компьютерных вычислений с целью повышения ее надежности и адаптации к современным требованиям, особенно с точки зрения компьютерного моделирования.

 

Постбинарное представление вещественныхчисел

 

В современных условиях в качестве одного из решений проблем, связанных с форматом представления чисел с плавающей запятой может выступать дальнейшее развитие как логической, так и вычислительной составляющей современного компьютинга [4]. В работе [3] были предложены способы для преодоления проблем, связанных с ограничением разрядности чисел, поскольку использование при вычислениях разрядности, существенно превышающей стандартную, приводит к получению правильных результатов. К таким способам можно отнести операции, приводящие к увеличению (или выравниванию) разрядности во избежание переполнения порядка результата и выполнения корректных вычислений, выполнение отложенного деления (числитель и знаменатель вычисляются отдельно, а деление откладывается на заключительный этап вычислений), а также использование интервальных вычислений [5, 6].

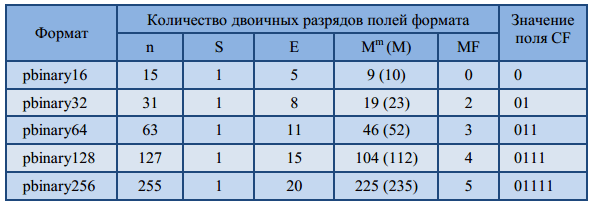
Реализация подобных операций была заложена в разработку постбинарных методов вычислений, основанных на постбинарном представлении количественных значений [4, 7]. Поэтому на основании форматов чисел различной точности стандарта IEEE754- 2008 было предложено пять постбинарных форматов, общая схема полей которых представлена на рис. 1, а размерность полей — в табл. 1.

Для обеспечения совместного гибкого использования различных форматов чисел с плавающей запятой вводится поле идентификатора формата, для которого в стандартных форматах могут быть задействованы часть младших разрядов мантиссы M и которое в общем случае состоит из кода (определителя формата числа) CF и модификатора MF формата. Мантисса, уступившая часть младших разрядов для значений полей CF и MF становится модифицированной

Mm. По значениям поля MF формат числа уточняется и может быть представлен как «парный формат», в котором путем удвоения каждого из разрядов в виде единого «постбинарного значения» представляются пары чисел, интерпретируемые либо как числитель и знаменатель обыкновенной дроби, либо как граничные значения интервалов (для поддержки интервальных вычислений) [3].

Рисунок 1 — Предлагаемые варианты модифицированных форматов чисел с плавающей запятой (S, Е, M^m — знак, порядок и мантисса числа, MF, CF — модификатор и формат числа, n — номер старшего бита формата)

 

Таблица 1 — Разрядность полей постбинарныхформатов чисел (в скобках возле количества разрядов модифицированной мантиссы M^m приведено количество разрядов традиционной мантиссы М числа соответствующей точности)

Разработка преобразователя постбинарного числа

 

На основании разработанных форматов представления вещественных чисел, средствами языка VHDL [8] описана модель устройства, выполняющего преобразование чисел в условный постбинарный тип данных (одно значение сформированного тетракода [9] условно кодируется одним двоичным разрядом) с дальнейшим использованием полученного формата в интервальных вычислениях. Фактически разработан алгоритм преобразования одного постбинарного числа, которое, в конечном счете, представляет собой значения границ интервала. Структура модели представлена на рис. 2.

 

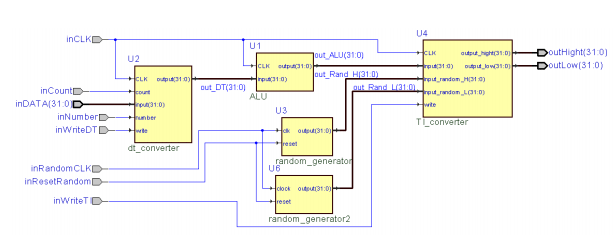
Рисунок 2 — Схема преобразователя (dt_converter – блок преобразования входного вещественного числа в постбинарное, TI_converter – блок разложения постбинарного числа на границы интервала, ALU – арифметико-логическое

устройство; random_generator – генератор псевдослучайных чисел)

 

Рассмотрим работу модели. Пусть на входную 32-разрядную шину inDATA поступило, например, двоичное значение десятичной дроби 0,123456789. Однако данное число не может быть точно представлено в формате одинарной точности (Single), соответствующего стандарту IEEE754-2008, и после обратного преобразования в десятичный формат, в окне Windows будет возвращено число 0,1234568 (по результатам работы программы IEEE754 v.1.00 [10]), а действительное представление полученного числа (возвращенное из Single) будет следующим:

+0,12345679104328155517578125.

Полученное число несет в себе ошибку точности представления вещественного числа формата Single. Во избежание такого рода ошибок, в блоке dt_converter происходит преобразование бинарного числа в постбинарное, в котором каждый бит заменяется значением тетракода, отображающего одно из четырех состояний тетралогики: логические ноль и единица, состояния множественности (многозначности) и неопределенности [11]. Причем значения множественности заносятся в те разряды мантиссы, начиная с которых возникает возможная ошибка округления (номер бита, с которого начинаются разряды множественности, и количество таких разрядов поступают на соответствующие входы inNumber и inCount блока dt_converter). Младшие разряды, начиная от последнего разряда множественности, заполняются значениями неопределенности, поскольку уже не являются значащими. Так, двоичное представление

числа 0,123456789 в 32-разрядном формате с плавающей запятой выглядит следующим образом (значение на шине inDATA):

0 01111011 11111001101011011101010.

После обработки в блоке dt_converter на шину outDT поступает постбинарное число, которое имеет следующий вид:

0 01111011 11111001101011011MMAAAA.

В блоке TI_converter происходит разбиение полученного постбинарного числа на два бинарных, представляющих собой границы интервального результирующего числа. Процедура перехода постбинарного числа в интервальное происходит по принципу, описанному в [12]. При этом все разряды множественности заменяются либо двоичным «0» для формирования левой (нижней) границы интервала, либо двоичной «1» для формирования правой (верхней) границы интервала. Значения неопределенности для каждой границы заполняются случайными двоичными значениями, которые формируются в соответствующих генераторах псевдослучайных чисел. Полученные значения границ интервала поступают на соответствующие 32-разрядные выходные шины outLow и outHight. Блок ALU разработан для реализации логических и арифметических операций над постбинарными числами.

На рис. 3 представлена временная диаграмма работы модели данного устройства, из которой видны все промежуточные значения и значения результирующего интервала (подчеркнутые поля чисел могут быть заполнены случайным набором двоичных значений):

[0 01111011 11111001101011011001111; 0 01111011 11111001101011011110111].

Преобразовав данный интервал в 10 с/с, получим следующую пару значений:

[0,1234566; 0,1234569],

представляющих собой границы интервала, имеющего достаточно узкую ширину wid = 2,458692e-07.

При этом выполняется следующее условие:

0,123456789 ?[0,1234566; 0,1234569],

свидетельствующее о том, что полученный интервал представляет исходное число, являющееся элементом множества R действительных чисел, на множестве IR интервальных чисел.

Рисунок 3 — Временная диаграмма работы преобразователя

Заключение

В докладе предложен последовательный переход к различным представлениям числа (от десятичного к интервальному через постбинарное) и модель соответствующего преобразователя, на вход которого поступают десятичные числа, все внутренние вычислительные операции выполняются с постбинарными числами, а в качестве результата выступает интервальное число, гарантировано включающее в себя точное значение выполненных операций.

Для устранения необратимых погрешностей, возникающих в ходе вычисления и приводящих к неверному результату предложены модификации стандарта форматов представления чисел от половиной точности до октоточности.

В ходе работы модели вычислительное устройство, в качестве преобразователя чисел, показало высокую точность работы. В дальнейшем планируется разработка алгоритмов работы с вещественными тетракодовыми и интервальными числами, которые будут составлять основу построения постбинарного микропроцессора.

 

Список литературы

 

1. Яшкардин В.Л. IEEE 754 — стандарт двоичной арифметики с плавающей точкой. [Электронный ресурс]. Страница доступа: http://www.softelectro.ru/ieee754.html.

2. Юровицкий В.М. IEEE754-тика угрожает человечеству. [Электронный ресурс].

Страница доступа: http://www.yur.ru/science/computer/IEEE754.htm

3.Аноприенко А.Я., Гранковский В.А., Иваница С.В. Пример Румпа в контексте традиционных, интервальных и постбинарных вычислений // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП-2011). Выпуск 9 (179):

Донецк: ДонНТУ, 2011. С. 324–343.

4.Аноприенко А.Я. Обобщенный кодо-логический базис в вычислительном моделировании и представлении знаний: эволюция идеи и перспективы развития // Научные труды Донецкого национального технического университета. Серия «Информатика, кибернетика и вычислительная техника» (ИКВТ-2005) выпуск 93. —

Донецк: ДонНТУ, 2005. — C. 289-316.

5.Moore R.E. Interval analysis. Eiiglewood Cliffs / R.E. Moore — N.J.:Prentic-e-llall,

1966.

6.Аноприенко А.Я., Иваница С.В. Интервальные вычисления и перспективы их развития в контексте кодо-логической эволюции // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП-2010). Выпуск 8 (168):

Донецк: ДонНТУ, 2010. С. 150–160.

7.Аноприенко А.Я., Иваница С.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли- Боруэйна-Плаффа // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ- 2010). Выпуск 11 (164). — Донецк: ДонНТУ, 2010. С. 19-23.

8.Суворова Е., Шейнин Ю. Проектирование цифровых систем на VHDL. —

СПб.: BHV, 2003. — С. 576.

9.Аноприенко А.Я. Тетралогика и тетракоды. / В кн. «Сборник трудов факультета вычислительной техники и информатики». Вып.1. Донецк, ДонГТУ, 1996.

10.Бесплатные программы SoftElectro. Программа IEEE754 — конвертор чисел формата IEEE754 c абсолютной точностью представления результата. Страница доступа: http://www.softelectro.ru/program.html.

11. Аноприенко А.Я. Археомоделирование: Модели и инструменты

докомпьютерной эпохи. — Донецек: УНИТЕХ, 2007. – 318 с.  

12. Аноприенко А.Я., Иваница С.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли- Боруэйна-Плаффа // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ- 2010). Выпуск 11 (164). – Донецк: ДонНТУ, 2010. С. 19-23.