Аноприенко А.Я., Коноплева А.П., 

 

Короткая аннотация. The history of cellular automaton is described. Alternative kinds of logic and codes and their application for the simulation of cellular automates are introduced. For automatons based on hypercodes and hyperlogic is proposed the term postbinarycellular automaton.

 

Клеточные автоматы (КА) на сегодняшний день являются одним из наиболее перспективных направлений моделирования. КА широко применяются для моделирования систем, для которых существенным является пространственное взаимодействие между элементами системы. Они используются для изучения общих феноменологических аспектов окружающего мира, включая коммуникации, вычисления, конструирование, рост, репродукцию, конкуренцию и эволюцию, также с помощью КА возможно моделирование не только феноменологических аспектов, но и самих законов физики, биологии и других наук.

 

В данной работе авторами предлагается метод моделирования КА на основе логики гиперкодов. Появление самой концепции гиперкодов было обусловлено относительной ограниченностью возможностей современных бинарных кодов на фоне сложности и неоднозначности реального мира. Постбинарные клеточные автоматы (ПКА) – это вид КА, в котором исходные комбинации задаются с помощью гиперкодов, а при задании состояний клеток и локальных зависимостей используются элементы гиперлогики.

 

Из истории КА

 

Клеточные автоматы – дискретные динамические системы, поведение которых полностью определяется в терминах локальных зависимостей. КА являются своего рода математическими идеализациями физической системы, в которой время и пространство дискретны, а физические величины принимают конечное множество значений [5]. Основными компонентами КА являются: дискретное пространство, дискретное время, локальные зависимости, правила (рецепты).

 

Теория КА обязана своим появлением двум ученым: Джону фон Нейману и Конраду Цузе. В работе Конрада Цузе «Вычислительное пространство» основная идея заключается в том, что Вселенная является огромным функционирующим КА ("cellular automation" (CA)). Особый интерес Цузе вызывало применение КА к задачам численного моделирования в механике и проблемам физики.

 

Однако, работа не получила столь широкого признания научных кругов, как работа Джона фон Неймана и Станислава Улама в области самовоспроизводящихся структур. Итогом многолетних трудов ученых стала книга Артура Беркса (1957 г.) «Клеточныеавтоматы» иразработанная модель самовоспроизведения на 300 000 ячеек, каждая ячейка которого включала 29 состояний. Именно это направление теории КА стало развиваться.

 

Следующей тенденцией развития КА стало стремление исследователей упростить сложный КА фон Неймана. Здесь широко известны работы Эдгара Кодда (1968), Эдвина Роджера Бэнкса,

 

Кристофера Лэнгтона (1984), H.H. Chou, J. Reggia (1993), Byl (1999) и др. исследователей, результатами работы которых стало появления множества КА с количеством состояний от 8 до 64 [6].

 

Важный вклад в развитие КА внесли ученые: Мартин Гарднер и Джон Хортон Конуэй. Известнейшая их работа игра «Жизнь» (1970) стала широко даже за пределами научных кругов [6].

 

В 1990 году вышла в переводе на русский язык книга «Машины клеточных автоматов» американских ученых из Массачусетского технологического института Тома Тоффоли и Нормана Марголуса, в которой систематично изложены основные достижения в области КА. Авторы описывают машину КА САМ-6, которая была создана в Массачусетском технологическом институте на основе языка FORTH. Машина работала на базе IBM-РС с памятью 256 К. С ее помощью можно было моделировать сложные модели физических процессов в газах и твердых телах. Также важное место отведено фундаментальным свойствам КА: параллельности и локальности [7].

 

Фундаментальные исследования в области КА были проведены Стивеном Вольфрамом. В 2002 году выходит большой труд ученого «Новый тип науки», объемом 1200 страниц, который посвящен КА.

 

Вольфрам делает акцент на возможности использования КА в качестве математических моделей физических, биологических и вычислительных систем благодаря простоте конструкции, возможности точного математического анализа и способности к сложномуповедению [5].

 

С момента появления теории КА интерес к этой проблеме возрастает. Исследования в этой области проводятся по всему миру учеными разных отраслей науки: в химии, физике, математике, биологии, экологии, социологии, криптографии, философии, компьютерной инженерии и нейронных сетях.

 

Классификация КА

 

Из современных классификаций КА наиболее известна классификация Вольфрама, основанная на анализе возможной сложности поведения КА. Положительным моментов классификации Вольфрама является осмысленность получаемых групп, которые характеризуют возможности по распространению и обработке информации КА. Но у этого подхода есть и отрицательные моменты – сложность определения класса для большинства КА.

 

Кроме возможной сложности поведения КА есть и другие признаки, по которым можно систематизировать КА. Предлагаемая ниже классификация базируется на принципе варьирования таких параметров КА, как состояние элементов, геометрия КА, тип соседства, локальные правила, способы организации автомата по времени.

 

Некоторые типы КА получаются путем совмещения различных вариантных параметров. Приведенная схема классификации сложна для восприятия, однако наиболее полно и точно отображает взаимосвязи различных параметров КА и их влияние на работуКА.

 

По пространственным характеристикам КА делятся на одномерные и многомерные в зависимости от количества пространственных координат сетки автомата. Одномерным является класс элементарных КА, наиболее полно изученный и описанный Стивеном Вольфрамом. Элементарный КА – одномерный массив, состоящий из конечных автоматов, каждый из которых может находиться в двух состояниях: 0 или 1, – и изменять свое состояние в дискретный момент времени в зависимости от своего состояния и состояния двух ближайших соседей (слева и справа). Все клетки обновляют состояния одновременно.

 

На практике из многомерных КА используются двумерные и реже трехмерные.

 

Из геометрических характеристик очень условно выделены окрестность и изометрия. Окрестность, которая состоит из клеток, имеющих общую вершину с данной, называется окрестностью Мура. Окрестность, которая состоит из клеток, имеющих общую сторону с данной, называется окрестностью фон Неймана.

 

Окрестность и изометрия взаимосвязаны и зависят также от временных характеристик (рисунок 2). В зависимости от того меняется ли геометрия автомата во времени, КА делятся на динамичные и статичные.

 

Изометрической характеристике присуще большое разнообразие различных вариантов. На рисунке 2 приведено для примера лишь малое количество видов изометрий (статичные: квадратная, треугольная, гексагональная; динамичные: Вольфрама, «Кирпичная стена», «Триумфатор», «Q-Bert», Марголуса).

 

По временным характеристикам КА подразделяются на синхронные, асинхронные, статичные и динамичные (о последних двух было сказано выше). В синхронных КА переход в новое состояние для всех клеток осуществляется одновременно по сигналу глобального таймера. В асинхронных КА клетки переходят в новое состояние в случайном порядке.

 

По способу формирования законов-рецептов КА данной классификацией выделяются детерминированные (последующее состояние ячейки однозначно определяется состоянием этой ячейки и ее ближайших соседей в предыдущий момент времени), вероятностные (состояния ячеек в последующий момент времени определяются на основе некоторых вероятностей), обобщающие (правила зависят только от общего числа значений соседних ячеек). По признаку однородности КА делятся на однородные и неоднородные. В однородных КА локальные функции переходов и индексы соседства одинаковы для каждой клетки. В неоднородных КА клетки могут иметь различные функции перехода или различные индексы соседства. Таким образом, в формировании этого признака участвуют два параметра: принцип формирования законов-рецептов и способ организации окрестности.

 

По типу состояний КА делятся на полигенные, элементы которого содержат различное множество возможных состояний En в разные моменты времени. На практике используются ячейки с эквивалентными состояниями в каждый момент времени – линейный КА. К линейным КА относятся бинарные (ячейке присущи состояния 0, 1), цветные (от двух до 224 состояний), вещественные (состояние ячеек описывается набором вещественных переменных), КА с памятью (добавляются свойства памяти к ячейке xi из ее собственной истории), КА без памяти (традиционные КА), КА на базе гиперлогики [1].

 

Постбинарные КА

 

Появление концепции гиперкодов было обусловлено относительной ограниченностью возможностей современных бинарных кодов на фоне сложности и неоднозначности реального мира. В работе [8], например, идея гиперлогики и гиперкодов излагается, как одно из наиболее перспективных направлений развития алгоритмического базиса вычислительного моделирования.

 

Существует много разновидностей КА. В данной работе рассматривается модифицированный клеточный автомат, в котором исходные комбинации задаются с помощью гиперкодов, а при задании состояний клеток и локальных зависимостей используются элементы гиперлогики. Для данной и подобных ей модификаций КА предлагается использовать обобщающее название постбинарные клеточные автоматы(ПКА).

 

Ранее в ряде публикаций [1-4] авторами были достаточно детально описаны варианты реализации ПКА. При этом предполагалось, что основное отличие от традиционных реализаций заключается в том, что входные значения ПКА задаются набором из двух гиперкодовых переменных Х и У, хранящих значения координат множества клеток первой генерации КА.

 

Примеры постбинарных КА

 

К настоящему времени реализованы варианты программ моделирования ПКА в среде Adobe Flash на языке Action Script и в среде Visual Studio 2008 на языках C++ и С#, интерфейсы которых представлены на рисунках 1 и 2 соответственно.

 

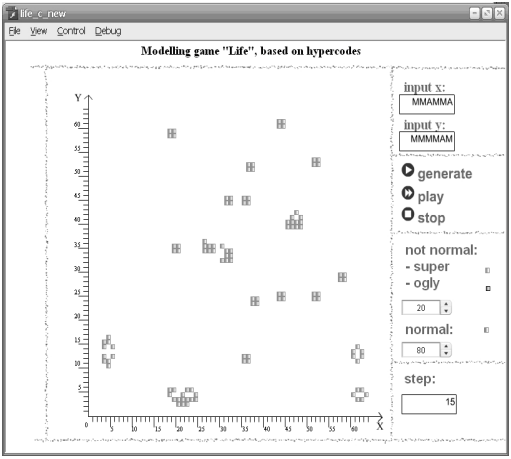
Рис.1. Интерфейс приложения для моделирования ПКА в среде Adobe Flash

 

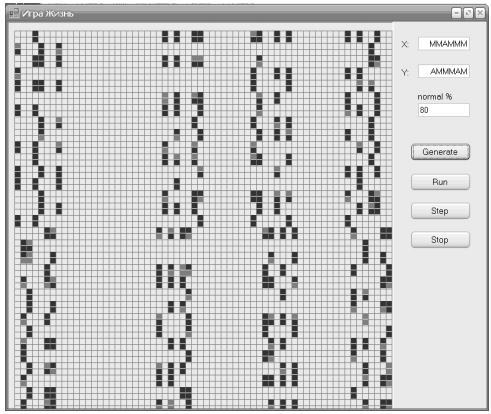
Рис. 2. Интерфейс приложения для моделирование ПКА на языке С++

 

На рис.1 приведен пример начальной генерации клеток. Диапазон значений задан двумя координатами в формате гиперкода Х=ММAММA и У=МMММAМ. При этом пользователем выбрано 80% нормальных клеток и 20% анормальных (т. е. слабых и сильных).

 

Задание начальной конфигурации клеток таким способом – удобный, быстрый и компактный метод. Кроме того, он позволяет генерировать квазислучайные комбинации множества точек в случае, если хотя бы в одном разряде одного из гиперкодов, присутствует вероятностное значение А.

 

Еще одним пример моделирования ПКА – ПКА с использование топологических масок. Предлагается моделирование ПКА с использованием топологических масок минимум двумя различными способами. При помощи одноразрядных и многоразрядных масок. Для первого метода следует рассмотреть несколько вариантов реализации.

 

1) Маска задается только для начальной генерации организмов. Это может выглядеть таким образом. Пользователь посредством интерфейса программы выбирает маску и размещает ее на поле. Запускает процесс моделирования и следит за развитием событий на поле. В этом случае организмы будут развиваться на всей территории без учета маски, то есть, ограничения территориальной маски действительны только на начальном этапе при задании первого поколения клеток.

 

Например, если в качестве таких масок использовать контуры 6 материков, с заданием на каждом континенте своих локальных законов, то можно получить наглядную модель развития определенных популяций организмов на всей планете. В качестве подобных масок могут быть использованы как более мелкие, так и более крупные ареалы в зависимости от целей моделирования.

 

На рис. 3 приведен пример задания первой генерации клеток при помощи топологической маски. В качестве топологической маски взята контурная карта Франции. Координаты Х=МММ0ММ, У=МАММММ. Процентное соотношение нормальных и ненормальных клеток – 80% и 20% соответственно.

 

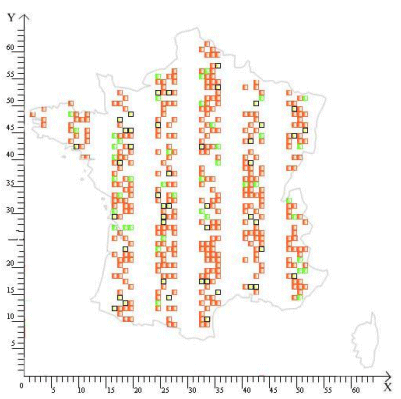
Рис. 3. Вариант задания топологической маски для начальной генерации клеток

 

Маска может быть и ограничивающей. То есть, внутри нее не могут быть размещены клетки, а все действия происходят за ее границами.

 

2) Маска задается и для начальной генерации, и для последующего развития организмов. Принцип наложения маски в этом случае аналогичен предыдущему, но начиная со второго шага будет контролироваться граница распространения клеток на поле.

 

Многоразрядные топологические маски могут носить одновременно несколько функций:

 

–ограничение главного диапазона, в котором размещены клетки всех видов;

 

–ограничение диапазонов, в которых будут действовать те или иные законы;

 

–ограничение ареалов для каждого вида клеток.

 

Каждая из функций должна быть обозначена своим цветом.

 

Этот вариант в настоящее время находится на этапе разработки. Он обеспечит пользователя более полным инструментарием для работы с гиперкодами.

 

Выводы

 

Основные результаты работы на данном этапе следующие.

 

- ряд приложений для ПКА с анализом их производительности и быстродействия [1-4];

 

-классификация всего множества известных КА, базирующаяся на принципе варьирования таких параметров КА, как состояние элементов, геометрия КА, тип соседства, локальные правила, способы организации автомата по времени [4];

 

-оценка производительности и быстродействия приложений для ПКА;

 

-предложены новые направления в работе с ПКА (в том числе ПКА с применением топологических масок);

 

-рассмотрены базовые концепции, положенные в основу теории КА.

 

Литература

 

1. Аноприенко А.Я., Коноплева А.П. Опыт применения гиперкодов в моделировании клеточных автоматов // Научные труды Донецкого национального технического университета. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" (МАП-2007). Выпуск 6 (127): Донецк:

 

ДонНТУ, 2007. С. 220-227.

 

2.Аноприенко А.Я., Коноплева А.П. Развитие идеи применения гиперкодов в моделировании клеточных автоматов // Научные труды Донецкого национального технического университета. Серия: Информатика, кибернетика и вычислительная техника (ИКВТ-2008) выпуск 93:- Донецк:ДонНТУ, 2008. C. 289-316.

 

3.Аноприенко А.Я., Коноплева А.П., Василенко А..Ю. Оценка производительности при моделировании постбинарных клеточных автоматов и способы ее повышения // Научные труды Донецкого национального технического университета. Серия: Информатика, кибернетика и вычислительная техника (ИКВТ- 2009) выпуск 147:- Донецк:ДонНТУ, 2009. C. 96-104.

 

4. Аноприенко А. Я., Коноплева А. П. Клеточные автоматы в историческом контексте и их классификация // Збірка матеріалів п’ятої міжнародної науково- технічної конференції студентів, аспірантів та молодих науковців 2009 р.. Серія «Інформатика та комп’ютерні технології» (ІКТ-2009). – Донецьк: ДонНТУ. – 2009. –

 

С.635-640.

 

5.Wolfram S. A New Kind of Science // http://www.wolframscience.com/nksonline/toc.html

 

6. Joel L. Schiff Cellular automata. A Discrete View of the World. // A John Wiley&Sons inc, Publication. Universityof Auckland. – 2008.– 279 p.

 

7.Тоффоли Т., Марголус Н. Машины клеточных автоматов // Издательство

 

«Мир», Москва, 1991. – 280 с.

 

8.Аноприенко А. Я. Эволюция алгоритмического базиса вычислительного моделирования и сложность реального мира // Научные труды Донецкого национального технического университета. Выпуск 52. Серия “Проблемы моделирования и автоматизации проектирования динамических систем” (МАП-2002).

 

–Донецк:ДонНТУ. – 2002. – С. 6-9.