| Проблемимоделювання та автоматизаціїпроектування |
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ПОСТБИНАРНОГО КОДИРОВАНИЯ ИНТЕРВАЛОВ
А.Я. Аноприенко, С.В. Иваница, E.В.Бурлака
Донецкий национальный технический университет
Представлена программная реализация извлечения из тетракода как полного набора двоичных и десятичных значений (преобразование тетракод? двоичное/десятичное число), так и значений границ интервала с оценкой их предельных колебаний(преобразование тетракод? интервал).
Введение
В настоящее время наблюдается стремительное увеличение объемов
исложности компьютерных вычислений, приводящее в свою очередь к возрастанию потребности контроля достоверности и точности вычислительных процессов. Возникающие при этом различного рода ошибки (например, связанные с неконтролируемым округлением чисел при использовании форматов с плавающей запятой [1]) часто незаметны, однако они существенно искажают результат и, в конечном счете, оказываются причинами ряда вычислительных катастроф [2]. Анализ подобных ситуаций позволяет предположить, что возможности классической двоичной логики на сегодняшний день исчерпаны, и при дальнейшем возрастании сложности вычислений использование двоичных компьютерных систем не гарантирует получения достоверных результатов. Этот факт может послужить началом пересмотра логики современных ЭВМ в рамках перехода к расширенному кодо-логическому базису[3, 4].
Рассмотрение расширенного двумерного логического пространства в [5] привело к появлению новых логических состояний, что позволило значительно расширитьвозможности формализованной логической оценки различных нюансов реальных процессов и ситуаций. На основе такого набора логических значений были введены в рассмотрение логические системы LN различных N порядков (гиперлогики), среди которых особый интерес вызывает логика четвертого порядка — тетралогика L4 ={0, 1, A,M} — представленная одним из многих вариантов набора четырех (из 17 возможных) логических значений. В работе [6] введено понятие тетракода C4 = {0, 1, A, M}, как системы кодирования количественной информации, построенной на основе тетралогики
Каждое значение тетракода (тетрит [7]) кодирует соответствующее состояние тетралогики: 0 — ложь (логический 0); 1 — истина (логическая1); А — неопределенность (ненаступление событий «истина» и «ложь»); М — множественность (обоюдное наступление событий «истина» и «ложь»). Рассматривая тетракод в качестве носителя количественной информации, можно высказать следующие предположения:
*тетриты 0 и 1 сводятся к битам 0 и 1 соответственно, так как они кодируют аналогичные логические состояния;
*тетрит М сводится к битам 0 и 1 одновременно, поэтому представим мдвумя точками на числовой оси;
*тетрит А сводится к битам 0 или 1 (в момент сведения его
значение неизвестно), поэтому представим одной из двух возможныхточек начисловой оси.
На основании данных предположений в [8] рассмотрены особенности представления (позиционирования на числовой оси) границ вещественных интервалов [9] одним значением тетракода. Приведены особенности представления диапазонов «плавающих» границ (т. е. ширины их предельных колебаний), предполагающих наличие совокупностей тетритов М и А в младших разрядахтетракода.
В данной работе рассматривается вариант применения тетракодов для получения множества значений на вещественной числовой оси, и, как следствие, сведение тетракода к крайним значениям этого множества для представленияинтервальныхчисел.
Целью данной работы является программная реализация процесса сведения тетракода к набору числовых значений, выраженных как множеством всех представимых данным тетракодом чисел, так и парой чисел, являющихся «скользящими» границами интервала. Для представления результатов такого преобразования были разработаны две аналогичные программные реализации «Перевод тетракода Т [0:31] {0,1,M,A} в 2/10 форматы чисел» в средах Adobe Flash CS4 (язык ActionScript, версия 3.0) и MS Visual Studio 2010 (язык С#,версия 4.0).
Особенности представления интервальныхчисел с помощью тетракода
Для получения численных значений при декодировании тетракода необходимопридерживаться следующихположений: поскольку один тетрит сводится к одному биту, то n-разрядный тетракод декодируетсяв набор n-разрядных двоичныхчисел; количество двоичных чисел в сведенном из тетракода наборе равно 2m, где m — количествотетритов М в тетракоде; наличие тетритов М в тетракоде позволяет рассматривать его как тетракод, сводящийсяк значениямграниц интервальногочисла.Последнее положение при декодировании тетракода требует более детального рассмотрения. При сведении значений тетритов ti (i — позиция тетрита в n-разрядном тетракоде, n–1? i? 0) тетракода к интервалу можно прибегнуть к предложенным в [10] унарным функциям тетралогики
(табл. 1): MIN_A (MAX_A) — минимизация (максимизация) неопределенности; MIN_М (MAX_М) — минимизация (максимизация) множественности.
Таблица 1.Функции минимизации и максимизации длятетритов А и М
| Унарная | Значение тетрита t | |||||
| функция | 0 | 1 | А | М | ||
| MIN_М(t) | 0 | 1 | А | 0 | ||
| MAX_М(t) | 0 | 1 | А | 1 | ||
| MIN_A(t) | 0 | 1 | 0 | М | ||
| MAX_A(t) | 0 | 1 | 1 | М | ||
Используя сочетания приведенных в таблице функций, можно все значения тетритов А и М привести к значениям 0 и 1. Тетракод, состоящий из тетритов 0 и 1, фактически является двоичным числом — значением интервальной границы. При сведении n-разрядного тетракода к значениям интервальных границ предлагается использовать следующие четыре сочетания:
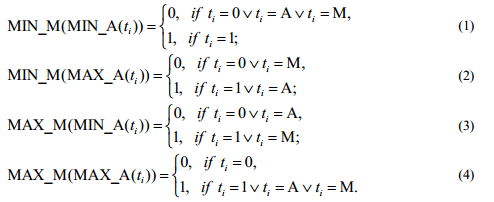
Таким образом, в качестве оценки предельных колебаний интервальных границ рассматриваются случаи получения их значений для интервалов, имеющих максимальную и минимальную ширину (под шириной интервала понимается диапазон принадлежащих данному интервалу значений, т.е. расстояние между его границами). Такая оценка предельных колебаний позволяет зафиксировать области, в которые гарантированно попадут границы извлеченного из тетракода интервала, поскольку при декодировании тетрита в интервал поле значений А сводится к случайному набору двоичных чисел. При этом корректное сведение тетракода к интервалу возможно лишь в том случае, если в исходном тетракоде тетриты А и М представлены группами, причем группа тетритов Адолжна занимать младшие разрядытетракода.
Структура программы декодирования тетракода
На рис. 1, 2 представлены два варианта программы, которая позволяет декодировать 32-разрядный тетракод с учетом описанных выше преобразований.
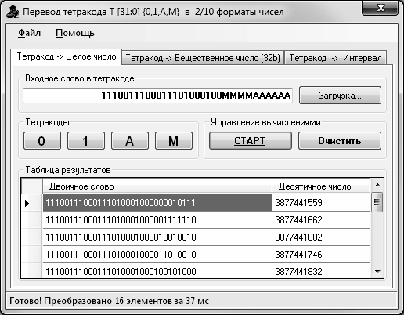
Рисунок 1 -Вариант программы, реализованной на языке С# (результат работы режима «Тетракод ? Целое число»)
Программа позволяет выполнить преобразование тетракодов в двоичные и десятичные наборы чисел. Исходный тетракод может быть «целочисленным» (сводиться к двоичным 32-разрядным целым беззнаковым числам) либо «вещественным» (сводиться к двоичным 32- разряднымчислам с плавающей запятой).
Программа имеет 4 режима работы в которых выполняются следующие преобразования:
1)Тетракод - Целое число: преобразование «целочисленного» тетракодав набор целых 32-разрядныхчисел(рис. 1).
2)Тетракод - Целочисленный интервал: сведение тетракода к паре
32-разрядныхцелых чисел,являющихсяграницами интервала.
3)Тетракод - Вещественное число: преобразование тетракода в наборвещественных 32-разрядныхчисел.
4)Тетракод - Вещественный интервал: сведение тетракода к паре
32-разрядных вещественных чисел, являющихся границами интервала(рис. 2).

Рисунок 2 - Вариант программы, реализованной на языке ActionScript (результат работы режима «Тетракод - Вещественный интервал»)
Программа имеет «интеллектуальный» механизм ввода значений, обеспечивающий «комфортный» ввод данных (ввод данных с клавиатуры ис экрана, возврат на предыдущий шаг ввода, очистка поля, и др.) и не позволяющей работать с некорректно введенной информацией (блокировка работы при событиях «введен не тетракод» для всех режимов и«некорректное размещение тетритов А и М в тетракоде» для режимов 2и 4). В нижней части окна программы отображается сопроводительная информация, которая включает следующие параметры: время выполнения преобразования тетракода и количество полученных при этом элементов (режимы 1 и 3); середина, ширина и «собранные» границы интервала (режимы 2 и 4). Результирующий набор полученных значений представлен в двоичныхи десятичныхчислах. Впрограмме предусмотрен ввод предустановленных значений тетракода (рис.2, поле «Выбор примеров»), а также загрузка из файла заранее подготовленных значений (рис. 1, кнопка «Загрузка…»). Имеется мультиязычная поддержка (русский, украинский и английский языки) интерфейсаи справочных материалов. Программа занимает около 250 КБ (flash-приложение) и 60 КБ (C#- приложение) дискового пространства. Вариант программы на flash отличается ярким динамическим интерфейсом, и изначально планировался дляиспользованияв виде веб-приложения.
Примеры декодирования тетракода
Рассмотрим декодирование тетракода на примере работы программы в 3-м и 4-м режимах. Значения тетритов исходного тетракода Т представленына рис. 3.

Рисунок 3 - Поле ввода вещественноготетракода flash-приложения (элементы checkbox определяют доступность полей к вводузначений)
Результаты работы программы в режиме 3 (сведение тетракода к наборувещественныхчисел) представлены на рис. 4.

Рисунок 4 - Результат сведениятетракодак набору вещественныхчисел
За 16 мс программа выполнила сведение тетракода Т к набору из 28 = 128 вещественных чисел (в тетракоде 8 тетритов М). При этом тетриты М в своей совокупности обеспечили полный перебор двоичных значений, а тетриты А в каждом числе из набора случайным образом свелись к нулевым или единичным битам. Повторные запуски программы приведут к получению различных по содержанию наборов чисел, поскольку тетриты А каждый раз будут заполняться случайными двоичными значениями.
В 4-м режиме работы программы (сведение тетракода к вещественному интервалу) возможны модификации получения результата (см. рис. 2): получение диапазонов колебаний границ («минимальная ширина интервала», «максимальная ширина интервала») и получение интервала с учетом случайного замещения двоичными значениями тетритов А. При отсутствии тетритов А в тетракоде, программа будет возвращать одинаковые интервалы не зависимо от выбранной модификации режима.
На рис. 5 представлены результаты работы программы при сведении тетракода Т к интервальнымграницамв каждой модификации.

Рисунок 5 - Результат сведениятетракодак вещественному интервалу(а — получение «крайне широких»границ; б — получение «крайне узких» границ, в — получение «случайных» границ)
Модификацию «максимальная ширина» (рис. 5, а) можно трактовать следующим образом: определение минимального и максимального значения в декодированном из тетракода наборе чисел. Действительно, каков бы не был набор чисел (с учетом разрядов А), ни одно число не будет меньше левой и больше правой границ интервала «максимальной ширины», численные значения которых можно получить из тетракода T, используя соотношения (1) и (4) для левой и правой границы соответственно,т. е.
[MIN_M(MIN_A(T)); MAX_M(MAX_A(T))] — искомый интервал.
Применение данной модификации представляет собой интервальную оценку «сверху», т. е. позволяет оценить максимальный «захват» участка числовой оси сведеннымиз тетракодаинтервалом.
Модификация «минимальная ширина» (рис. 5,б) отображает «худшие» случаи относительно тетритов А при определении границ интервала. Границы интервала «минимальной ширины» из тетракода T можно получить, используя соотношения (2) и (3) для левой и правой границысоответственно,т. е.
[MIN_M(MAX_A(T)); MAX_M(MIN_A(T))]— искомый интервал.
Применение данной модификации представляет собой интервальную оценку «снизу», т. е. позволяет оценить минимальный «захват» участка числовой оси сведеннымиз тетракодаинтервалом.
Действительно, границы интервала (с учетом разрядов А), полученные при модификации «случайные границы» (рис. 5,в), никогда не будут меньше по модулю соответствующих границ интервала «минимальной ширины».Таким образом, границы сведенногоиз тетракода Т интервала при любом случайном наборе бит для разрядов А будут принадлежать следующим диапазонам:
[MIN_M(MIN_A(T)); MIN_M(MAX_A(T))]— длялевой границы; [MAX_M(MIN_A(T)); MAX_M(MAX_A(T))]— для правой границы.
Ширина этих диапазонов определяет пределы колебаний границ интервала, полученного при декодировании тетракода Т. Такой интервал может быть записан в виде
??MIN_M(MIN_A(T)); MIN_M(MAX_A(T))?; ?
? ? ? ???MAX_M(MIN_A(T));MAX_M(MAX_A(T))???
? ?MIN_M(Rnd_A(T)); MAX_M(Rnd_A(T))?,
где Rnd_A — функция, сводящая тетрит А к двоичным 0 или 1, которые выбираются случайным образом.
Заключение
В данной работе рассмотрен способ постбинарного кодирования интервалов путем сведения тетракода к значениям интревальных границ. Предложены способы интервального оценивания (оценки предельных колебаний) границ интервала с использованием функций алгебры тетралогики. Представлена программная реализация рассматриваемой задачи — программа декодирования тетракода, которая позволяет выполнять:
–преобразование тетракодав наборцелочисленных значений;
–преобразование тетракодав наборвещественныхчисел;
– декодирование тетракода в границы интервалов с проведением интревального оценивания«сверху»и «снизу».
Разработанный программный продукт является в своем роде уникальным и может служить в учебных целях для наглядной иллюстрации представления тетракодов в виде числовых (точечных) и интервальных (множественных) значений. В дальнейшем планируется размещение данной программы (варианта, реализованного с помощью flash-технологии) напортале моделированияДонНТУ [11].
Список литературы
1.Аноприенко А.Я., ИваницаС.В. Интервальные вычисления и перспективы их развития в контексте кодо-логической эволюции // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП-2010). Выпуск 8 (168):
Донецк:ДонНТУ, 2010.С.150–160.
2.Аноприенко А.Я. Расширенный кодо-логический базис компьютерного моделирования.Кафедра ЭВМДонГТУ.Электронныйресурс.Страницадоступа: http://cs.donntu.ru/~anoprien/Publ/1997/base97ex.html.
3.Аноприенко А. Я. Обобщенный кодо-логический базис в вычислительном моделировании и представлении знаний: эволюция идеи и перспективы развития // Научные труды ДонНТУ. Выпуск 93. Серия «Информатика, кибернетика и вычислительная техника»(ИКВТ– 2005).– Донецк:ДонНТУ,2005.С. 289-316.
4.Аноприенко А.Я., КухтинА.А. О некоторых возможностях расширения логического базиса информатики. / В кн. ”Тези доповiдей мiжнародноi науково- практичноi конференцii «Iнформатизацiя в умовах переходу до ринку»”, Киiв, 5-6
листопада 1992р., с. 30–32.
5.Аноприенко А.Я. Тетралогика и тетракоды. / В кн. «Сборник трудов факультета вычислительной техники и информатики». Вып. 1. Донецк, ДонГТУ, 1996,
с.32–43.
6.Иваница С.В., Аноприенко А.Я. Особенности реализации операций тетралогики // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ-2011). Выпуск
13(185).— Донецк:ДонНТУ, 2011.С. 134–140.
7.Аноприенко А.Я., ИваницаС.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли- Боруэйна-Плаффа // Научные труды Донецкого национального технического университета. «Информатика, кибернетика и вычислительная техника». — 2010. —
Вып.11(164).— С. 19–23.
8.Hansen E., Walster G.W. Global optimization using interval analysis. — New York: Marcel Dekker,2004.
9.Иваница С.В., Аноприенко А.Я. Особенности реализации операций тетралогики // Научные труды Донецкого национального технического университета. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ-2011). Выпуск
13(185).— Донецк:ДонНТУ, 2011.С. 134–140.
10.Портал моделирования ДонНТУ. Электронный ресурс. Страницадоступа: http://sim.donntu.ru.
Поступила в редакцию23.09.2011 р. Рецензент: к.т.н., доц.Зеленева И.Я.
О.Я.Анопрієнко, С.В. Іваниця,Є.В. Бурлака
Донецькийнаціональній технічнийуніверситет
Програмна реалізація постбінарного кодування інтервалів. Представлена програмна реалізація вилучення з тетракоду як повного набору двійкових і десяткових значень (перетворення тетракод ? двійкове/десяткове число), так і значень границь інтервалу з оцінкою їх граничних коливань(перетворення тетракод? інтервал).
Інтервал,програма, тетралогіка, тетракод
А.Anoprienko,S.Ivanitsa,Е.Burlaka
DonetskNational Technical University
Software implementation of coding postbinary intervals. Presented a software implementation, which extracts from tetraсodе a complete set of binary and decimal values (convert tetraсodе ? binary/decimal) and values of the limits of the interval with an estimate oftheirmarginalfluctuations (convert tetracode? interval).
Interval,program, tetralogic, tetracode.