РЕАЛИЗАЦИЯ ИНТЕРВАЛЬНЫХ ВЫЧИСЛЕНИЙ СРЕДСТВАМИ МАТЕМАТИЧЕСКОГО ПАКЕТА SCILAB С ИСПОЛЬЗОВАНИЕМ ИНТЕРВАЛЬНОГО РАСШИРЕНИЯ INT4SCI
А.Я. Аноприенко, С.В. Иваница Донецкий национальный технический университет
Представлено реалізацію інтервальних обчислень засобами математичного середовища SciLab з використанням пакета інтервального розширення Int4Sci на прикладі обчислення інтервальної функції. Позначено можливість обліку погрішності вхідних даних і перевірки коректності результатів обчислень.
Математический пакет Scilab — система компьютерной математики, созданная как европейский аналог Matlab'а. Особенностью Scilab'а является то, что это свободно распространяемый некоммерческий продукт с открытыми исходными кодами. Различные версии Scilab'а адаптированы как для Gnu/Linux и Windows 2000/XP/Vista, так и для других платформ [1]. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе такие компании как
Mandriva, INRIA и ENPC (Франция). Помимо того, что Scilab
содержит сотни математических функций, существует возможность добавления новых функций и расширений, написанных на различных языках программирования. Одним из таких расширений является пакет Int4Sci.
Пакет Int4Sci — интервальное расширение Scilab'а, развиваемое и свободно распространяемое группой французских разработчиков [2]. Int4Sci представляет собой дружественный к пользователю набор инструментов для реализации интервальных вычислений, и добавляет к базовому вычислительному программному обеспечению основные конструкции интервальных типов данных и прототипы функций, реализующих интервальные методы.
На данный момент пакет Int4Sci обладает совокупностью следующих функциональных возможностей:
–расширенная интервальная арифметика;
–элементарная оценка интервальных функций;
–вычисление характеристик интервалов;
–интервальные преобразования.
Рассмотрим практическое применение математического пакета Scilab в совокупности с его интервальным расширением Int4Sci. В
|
качестве примера, |
для функции f (x) =sin 2x cos x2 , график которой |
приведен на рис.1, вычислим точечное значение при x = 1. Поскольку в Scilab формат вывода вещественного числа по умолчанию равен восьми значащим цифрам, то получим значение функции f(1) = 0.4912955.
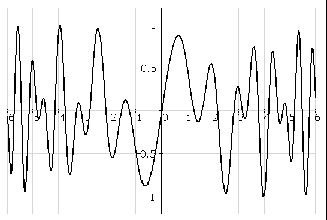
Рис. 1. График функции f(x)
Приведем число х к интервальному виду, причем наиболее приближенное к числу 1 в данном формате представления вещественных чисел, например х = [0.9999999, 1.0000001]. На рис.2
показано вычисление уже интервальной функции Fx =sin 2x cos x2 ,
возвращающей результирующий интервал [0.4912953, 0.4912957], который гарантирует точность первых 7-ми цифр результата. Очевидно, что число f(1) = 0.4912955 принадлежит полученному интервалу, и, кроме того, является его серединой. Однако такое «центральное попадание» результата в выходной (конечный) интервал возможно только при достаточном приближении границ входного (начального) интервала к исходным величинам.
Расширим границы входного интервала до значений х = [0.3, 1.7] и получим значение Fx = [–0.9685172, 0.9959527]. На рис. 3 показана область, ограниченная границами входного и выходного интервалов. При этом видно, что в результирующем интервале все значения в диапазоне от –0.18 до 0.9959527 гарантировано являются «пустыми». Такая ситуация обусловлена тем, что во-первых, в рамках интервального подхода операции (прежде всего арифметические) определяются таким образом, что результат соответствующей точной
операции обязательно лежит внутри вычисляемых границ результирующего интервала, и, во-вторых, возникающая при вычислении границ погрешность учитывается с помощью направленных округлений [3].
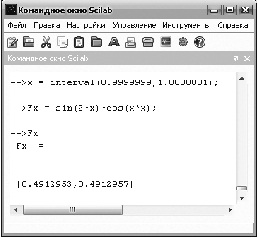
Рис. 2. Вычисление интервальной функции Fx
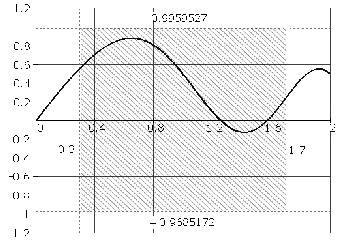
Рис. 3. Вычисление функции Fx при х = [0.3, 1.7]
Приведем функцию f(x) к функции от двух переменных f(x,у) таким образом, чтобы эти функции оставались эквивалентными:
f (x, y) =sin (x + y) cos xy,
т. е. f(x) = f(x,у), если x = у.
График функции f(x,у) представлен на рис. 4. Пусть, как и в предыдущем случае, х = [0.3, 1.7]. Выберем граничные значения
|
интервала у такими, чтобы выполнялось |
условие x у, |
например |
|
y = [0.9, 1.1]. |
|
|
|
|
|
Результаты |
вычисления |
значений |
интервальной |
функции |
|
Fxy =sin (x + y) cos xy в пакете Scilab: |
|
|
--> x = interval(0.3,1.7); --> y = interval(0.9,1.1); --> Fxy = sin(x+y)*cos(x*y) Fxy =
|-0.2947594,0.9637709|
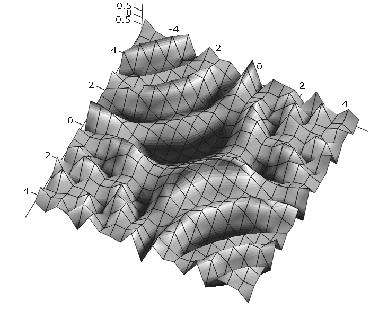
Рис. 4. График функции f(x,y)
Таким образом, Fx = [–0.2947594, 0.9637709]. Такой интервал дает более точное представление результата, чем полученные ранее значения в интервале Fx = [–0.9685172, 0.9959527] за счет более точного представления переменной y.
Выводы
Проблема математической корректности вычислений становится в настоящее время центральной. В последние годы для многих задач численного анализа были разработаны методы решения, дающие возможность автоматически проверять корректность результатов вычислений. Часто такие методы допускают использование компьютинга для автоматического доказательства существования и единственности решения численной задачи.
Приведенный иллюстративный пример вычисления интервальной функции в среде SciLab открывает одну из ряда возможностей
упрощения многих проблем, возникающих при решении прикладных задач стандартными (точечными) методами. Однако основной проблемой интервального анализа является корректное определение интервалов неопределенности при наличии различных источников неопределенности исходных данных. В этом плане представляется перспективной работа [4], в которой внутри интервала неопределенности выделяется как систематическая так и случайная составляющие.
Таким образом, приведенные результаты дают основание сделать заключение, что применение интервального анализа, реализуемого связкой программных пакетов SciLab-Int4Sci, к широкому спектру прикладных задач имеет большие перспективы.
Библиографический список
1.Scilab. The Free Platform for Numerical Computation http://www.scilab.org.
2.Int4Sci Toolbox: A Scilab Interface for Interval Analysis http://www- sop.inria.fr/coprin/logiciels/Int4Sci.
3.Hammer R., Hocks M., Kulisch U., Ratz D. Numerical toolbox for verified computing I: Basic numerical problems. — Berlin-Heidelberg: Springer, 1993.
4.Design of Experiments and Data Analysis: New Trends and Results, ANTAL, Moscow, 1993.



