Математические методы и организация планирования производства
Автор: L. V. Kantorovich
Автор перевода: Кулик Е.А.
Источник: Сайт «docs.google.com»
Автор: L. V. Kantorovich
Автор перевода: Кулик Е.А.
Источник: Сайт «docs.google.com»
Автор работы «Математические методы организации и планирования производства», профессор Л. В. Канторович, является выдающимся специалистом в области математики. Эта работа интересна с чисто математической точки зрения, поскольку она представляет собой оригинальный метод, выход за пределы классического математического анализа, для решения экстремальных задач. С другой стороны, эта работа также обеспечивает применение математических методов к вопросам организации производства, которая заслуживает серьезного внимания работников в различных отраслях промышленности.
Работа, которая представлена здесь, обсуждалась на заседании секции Математики Института математики и механики Ленинградского государственного университета и получила высокую оценку математиков. Кроме того, было созвано специальное совещание работников промышленности управления университетом, на котором обсуждались другие аспекты работы и ее практическое применение. Промышленные рабочие единодушно проявили большой интерес к работе и выразили желание увидеть ее опубликованной в ближайшем будущем.
Основная часть монографии воспроизводит содержание доклада и приводится в совещаниях, упомянутых выше. Она включает в себя представление математических задач и тех вопросов организации в области промышленности, строительства, транспорта и сельского хозяйства, которые ведут к разработке этих проблем. Экспозиция иллюстрирует несколько конкретных числовых примеров. Нехватка времени и то, что автор является математиком, не позволяют увеличить число этих примеров, связанных с промышленным производством. Мы считаем, что, несмотря на это, такие примеры будут очень полезны для читателя, ибо они доказывают обстоятельства, в которых математические методы применяются, а также эффективность их применения.
Три приложения к работе содержат изложение и основы процесса решения указанных экстремальных задач по методу автора.
Мы надеемся, что эта монография будет играть очень важную роль в развитии нашей социалистической промышленности.
Огромные задачи, изложенные в плане третьей пятилетки требует, чтобы мы достигли максимально возможной продуктивности на основе оптимального использования имеющихся резервов промышленности: материалы, рабочую силу и оборудование.
Есть два пути повышения эффективности работы магазина, предприятия или целой ветви промышленности. Один путь состоит в различных нововведениях в технологии, то есть, новое навесное оборудование для отдельных машин, изменение технологических процессов, а также открытие новых, лучших видов сырья. Другой способ, до сих пор намного меньше использовали, улучшение в организации планирования и производства. Здесь включены, например, такие вопросы, как распределение работы между отдельными машинами предприятия или одним из механизмов, правильное распределение заказов между предприятиями, правильное распределение различных видов сырья, топлива и других факторов. И четко упоминается в резолюции 18–го съезда партии. Там сказано, что "самое главное для достижения целей программы по росту производства в странах третьего пятилетнего плана является ... широкое развитие работы по пропаганде самых современных технологий и научной организации производства ". Таким образом, две линии подхода, указанных выше указано: а также внедрение самых современных технологий, роли научной организации подчеркивается.
В связи с решением задачи представлены в Институт математики и механики Ленинградского государственного университета в лаборатории фанерного треста, я обнаружил, что целый ряд проблем из самых разнообразных символов, связанных с научной организацией производства ( вопросы оптимального распределения работы машин и механизмов, минимизации отходов, оптимального использования сырья и местные материалы, топливо, транспорт и т.д.) приводят к формулировке одной группе математических задач (экстремальные задачи ). Эти проблемы напрямую не сопоставимы с проблемами, рассматриваемыми в математическом анализе. Более правильно было бы сказать, что они формально похожи, и даже оказаться формально очень просто, но процесс их решения, с которым сталкивается [т.е. математический анализ] практически полностью непригодным, так как она требует решения десятки тысяч или даже миллионов систем уравнений для заполнения.
Мне удалось найти сравнительно простой общий метод решения этой группы задач, которые применимы ко всем проблемам, которые я уже упоминал, и является достаточно простым и эффективным для их решения должны быть сделаны полностью достижимой в реальных условиях.
Я хочу еще раз подчеркнуть, что большая часть проблем, о которых я буду говорить, касающиеся организации и планирования производства, связаны именно с советской системой хозяйства, и в большинстве случаев не возникает в экономике капиталистического общества. Там выбор продукции определяется не по плану, а по интересам и прибыли отдельных капиталистов. Владелец предприятия выбирает для производства тех товаров, которые в данный момент имеют наиболее высокую цену, легче всего продается, и поэтому дают наибольшую прибыль. В качестве сырья используется не то, чего имеются огромные запасы в стране, но то, что предприниматель может купить наиболее дешево. Вопрос о том, максимальное использование оборудования не возникает, во всяком случае, большинство предприятий работают в половину мощности.
В СССР ситуация иная. Все подчинено не интересы и достоинство отдельного предприятия, но с задачей выполнения государственного плана. Основной задачей предприятия является выполнение и перевыполнение плана, который является частью общего государственного плана. Более того, это означает не только выполнение плана в совокупном выражении (т.е. общей стоимости продукции, общий тоннаж, и так далее), но определенные выполнение плана по всем видам продукции, то есть выполнение плана ассортимента ( выполнение плана по каждому виду продукции, полнота отдельных элементов производства, и так далее).
Эта функция, необходимость выполнения как общего плана, и все ее составные части, имеет важное значение для нас, так как в условиях задач, связанных с обеспечением максимальной мощности мы должны рассмотреть вопрос о составе и полноте чрезвычайно важным дополнительным условиям. Кроме того, чрезвычайно важным является использование материалов, не выбрал в некоторых априорного, но те, которые действительно доступны, в частности, местных материалов и использования материалов в соответствии с объемом их производства в данном регионе. Следует отметить, что наши методы позволяют решить проблемы, связанные именно с этим реальным условиям и ситуациям.
Перейдем теперь к рассмотрению различных практических вопросов организации и планирования производства и выясним, математических задач, к которым они приводят.
Для того чтобы проиллюстрировать характер проблем, которые мы имеем в виду, я приведу один очень простой пример, который не требует специальных методов решения, так как ясно само по себе. Этот пример поможет уточнить постановку задачи.
Пример 1. Фрезерные работы по производству частей изделий из металла можно сделать на разных машинах: фрезерные станки, револьверные станки более продвинутый тип и автоматической револьверный станок. Для точности я должен рассмотреть следующие проблемы. Есть три фрезерных станка, три револьверные станка, и один токарный автомат башни. Этот пункт будет опущен, я буду считать чрезвычайно простой случай, состоящий из двух частей.
Выход каждой части выглядит следующим образом. Во время рабочего дня можно оказаться на фрезерном станке, 10 части первой и 20 второй, на револьверный станок, 20 части первой и 30 второй, а с автоматической револьверный станок, 30 первого и 80 второго. Таким образом, если мы рассматриваем все машины (по три на фрезерных станках и револьверные станки, и один автомат), мы можем, если мы хотим превратить в день 30 + 60 + 30 первой части на каждый тип машины, соответственно, или в общей сложности 120 частей на всех машинах. Из второй части, мы можем оказаться 60 + 90 + 80. (См. Таблицу 1).
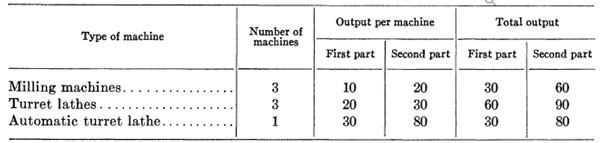
Таблица 1 – Производительность машин. Две части
Теперь мы должны решить следующие задачи: работа должна быть разделена таким образом, чтобы загрузить рабочий день эти машины таким образом, чтобы достичь максимальной мощности, и в то же время важно не только для получения максимального количество деталей, но, чтобы найти метод максимального выхода готовых изделий, в данном случае состоит из двух частей. Таким образом, мы должны разделить время работы каждой машины таким образом, чтобы получить максимальное количество готовых изделий.
Если бы не попытка получить максимум, но только для достижения полноты, то мы могли бы производить обе части на каждой машине в равных количествах. Для этого достаточно разделить рабочий день каждой машины таким образом, что он производит такое же количество каждой части. Тогда получается, что фрезерный машинном может производить 20 части первой и 20 секунды. (На самом деле, на фрезерные станки производства 20 второй части составляет 10 первого). Револьверные станки могут производить 36 первых и 36 секунды; автоматический револьверный станок может производить 21 первых и 21 второй части, а общий объем производства всех машин будет 77–й и 77 второй части, или, другими словами, 77 полных пунктов. (См. Таблицу 2).
Найдем теперь, в данном примере, наиболее целесообразный метод работы. Мы рассмотрим различные коэффициенты. На фрезерном станке, одну единицу первой части равна двум второй, на револьверный станок, это соотношение составляет от 2 до 3, на автомате, от 3 до 8. Существуют различные причины для этого, одной из операций может потребовать то же время на каждой машине, другая операция может быть выполнена в пять раз быстрее, чем автомат на фрезерном станке, и так далее. Благодаря этим условиям, эти показатели отличаются для различных машин выпускать одинаковые части. Одна часть может быть оказалась относительно лучше на одной машине, другая часть на другой машине.
Рассмотрение этих соотношений сразу же приводит к решению. Это необходимо, чтобы оказаться в первой части, где он весьма успешно производятся (на револьверный станок), а вторая часть должна быть назначена автомат. Что касается фрезерных станков обеспокоены, производство Первая и вторая части должны быть частично разделить между собой таким образом, чтобы получить столько же первой и второй частей.
Если мы сделаем назначение в соответствии с этим методом, их число будет выглядеть следующим образом: на фрезерном станке будет 26 и 6; на револьверный станок только 60 первых, и ни один из secolnd, на автомате 80 второй, и ни одна из первых. Всего мы получим 86 первой части и 86 секунды. (Табл. 2).
Если такое перераспределение осуществляется, то мы получим эффект, который не очень велика, но все же заметным: увеличение объемов производства на 11 процентов. Кроме того, это возрастание в производство происходит без расходов угодно.
Эта проблема была решена так легко из элементарных соображений, потому что у нас было только три машины и две части. Практически, в большинстве случаев приходится иметь дело с более сложной ситуации, и найти решение просто здравый смысл вряд ли возможно. Это слишком много, чтобы надеяться, что обычный инженер, без расчета любого рода, будет происходить на лучшее решение. В табл. 2 представлено распределение обработки деталей из машины.

Таблица 2 – Распределение обработки деталей из машины
Для того, чтобы получить вид математической задачи, к которой ведет, я должен рассмотреть этот вопрос в более общем виде. Я буду вводить здесь несколько математических задач, связанных с вопросом о производстве элементов, состоящих из нескольких частей. Что касается всех других областях применения математических методов, которые я упоминал выше, оказывается, что математические задачи одни и те же в каждом конкретном случае, так что в других случаях это будет только мне нужно, чтобы указать, какие из эти проблемы представляют ситуацию.
Поэтому, давайте посмотрим на общий случай. У нас есть определенное число n машин и на них оказывается элементов, состоящий из m различных частей. Допустим, что если мы производим k–й части на i–й машины мы можем производить в день a(i, k) части. Эти приведенные данные. (Заметим, что если это невозможно, чтобы оказаться k–й части на i–й машины, то необходимо установить соответствующие a(i, k) = 0.
Теперь то, что нам нужно? Необходимо распределять работу принятия части среди машин таким образом, чтобы оказаться большое количество готовых изделий. Обозначим время h(i, k), время (выраженное как доля рабочего дня), что мы собираемся использовать i–й машины для производства производим k–й части. На этот раз неизвестно, необходимо определить его на основе условия получения максимальной отдачи. Для определения h(i, k) есть следующие условия. Первый час h(i, k)> 0, то есть, она не должна быть отрицательной. С практической точки зрения это условие совершенно очевидно, но следует отметить, поскольку математически она играет важную роль усложняет. Кроме того, при каждом фиксированном я сумма Sum( h(i, k))= 1, то есть, это условие означает, что i–я машина загружена на полный рабочий день. Кроме того, число k–я часть производства будет Zk = Sum(a(i,k)*h(i,k)), так как каждый продукт a(i,k)*h(i,k), дает количество k–й части производится на i–й машины. Если мы хотим получить готовых изделий, мы должны потребовать, чтобы все эти величины равны друг другу, то есть, Z1 = Z2 = ... = Zm. Общее значение этих цифр, z, которое определяет количество элементов, должно быть максимальным.