Назад в библиотеку

Периодические линии тренда в прогнозировании объемов продаж

Автор:Загинайло И.В., консультант компании «Экселент Консалтинг Груп», Одесса, Украина
Источник: Сайт о финансовом моделировании «cfin.ru»

Возможности классической методики прогнозирования могут быть существенно расширены, если выйти за рамки ограниченного набора типов линий тренда, предлагаемых «по умолчанию» в MS Excel.

Зачем это нужно? Затем, что выбор линии тренда может быть не просто формальным актом в математических вычислениях. Выделение трендов, коррелирующих с поведением реальных факторов, влияющих на прогнозируемую величину, повышает достоверность прогнозов, делает их более «прозрачными» для понимания. Данная статья показывает, как выбирать и использовать дополнительные типы линий тренда в рамках упомянутой методики.

В качестве примера будем использовать данные об объемах продаж Нижегородского мороженого (табл. 1)

Таблица 1 – Фактические объемы реализации продукции

№ п.п.МесяцОбъем продаж (руб.)№ п.п.МесяцОбъем продаж (руб.)
1июль8174,4013июль

8991,84
2август5078,3314август

5586,16
3сентябрь4507,2015сентябрь

4957,92
4октябрь2257,1916октябрь

2482,91
5ноябрь3400,6917ноябрь

3740,76
6декабрь2968,7118декабрь

3265,58
7январь2147,1419январь

2361,85
8февраль1325,5620февраль

1458,12
9март2290,9521март

2520,05
10апрель2953,3422апрель

3248,67
11май4216,2823май

4637,91
12июнь8227,56924июнь9050,3264

Полезно взглянуть также и на графическое отображение изменений объемов продаж, которое показано на рис. 1.

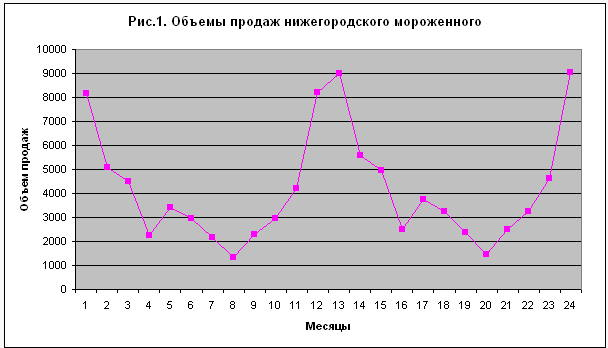
Объемы продаж нижегородского мороженого

Рисунок 1 – Объемы продаж нижегородского мороженого

Напомню поставленную предыдущими авторами задачу: составить прогноз продаж продукции на следующий год по месяцам.

Конечно, если бы автор нашел годовые графики среднемесячных температур в Нижнем Новгороде, данные о числе ненастных дней по месяцам, кривые заболеваемости ОРВИ (что происходило по октябрям в Н.Н., с чем коррелирует наблюдаемый спад продаж?), возможно, что–то еще, то наше прогнозирование пошло бы иным путем. Но в отсутствие этих данных мы можем констатировать лишь одно: налицо нечто, напоминающее периодическую функцию. А периодическая функция может быть представлена в виде суммы гармонических функций или, иначе говоря, рядом Фурье.

Итак, попробуем выделить из наблюдаемого ряда значений синусоидальный тренд с периодом колебания 12 месяцев:

Здесь Y12 – функция тренда, A12 — смещение синусоиды относительно нуля, B12 — амплитуда синусоиды, C12 имеет смысл начальной фазы колебания, индекс 12 указывает на выбранный нами период изменения функции. Эта функция будет отражать воздействие температурного (погодного) фактора на продажи мороженого.

Для того, чтобы MS Excel помогла нам сделать необходимые вычисления, понадобится активизировать (а, возможно, и доустановить) некоторые надстройки. Зайдите в меню «Сервис» и выберите команду «Надстройки…». В показанном списке надстроек установите флажки напротив «Analysis ToolPak — VBA», «Пакет анализа» и «Поиск решения». Нажмите ОК. Возможно, что MS Excel потребует установочный диск — приготовьте его заранее.

Теперь поручим MS Excel подобрать наилучшие значения A12, B12 и C12.

Итак, на чистом рабочем листе (назовем его «Шаг 1») в ячейки А3:А26 запишем номера месяцев наблюдения от 1 до 24, а в ячейки В3:В26 — наблюдаемые объемы продаж. Особенность надстройки «Поиск решения» состоит в том, что требуется задать затравочные значения A12, B12 и C12. Значение A12 должно быть близко к среднему значению объема продаж за год; в качестве затравочного значения выберем 4000 и занесем это число в ячейку Н3. B12 — это амплитуда искомой синусоиды, ее затравочное значение определим как «A12 минус минимальное значение объема продаж». Подойдет самая грубая оценка: 3000; занесем это число в ячейку I3. Судя по графику, C12 или начальная фаза приблизительно составляет – 1/4 периода, или – 3 месяца. Запишем – 3 в ячейку J3. В ячейку К3 поместим наш период: 12 (подбирать его мы не будем, но нам удобно, чтобы он фигурировал в этой ячейке). Наш следующий шаг: необходимо уравнение нашей синусоиды записать в виде формулы MS Excel. Для этого в ячейку D3 заносим: =$H$3+$I$3*SIN(2*ПИ()*(A3–$J$3)/$K$3) (все буквы, кроме «ПИ», латинские; ПИ() — это функция русифицированного MS Excel, которая возвращает константу 3,1415926…; в наборе формулы важно не ошибиться! ). Если после ввода формулы в ячейке D3 появится число 6598 (десятичные знаки опущены), то у вас все получилось, и можно автозаполнителем скопировать эту формулу в ячейки D4:D26. Теперь в ячейках Е3:Е26 вычислим отклонения нашей синусоиды от базовой линии прогноза: в Е3 запишем формулу: =B3–D3 , и скопируем ее автозаполнителем в указанный диапазон. В ячейках F3:F26 необходимо рассчитать квадраты отклонений, для чего в F3 запишем: =E3*E3 и скопируем эту формулу ниже автозаполнителем. В ячейке F27 подсчитаем сумму квадратов отклонений: =СУММ(F3:F26).

И вот наступает ответственный момент. Выделив ячейку F27 с подсчитанной суммой квадратов отклонений, в меню «Сервис» выбираем команду «Поиск решения…». В диалоговом окне в поле «Установить целевую ячейку» должно быть указано $F$27. В переключателе «равной» выбираем «минимальному значению», а в поле «Изменяя ячейки» указываем: $H$3:$J$3 . Скриншот этого диалога показан на рис. 2.

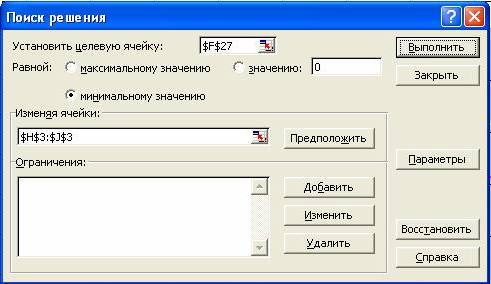
Настроенное окно диалога

Рисунок 2 – Настроенное окно диалога "Поиск решения"

Нажав кнопку «Выполнить», мы получаем в ячейках H3:J3 значения A12=4160, B12=2686 и C12=–2,03, наилучшим образом приближающие нашу синусоиду к базовой линии. Осталось в завершающем диалоге подтвердить сохранение найденного решения.

Полезно вычислить квадрат коэффициента корреляции (коэффициент детерминации R2) полученного тренда с базовым рядом; в ячейку G27 введем формулу: =КВПИРСОН(D3:D26;B3:B26) . У меня получилось 0,696669. Хорошо это или плохо? Насколько значим полученный коэффициент детерминации?

Для оценки значимости коэффициента детерминации воспользуемся t–критерием Стьюдента. Обычно требуется определить фактическое значение критерия

и сравнить его со значением t–критерия Стьюдента ta(k) с заданными доверительной вероятностью a и числом степеней свободы k=n–1, где n — число наблюдений. Если tr > ta(k), то величину коэффициента корреляции следует признать существенной. Мы поступим иначе: определим минимальное значение R2, при котором корреляцию можно считать существенной:

Запишем в ячейку Н27 число наблюдений базового ряда: 24. В ячейке I27 с помощью формулы =СТЬЮДРАСПОБР(0,05;H27–1) найдем коэффициент Стьюдента для доверительной вероятности 0,95 и числа степеней свободы 23 (равен 2,06855). В ячейке J27 вычислим квадрат коэффициента Стьюдента формулой =I27*I27. И в ячейке К27 получим минимальное существенное значение коэффициента детерминации с помощью формулы =J27/(H27–2+J27). Итак, оказывается, что с вероятностью 0,95 корреляция будет существенна, если R2 > 0,16284. Таким образом, корреляцию нашей линии тренда с базовой линией прогноза следует признать существенной.

На рис.3 показаны графики базовой линии прогноза, линии тренда и отклонений.

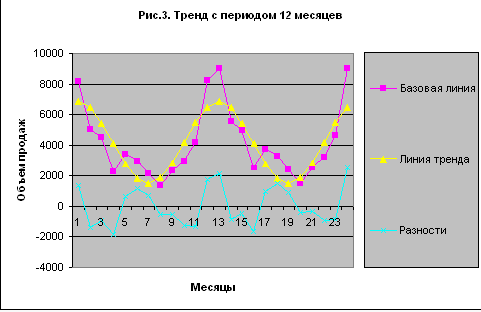
Тренд с периодом 12 месяцев

Рисунок 3 – Тренд с периодом 12 месяцев

Что можно сказать о поведении отклонений? Не прослеживается ли в них тоже периодичность, но уже с меньшим периодом — 6 месяцев? Есть ли факторы, которые могут с такой периодичностью воздействовать на продажи мороженого? На последний вопрос должны ответить маркетологи. Я же позволю себе пофантазировать… например, рождественские каникулы и летние отпуска, экзаменационные сессии у студентов, каникулы у школьников имеют полугодичные ритмы. Если люди, живущие в полугодичных ритмах, составляют существенную часть сегмента потребителей мороженого, то почему бы этим ритмам не проявиться в колебаниях спроса? Однако при серьезном подходе к прогнозированию я бы рекомендовал воздерживаться от фантазий и задавать побольше вопросов маркетологам. Но мы изучаем метод, и поэтому примем гипотезу о полугодичном периоде в тренде (а иначе что будет предметом нашего дальнейшего рассмотрения?).

Итак, запасайтесь терпением: нам будет необходимо проделать все то же самое, но для периода 6 месяцев: теперь мы отыщем линию тренда, т.е. подберем коэффициенты A6, B6 и C6. А вместо базовой линии прогноза мы будем работать с разностями, полученными в первом шаге (приближении). Дело пойдет быстрее, если Вы поступите следующим образом.

  1. Создайте копию листа «Шаг 1», переименуйте эту копию в «Шаг 2»;
  2. В ячейку В3 запишите формулу: ='Шаг 1'!E3 («Е» — латинское!) и автозаполнителем скопируйте ее в ячейки В4:В26; мы сейчас заменили исходный ряд наблюдений разностями, полученными на листе «Шаг 1»;
  3. В ячейке Н3 укажите затравочное значение для A6; подойдет ноль;
  4. В ячейке I3 укажите затравочное значение для B6; можно начать с 1000;
  5. В ячейке К3 укажите период: 6;
  6. В ячейке J3 укажите затравочное значение для C6; подойдет любое число в диапазоне от –3 до 3;
  7. Выделите ячейку F27 и выполните «Поиск решения».

Результатом будет A6=0,0127, B6=1449 и C6=–1,099; коэффициент детерминации
R2=0,66827 > 0,16284. Таким образом, эту корреляцию также следует признать существенной.

На рис.4 показаны графики базовой линии прогноза, суммы трендов 12 и 6 месяцев, отклонений суммы трендов от базовой линии.

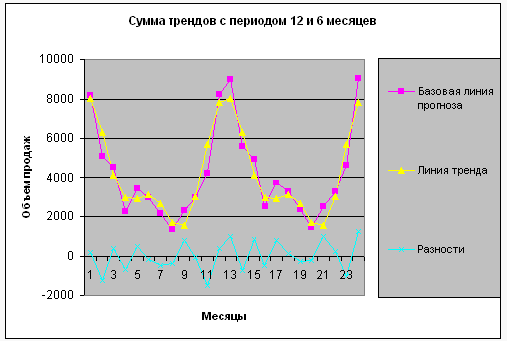
Сумма трендов с периодом 6 и 12 месяцев

Рисунок 4 – Сумма трендов с периодом 6 и 12 месяцев

Что теперь можно сказать об отклонениях? Во–первых, в них по–прежнему можно заметить периодичность. Причем с приблизительно одинаковой значимостью в них обнаруживаются колебания с периодами 3 и 4 месяца. Во–вторых, в них просматривается тенденция постепенного роста. Что ж, мы тоже будем действовать постепенно.

Уже знакомым нам способом выделим в отклонениях колебания с периодом 3 месяца.

Для этого:

  1. Создадим копию листа «Шаг 2», переименуем эту копию в «Шаг 3»;
  2. В ячейку В3 запишем формулу: ='Шаг 2'!E3 и автозаполнителем скопируем ее в ячейки В4:В26;
  3. В ячейке Н3 укажем затравочное значение для A3; подойдет ноль;
  4. В ячейке I3 укажем затравочное значение для B3; можно начать с 1000;
  5. В ячейке К3 укажем период: 3;
  6. В ячейке J3 укажем затравочное значение для C6: 0;
  7. Выделим ячейку F27 и выполним «Поиск решения».

Результатом будет A3=0, B3=608 и C3=–0,566; коэффициент детерминации
R2=0,354638 > 0,16284. Таким образом, и эту корреляцию следует признать существенной.

Теперь займемся периодом 4 месяца.

  1. Создадим копию листа «Шаг 3», переименуем эту копию в «Шаг 4»;
  2. В ячейку В3 запишем формулу: ='Шаг 3'!E3 и автозаполнителем скопируем ее в ячейки В4:В26;
  3. В ячейке Н3 укажем затравочное значение для A4: 0;
  4. В ячейке I3 укажем затравочное значение для B4: 500;
  5. В ячейке К3 укажем период: 4;
  6. В ячейке J3 укажем затравочное значение для C4: 0;
  7. Выделим ячейку F27 и выполним «Поиск решения».

A4=0, B4=543 и C4=–0,168; коэффициент детерминации R2=0,438435 > 0,16284. Корреляция существенна.

Вопрос о природе этих периодов адресуем все тем же маркетологам. Фантазии: ритм 4 месяца — это Рождество, Пасха, начало учебного года. Ритм 3 месяца — сдача квартальных отчетов в налоговые инспекции (как тут не наесться мороженым?). Но вернемся к нашим цифрам: на рис. 5 показаны графики базовой линии прогноза, суммы всех выделенных периодических трендов и отклонений суммы трендов от базовой линии.

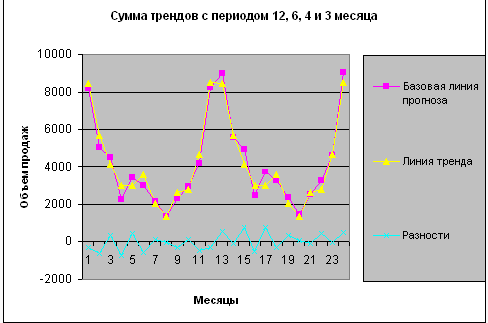
Сумма трендов с периодом 12, 6, 4 и 3 месяца

Рисунок 5 – Сумма трендов с периодом 12, 6, 4 и 3 месяца

Больше статистически значимых периодических трендов в наших наблюдениях выделить не удастся. Но у нас еще остался возрастающий тренд. Какую аппроксимацию выбрать для него? Если величина тренда невелика по сравнению со значениями базового ряда, то лучше всего выбирать линейную аппроксимацию, т.к. какой бы ни была реальная функция тренда, в первом приближении можно ограничиться линейным членом разложения в ряд Тейлора. Итак, ищем аппроксимацию :

  1. Создадим копию листа «Шаг 4», переименуем эту копию в «Шаг 5»;
  2. В ячейку В3 запишем формулу: ='Шаг 4'!E3 и автозаполнителем скопируем ее в ячейки В4:В26;
  3. В ячейку Н3 запишем формулу =ОТРЕЗОК(B3:B26;A3:A26) ; с помощью этой формулы рассчитывается величина AL;
  4. В ячейку I3 запишем формулу =НАКЛОН(B3:B26;A3:A26) ; с помощью этой формулы рассчитывается величина BL.

Должно получиться AL=–310; BL=24,8.

  1. В ячейку D3 запишем формулу расчета линейного тренда с полученными параметрами: =H$3+I$3*A3 ; с помощью автозаполнителя скопируем ее в ячейки D4:D26.

Коэффициент детерминации для линейного тренда составляет 0,156414, что меньше 0,16284, таким образом, эта корреляция может быть расценена как несущественная. Но все не так плохо. Мы можем принять этот тренд, если смягчим требования: уменьшим доверительную вероятность с 0,95 всего до 0,94 (рис. 6).

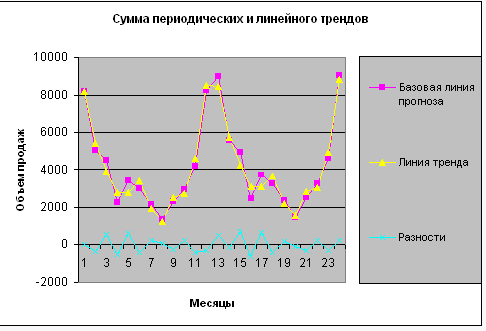
Сумма периодических и линейных трендов

Рисунок 6 – Сумма периодических и линейных трендов

Далее будем следовать методу Кошечкина–Бондаренко. В соответствии с этим методом рассчитаем «сезонную компоненту», т.е. усредненные по периодам отклонения от модели.

  1. Создадим копию листа «Шаг 5», переименуем эту копию в «Шаг 6».
  2. В ячейку В3 запишем формулу: ='Шаг 5'!E3 и автозаполнителем скопируем ее в ячейки В4:В26.
  3. В ячейку D3 запишем формулу: =(B3+B15)/2 ; с помощью автозаполнителя скопируем ее в ячейки D4:D14.
  4. В ячейку D15 запишем ту же формулу: =(B3+B15)/2 , и с помощью автозаполнителя скопируем ее в ячейки D16:D26.
  5. В ячейке D27 рассчитаем сумму сезонной компоненты: за 2 периода она равна 9,66´10–13, т.е. практически равна нулю. По Кошечкину–Бондаренко это — признак сезонности.
  6. Создадим копию листа «Шаг 1», переименуем эту копию в «Шаг 7».
  7. В ячейку D3 запишем формулу: ='Шаг 1'!D3+'Шаг 2'!D3+'Шаг 3'!D3+'Шаг 4'!D3+'Шаг 5'!D3+'Шаг 6'!D3; с помощью автозаполнителя скопируем ее в ячейки D4:D26.
  8. В ячейку Q3 запишем формулу расчета относительных квадратов отклонений модели, которые А.В.Бондаренко почему–то называет среднеквадратичными отклонениями: =(E3/D3)*(E3/D3); с помощью автозаполнителя скопируем формулу в ячейки Q4:Q26.
  9. В ячейку Q27 запишем формулу вычисления среднего относительного квадрата отклонения модели: =СУММ(Q3:Q26)/H27 ; оно равно 0,000597 (сравните с данными в Таблице 8 у А.В. Бондаренко — лучшее значение для линейного тренда составляет 0,0019; таким образом, точность нашей модели по А.В. Бондаренко составляет 99,94%).
  10. Относительное среднеквадратичное отклонение будет равно корню квадратному из среднего относительного квадрата отклонения; вычислим его в ячейке Р27: =КОРЕНЬ(Q27)

Диаграмма листа «Модель» покажет график нашей модели — см. рис.7. Коэффициент детерминации модели равен 0,99279.

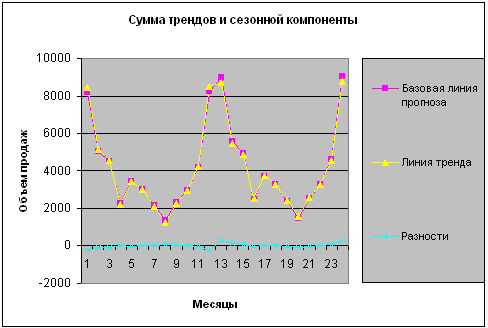
Сумма трендов и сезонной составляющей

Рисунок 7 – Сумма трендов и сезонной составляющей

К сожалению, наших данных недостаточно, чтобы судить о распределении ошибок модели. Поэтому будем строить доверительные интервалы, лишь уповая на нормальность распределения ошибок. Доверительный интервал для доверительной вероятности a рассчитывается по формулам; число наблюдений в базовом ряду, Отн.СКО – относительное среднеквадратичное отклонение.

  1. В ячейки R3, S3 запишем формулы расчета границ доверительных интервалов: =D3*(1–P$27*I$27/КОРЕНЬ(H$27)) и =D3*(1+P$27*I$27/КОРЕНЬ(H$27)) соответственно; с помощью автозаполнителя скопируем эти формулы в ячейки R4:R26 и S4:S26.

И, наконец, настала пора перейти к собственно прогнозированию на основе построенной модели. Для этого

  1. На листах «Шаг 1» — «Шаг 7» в ячейках А27:А38 запишем номера периодов с 25 по 36;
  2. На листах «Шаг 1» — «Шаг 5», «Шаг 7» формулу из ячейки D26 автозаполнителем скопируем в ячейки D27:D38;
  3. На листе «Шаг 6» в ячейку D27 запишем формулу =(B3+B15)/2 и с помощью автозаполнителя скопируем ее в ячейки D28:D38;
  4. На листе «Шаг 7» формулы из ячеек R26 и S26 автозаполнителем скопируем в ячейки R27:R38 и S27:S38.

Прогнозируемый объем продаж, верхняя и нижняя границы доверительных интервалов находятся в ячейках D27:D38, R27:R38 и S27:S38 листа «Шаг 7» соответственно. Они же представлены в таблице 2.

Таблица 2 – Прогнозируемые объемы реализации продукции

№ п.п. Месяц Прогнозируемый объем продаж (руб.) Верхняя граница доверительного интервала (руб.); a=0,95 Нижняя граница доверительного интервала (руб.); a=0,95
25 июль 9030,028 9123,176 8936,88
26 август 5779,153 5838,767 5719,539
27 сентябрь 5179,468 5232,896 5126,04
28 октябрь 2816,958 2846,016 2787,9
29 ноябрь 4017,633 4059,077 3976,19
30 декабрь 3564,053 3600,818 3527,289
31 январь 2701,403 2729,269 2673,537
32 февраль 1838,748 1857,716 1819,781
33 март 2852,408 2881,832 2822,985
34 апрель 3547,913 3584,511 3511,315
35 май 4874,003 4924,28 4823,726
36 июнь 9085,856 9179,58 8992,132

В этом месте самое время делать высоконаучные выводы о том, как надо прогнозировать. Но вместо этого автор решил рассказать поучительную историю.

Не далее, как ранней осенью 2006 года автор делал по заказу одного из своих клиентов прогноз продаж женских сумочек на осень/зиму 2006/2007 гг. В распоряжении автора были наблюдения за 5 предшествующих лет. Модель получилась красивой и очень статистически достоверной. Но, как вы наверное уже догадываетесь, прогноз провалился. Да не просто провалился, и даже не с треском провалился, а провалился со свистом и грохотом! А вся штука оказалась в том, что из–за аномально теплой зимы украинские дамы не одели шубки, а проходили зиму в осенних пальто и кардиганах, и им не понадобилось менять сумочки на сугубо зимние! Мораль сей истории такова: пока существенный фактор влияния на спрос ведет себя стабильно, вы можете даже не подозревать о его существовании. И прогнозировать, прогнозировать, прогнозировать… Но у этой «медали» есть и обратная сторона: изучайте факторы влияния на спрос, учитывайте их в математических моделях, и ваши прогнозы будут чаще сбываться. А пример того, как в MS Excel построить модель с практически любой функциональной зависимостью, как раз и дала вам эта статья.

Дата публикации: 03.04.2007