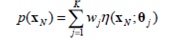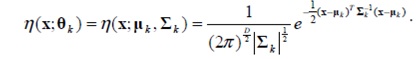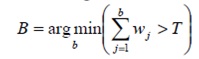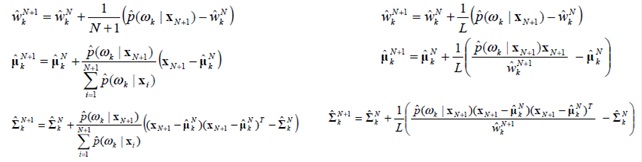Резюме
В режиме реального времени сегментация движущихся областей в последовательности изображений является важным шагом во многих системах зрения, включая автоматизированные системы визуального наблюдения, человеко-машинные интерфейсы, и телекоммуникации с очень низкой пропускной способностью. Типичный метод – вычитание фона. Многие модели фона были введены для решения различных задач. Одним из удачных решений этой проблемы является использование многоцветной модели фона для каждого пикселя, предложенной Гримсоном и соавторами [1-3]. Однако этот метод страдает от медленного обучения в начале, особенно в загруженных средах. Кроме того, он не может отличить движущиеся тени и движущиеся объекты. Эта статья описывает метод, который улучшает эту адаптивную смешанную модель фона. Повторно исследуя уравнения обновления, мы используем различные уравнения в различных фазах. Это позволяет нашей системе учиться быстрее и точнее, а также адаптироваться к изменениям окружающей среды. Схема обнаружения тени также представлена в данной статье. Она основана на вычислимом цветовом пространстве, что позволяет использвать нашу модель фона. Было сделано сравнение между двумя алгоритмами. Результаты показывают скорость обучения и точность модели с использованием нашего алгоритма обновления на основе трекере Гримсона и соавторов. В соединении с обнаружением теней, наш метод приводит к гораздо лучшей сегментации, чем метод Гримсона и соавторов.
1. Введение
Вычитание фона включает в себя расчет эталонного изображения, вычитание каждого нового кадра из этого образа и пороговых значений. Результат – это двоичная сегментация изображения, которая выдвигает на передний план регионы нестационарных объектов. Простейшая форма эталонного изображения является усредненным по времени фоном изображения. Этот метод страдает от многих проблем и требует наличия периода обучения с отсутствием переднеплановых объектов. Движущиеся фоновые объекты после периода обучения и неподвижные объекты переднего плана в период обучения будут рассматриваться в качестве постоянных объектов на переднем плане. Кроме того, данный подход не может справиться с постепенными изменениями освещения в сцене. Эти проблемы приводят к требованию, чтобы любое решение должно постоянно переоценивать модель фона. Многие адаптивные фономоделирующие методы были предложены для решения этих медленно меняющихся стационарных сигналов. Фридман и Рассел смоделировали каждый пиксель камеры сцены с помощью адаптивной параметрической смешанной модели из трех гауссовских распределений [4]. Они также проводят краткие рассуждения по онлайн уравнениям обновления на основе достаточной статистики. Коллер и соавторы использовали фильтр Кальмана для отслеживания изменений в освещении фона для каждого пикселя [5]. Они применяют выборочную схему обновления, включающую в себя только наиболее вероятные значения фона в оценке фона. Методы могут хорошо справляться с изменением освещения, однако, не могут решить проблему появления и исчезновения объектов в сцене. Одно из решений заключается в использовании нескольких цветовых моделей фона для каждого пикселя. Гримсон и соавторы разработали адаптивную непараметрическую гауссовскую смешанную модель для решения этих проблем [1-3]. Их модель может также уменьшить влияние небольших повторяющихся движений, например, движение растительности деревьев и кустарников, а также небольшое смещение камеры. Эль-Гаммаль и соавторы использовали ядра оценки для каждого пикселя [6]. Образцы ядер были взяты из движущегося окна. Они также ввели метод снижения результатов небольшого движения за счет использования пространственной когерентности. Это было сделано путем сравнения односвязных компонентов модели фона с ее круговой окрестностью. Хотя авторы представили ряд процедур ускорения, подход по-прежнему имеет высокую вычислительную сложность. Были предложени и другие методы с использованием высокоуровненой обработки для поддержки моделирования фона; например, трекер Wallflower [7], который обходит некоторые из этих проблем с использованием высокоуровневой обработки, а не решением недостатков модели фона. Наш метод основан на фреймворке Гримсона и соавторов [1-3], различия заключаются в уравнениях обновления, методе инициализации и внедрении алгоритма обнаружения тени.
В качестве общей схемы оптимизации, используемой в соответствии с гауссовской смешанной моделью, применяется алгоритм максимизации ожидания (EM). Алгоритм EM является итерационным методом, который гарантирует схождение к локальному максимуму в пространстве поиска. В связи с пространственно-временными требованиями для моделирования каждого пикселя на фоновом изображении требуется онлайн алгоритм EM. Было предложено большое число онлайн алгоритмов EМ. Их можно разделить на две группы. Первая группа работает в области параметрической оценки функции плотности вероятности. Другими словами, происходит использование новых данных при обновлении предыдущей оценки без внесения изменений в структуру предыдущей модели. Процедура была введена Ноуланом [8] и объяснена в терминах результатов Нила и Хинтона [9]. Трейвен вывел версию процедуры с N-последними окнами [10]. МакКенна и соавторы [11-13] расширили результат Трейвена [10] до L-последних окон как результат работы L-групп алгоритмов EM и использовали их для отслеживания многоцветного объекта на переднем плане. Этот параметрический подход к оценке не может работать эффективно без хорошей первоначальной оценки (как правило, она находится работой группы алгоритмов EM). Вторая группа использует непараметрические подходы. Прибэ и соавторы предложили адаптивную смешанную модель со стохастическим порогом для создания новых ядер Гаусса в существующей смешанной модели [14,15]. Гримсон и Стауффер [2,3], однако, применили ту же схему с использованием детерминированного порога.
В дополнение к Гримсону и соавторам, многие другие авторы применили смешанную модель для моделирования каждого пикселя в сценах камеры. Роу и Блейк применяют группу алгоритмов EM для оффлайн обучения в виртуальной плоскости изображения [16]. Тем не менее, модель не обновляется с течением времени и, следовательно, ведет к сбоям во внешних средах, где освещение сцены меняется со временем. Фридман и Рассел смоделировали дорогу, расположение теней и транспорта для каждого пикселя с использованием адаптивной смеси трех распределений Гаусса [4]. Классификация основана на эвристическом методе относительных расстояний в пространстве. Они сообщили о хорошей сегментации при использовании ожидаемых достаточных статистических уравнений. Однако, все еще требуется выполнение предварительной обработки для обучения исходной модели с использованием группы алгоритмов EM.
Мы описываем модель фона, предложенную Гримсоном и Стауффером [2,3] и ее недостатки в разделе 2.1. Предлагаемое нами решение проблемы представлено в разделе 2.2. Раздел 2.3 объясняет наш алгоритм обнаружения тени. Результаты каждого метода приводятся и сравниваются в разделе 3 и делаются выводы в разделе 4.
2. Моделирование фона
В этом разделе мы рассматриваем работу Гримсона и Стауффера [2,3], и ее недостатки. Авторы вводят метод для моделирования каждого пикселя фона смесью K-распределений Гаусса (К – небольшое число от 3 до 5). Различные Гауссианы, как предполагается, представляют собой различные цвета. Весовые параметры смеси представляют временные пропорции, в течение которых цвета остаются в сцене. В отличие от работы Фридмана и соавторов, компоненты фона определяются в предположении, что фон B содержит наивысшие возможные цвета. Вероятными цветами фона являются те, которые дольше наблюдаются и более статичны. Статические одноцветные объекты имеют тенденцию образовывать тесные скопления в цветовом пространстве, в то время как при движении определенных форм происходит расширение скоплений за счет различных отражающих поверхностей во время движения. В их документах это измерение было названо значением соответствия. Чтобы обеспечивать адаптацию модели к изменениям освещения и работу в режиме реального времени, была применена схема обновления. Она основана на выборочной модификации. Каждое новое значение пикселя проверяется в порядке соотвествия с существующими компонентами модели. Первая модель сравнения компонент обновляется. Если она не находит соответствия, новая компонента Гауссиана будет добавлена к среднему на тот момент, к большой ковариационной матрице и к малому значению весовых параметров.
2.1 Адаптивная гауссовская смешанная модель
Каждый пиксель в сцене моделируется смесью K распределений Гаусса. Вероятность того, что определенный пиксель имеет значение xn во время N можно представить в виде
где wk- вес параметра k-й компоненты Гауссиана, η(x,Θk) – нормальное распределение k-й компоненты, представленное
где μk – среднее и Σk=σk2I – ковариация k-й компоненты.
К-распределения упорядочены по значению соответствия wk/σk и B-первые распределения используются в качестве модели фона сцены, где B оценивается как
Порог Т – минимальная доля модели фона. Другими словами, это минимальная предварительная вероятность того, что фон есть в сцене. Вычитание фона осуществляется меткой передпланового пикселя любого пикселя, который имеет более чем 2.5 стандартных отклонения от любого из B-распределения. Первый компонент Гауссиана, который соответствует тестовому значению будет обновляться следующими уравнениями обновления,
где ωk является k-й компонентой Гауссиана, 1/α определяет константу времени, которая устанавливает изменения. Если ни одно из К-распределений не совпадает со значением пикселя, наименее вероятный компонент заменяется распределением с текущим значением, как его среднее, изначально высокая дисперсия, низкий параметр веса. В соотвествии с работами [1-3], только два параметра – α и T – необходимо установить в системе.
Детали надежности были объяснены в работах [1-3], однако, проведя небольшое обусждение, можно увидеть недостатки. Во-первых, если первое значение данного пикселя – переднеплановый объект, то существует только один Гауссиан, где его вес равен единице. При наличии только одноцветной фоновой последовательности, будет обработано log1-α(T) кадров, пока подлинный фон станет рассматриваться в качестве фона и log1-α(5) кадров, пока не станет доминирующей фоновой компонентой. Например, если предположить, что не менее 60% времени фон присутствует и α составляет 0.002 (500 последних кадров), то потребуется 255 кадров и 346 кадров для компонента, чтобы включить его как часть фона и как часть доминирующей фоновой компоненты, соответственно. Ситуация может быть хуже в оживленных местах, где чистый фон редко встречается. Эта статья предлагает решение проблемы в следующем разделе. Во-вторых, ρ может быть слишком небольшим из-за вероятностного фактора. Это приводит к слишком медленной адаптации средних значений и ковариационных матриц, поэтому трекер может выйти из строя в течение нескольких секунд после инициализации. Одним из решений этой проблемы является просто вырезать элемент вероятности из ρ.
2.2 Онлайн алгоритмы EM
Мы начинаем нашу оценку гауссовской смешанной модели ожидаемыми достаточными статистическими уравнениями обновления, а затем переключимся на версию L-последних окон, когда обрабатываются первые L-образцов. Ожидаемые достаточные статистические уравнения обновления обеспечивают хорошую оценку в начале перед сбором всевозможных L-образцов. Эта первоначальная оценка повышает точность оценки, а также производительность трекера, обеспечивая быструю сходимость к устойчивой модели фона. Уравнения обновления L-последних окон дают приоритет над последними данными, поэтому трекер может адаптироваться к изменениям в окружающей среде.
Онлайн алгоритмы EM ожидаемой достаточной статистики приведены в левой колонке, а версия L-последних окон – в правой.
2.3 Определение тени и цветовая модель
Как свидетельствуют авторы в своих работах [1-3], трекер Гримсона и соавторов не может отделить движущиеся тени от объектов, которые их отбрасывают. Причиной этого является то, что не существует эвристики для маркировки компонент Гауссиана как движущхся теней. Одно из решений заключается в использовании хроматического пространства представления цвета, которое уменьшает восприимчивость. Так как многие цветовые пространства могут разделять хроматические компоненты и компоненты освещения, сохранение хроматической модели независимо от яркости может привести к неустойчивой модели, особенно для очень ярких или темных объектов. Это преобразование также требует вычислительных ресурсов, особенно в больших изображениях. Идея сохранения интенсивности компонентов и сохранение вычислительных затрат приводит нас обратно в пространство RGB. Как требование для идентифицикации движущихся теней, мы должны рассмотреть цветовую модель, которая может разделять хроматические компоненты и компоненты яркости. Она должна быть совместима и использовать нашу смешанную модель. Это делается путем сравнения пикселя, не принадлежащего фону, с текущим компонентом фона. Если разница и в хроматической компоненте, и в компоненте яркости имеет некоторое пороговое значение, пиксель считается тенью. Мы используем эффективную модель вычисления цвета, похожую на предложенную Хорпрасертом и соавторами [17] для выполнения этих задач. Она состоит из радиус-вектора в RGB средних пикселя фона (E), ожидаемой цветности линии (||E||), хроматического искажения (d), и порога яркости, τ. Для данного наблюдаемого значения пикселя (I), искажение яркости (а) и искажение цвета (с) из модели фона могут быть рассчитаны как
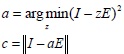
С предположением сферического гауссовского распределения в каждой смеси компонентов, стандартное отклонение k-й компоненты σk может быть принято равным d. Расчет a и с тривиален с использованием векторного или скалярного произведения. Наблюдаемый образец, не принадлежащий фону, считается движущейся тенью, в нашем случае, если находится в пределах 2.5 стандартных отклонений и τ <с <1.
3. Испытания
Этот раздел демонстрирует эффективность модели Гримсона [2,3] и предлагаемого алгоритма на последовательности изображений. Последовательности, используемые здесь, являются изображениями размером 192х144. Мы использовали адаптивную смесь из пяти компонент Гауссианов. L был установлен равным 500 кадров (α = 0.002 у Гримсона и соавторов) и порог T была установлен на уровне 0.6. В модуле обнаружения тени был использован порог яркости τ равный 0.7. Более высокоуровневые процессы, такие как очистка шумов или алгоритмы анализа связанных компонент, не были введены в алгоритм вычитания фона для отображения производительности модели фона. На рисунке 1 показана последовательность изображений загруженной сцены на открытой местности, содержащей людей, идущих по тротуару. Последовательность включает в себя солнечный свет, большие затененные области, дерево, отражения от окон и длительные перемещения теней. Мы представили изображения на начальном этапе, в загруженном виде и в долгосрочной перспективе. Из-за загрязненного изображения в начале, артефакты исходного изображения остаются в трекере Гримсона и соавторов на протяжении более ста кадров. Лучшая сегментация видна при использовании нашего метода. Производительность резко повышается с использованием модуля обнаружения тени.
4. Выводы
Мы представили новый алгоритм обновления для обучения адаптивных смешанных моделей фона сцены для отслеживания движущихся объектов в режиме реального времени. Алгоритм запускается в рамках надежного трекера реального времени, предложенного Гримсоном и соавторами. Было сделано сравнение между двумя алгоритмами. Результаты показывают скорость обучения и точность модели при использовании нашего алгоритма обновления над трекером Гримосна и соавторов. Мы предложили метод обнаружения движущихся теней с использованием существующей смешанной модели. Это значительно сокращает дополнительные вычислительные затраты. Обнаружение тени выполняется только над пикселями, помеченными как передний план и, следовательно, с незначительными вычислительными затратами движущиеся тени могут быть обнаружены успешно. Обнаружение тени также уменьшает влияние небольших повторяющихся движений на фоне сцены.

Рисунок 1 – В верхней строке отображается исходная последовательность в 15, 105, 235, 290 и 1200 кадров соответственно. Во второй строке показаны результаты Гримсона и соавторов. Последние две строки – результаты предлагаемого нами метода с и без движущихся теней. Тени представлены серым цветом
Литература
1. Grimson Wel, Stauffer C. Romano R. Lee L. Using adaptive tracking to classify and monitor activities in a site. in Proceedings. 1998 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No.98CB36231). IEEE Comput.Soc. 1998. 1998.
2. Stauffer C, Grimson W. E. L. Adaptive background mixture models for real-time tracking. in Proceedings. 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149). IEEE Comput. Soc. Part Vol. 2, 1999.
3. Stauffer C, Grimson W. E. L., Learning patterns of activity using real-time tracking. IEEE Transactions on Pattern Analysis &Machine Intelligence, 2000. 22(8): p. 747-57.
4. Friedman N., Russell S. Image Segmentation in Video Sequences: A Probabilistic Approach. in The Thirteenth Conference on Uncertainty in Artificial Intelligence. 1997. Brown University, Providence, Rhode Island, USA: Morgan Kaufmann Publishers, Inc., San Francisco, 1997.
5. Koller D, Weber J. Huang T. Malik J. Ogasawara G. Rao B. Russell S. Towards robust automatic traffic scene analysis in realtime.in Proceedings of the 33rd IEEE Conference on Decision and Control (Cat. No.94CH3460-3). IEEE. Part vol.4, 1994. 1994.
6. Elgammal A., Harwood D., Davis L. non-parametric model for background subtraction. in IEEE ICCV'99 FRAME-RATEWORKSHOP. 1999.
7. Toyama K, Krumm J. Brumitt B. Meyers B. Wallflower: principles and practice of background maintenance. in Proceedings ofthe Seventh IEEE International Conference on Computer IEEE Comput. Soc. Part vol.1, 1999. 1999.
8. Nowlan, S. J., Soft Competitive Adaptation: Neural Network Learning Algorithms based on Fitting Statistical Mixtures, in Schoolof Computer Science. 1991, Carnegie Mellon University: Pittsburgh, PA.
9. Neal, R. M., Hinton, G. E., A view of the EM algorithm that justifies incremental, sparse, and other variants, in Learning inGraphical Models, M. I. Jordan, Editor. 1998, Dordrecht: Kluwer Academic Publishers. p. 355-368.
10. Traven, H. G. C., A neural network approach to statistical pattern classification by 'semiparametric' estimation of probabilitydensity functions. IEEE Transactions on Neural Networks, 1991. 2(3): p. 366-77.
11. McKenna Sj, Raja Y. Shaogang Gong, Object tracking using adaptive colour mixture models. Computer Vision – ACCV '98.Third Asian Conference on Computer Vision. Proceedings. Springer-Verlag. Part vol.1, 1997, 1998: p. 615-22 vol.
12. Raja Y, McKenna S. J. Gong S., Color model selection and adaptation in dynamic scenes. Computer Vision – ECCV'98. 5thEuropean Conference on Computer Vision. Proceedings. Springer-Verlag. Part vol.1, 1998, 1998: p. 460-74 vol.
13. Raja Y, McKenna S. J. Shaogang Gong, Segmentation and tracking using colour mixture models. Computer Vision – ACCV '98.Third Asian Conference on Computer Vision. Proceedings. Springer-Verlag. Part vol.1, 1997, 1998: p. 607-14 vol.
14. Priebe Ce, Marchette D. J., Adaptive mixtures: recursive nonparametric pattern recognition. Pattern Recognition, 1991. 24(12):p. 1197-209.
15. Priebe Ce, Marchette D. J., Adaptive mixture density estimation. Pattern Recognition, 1993. 26(5): p. 771-85.
16. Rowe S., Blake A. Statistical background modelling for tracking with a virtual camera. in BMVC `95 Proceedings of the 6th British Machine Vision Conference. BMVA Press. Part vol.2, 1995. 1995.
17. Horprasert T., Harwood D., Davis L.S. a statistical approach for real-time robust background subtraction and shadow detection.in IEEE ICCV'99 FRAME-RATE WORKSHOP. 1999.