Вернуться в библиотеку

ВАРИАНТЫ ЭФФЕКТИВНОЙ РЕАЛИЗАЦИИ ПОСТБИНАРНЫХ КЛЕТОЧНЫХ АВТОМАТОВ

Автор: Аноприенко А.Я., Плотников Д.Ю., Малёваный Е.Ф., Коноплёва А.П.
Источник: Электронный архив ДонНТУ, http://ea.donntu.ru...

В статье исследуется вопрос распараллеливания алгоритмов клеточных автоматов на примере игры «жизнь». Для исследования эффективности распараллеливания было разработано две программы. В первой версии в основе лежит стандартный алгоритм клеточного автомата, во второй предусмотрено распараллеливание алгоритма на несколько процессоров с использованием библиотеки MPI.

На настоящее время перед специалистами в области информационных технологий стоит задача гармоничной разработки программного обеспечения и аппаратных средств. Но на практике существует немного программ, которые используют возможности новейшей аппаратуры на максимум. Постбинарные клеточные автоматы позволяют проводить реалистичное моделирование динамических процессов. Основным недостатком моделирования с помощью данной технологии является обработка большого количества элементов.

Решение задачи

Авторы поставили перед собой задачу исследовать возможность распараллеливания алгоритмов клеточных автоматов. В качестве алгоритма был выбран стандартный алгоритм иры «жизнь». Программное обеспечение написано на языке С++ в среде Borland C++ Builder. Интерфейс программы изображен на рисунке 1. В первой версии программы реализован последовательный алгоритм клеточного автомата. Моделирование игры жизнь осуществляется на поле размером 32*32 клетки. В ходе моделирования можно выбирать тип соседства клеток – соседство фон Неймана или соседство Мура, которые изображены на рисунке 2.

Рисунок 1 – Интерфейс программы

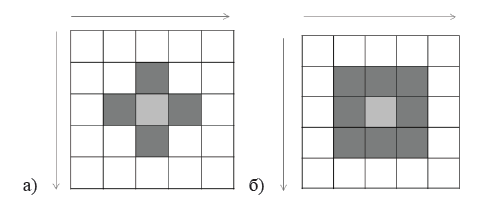
Рисунок 2 – Типы соседства в клеточном автомате, используемые в программе: а) модель фон Неймана; б) модель Мура

В зависимости от типа соседства на каждую клетку влияет различное количество соседей. Соседство фон Неймана предусматривает, что на клетку влияет только 4 соседа – слева и справа по горизонтали, сверху и снизу по вертикали. В соседстве Мура добавляется еще 4 соседа по диагонали. Две модели соседства в программе используются для того, чтобы можно было оценить эффективность разных алгоритмов, а также возможность их применения для моделирования различных процессов.

Для задания начального состояния клеточного автомата можно использовать два способа: рисовать клетки автомата вручную, а также задавать начальные состояния с помощью тетралогики. Тетралогика – это логика четвертого порядка, которая помимо значений 0 и 1 включает неопределенность А и множественность М. Неопределенность А – значение либо 0, либо 1 с долей вероятности 50%. Множественность М – это значение 0 и 1 одновременно. Таким образом, число 1А может быть как 10, так и 11. Число 1М – это 10 и 11 одновременно. Если в данной программе задать координаты МММММ для оси Х и У, то все поле заполнится клетками.

Клеточные автоматы являются очень удобными для распараллеливания. В идеале для обработки каждой клетки можно выделить свой процессор. Параллельный алгоритм «жизни» был реализован с использованием библиотеки MPI. Моделирование производилось на кластере. Для сравнения эффективности работы разных версий программы было проведено 3 этапа моделирования:

1. Моделирование последовательной версии программы на одном узле кластера.
2. Моделирование параллельной версии программы на одном узле кластера.
3. Моделирование второй версии программы с распараллеливанием на 8 узлах кластера.

По результатам моделирования второй версии программы был построен график зависимости времени обработки от количества используемых узлов, который изображен на рисунке 3. По оси Х - количество узлов. По оси У – время выполнения задачи.

Рисунок 3 – График зависимости времени моделирования от количества используемых узлов кластера

Из результатов моделирования видно, что скорость работы программы увеличивается практически в 8 раз. При увеличении количества используемых узлов график будет изменяться по экспоненциальному закону. Была разработана программа на CUDA для проверки эффективности реализации. Для этих целей была выбрана CUDA (Compute Unified Device Architecture) – программно-аппаратная архитектура, позволяющая производить массивно-параллельные вычисления с использованием графических процессоров NVIDIA, поддерживающих технологию GPGPU (произвольных вычислений на видеокартах). На сегодняшний день продажи CUDA процессоров достигли 128 миллионов. Тысячи разработчиков программного обеспечения, ученых и исследователей широко используют CUDA в различных областях, включая обработку видео, астрофизику, вычислительную биологию и химию, моделирование динамики жидкостей, электромагнитных взаимодействий, восстановление изображений, полученных путем компьютерной томографии, сейсмический анализ, трассировку луча и многое другое.

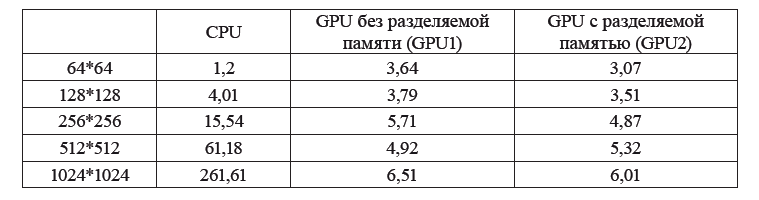
Таблица 1. Быстродействие ПКА для CPU, GPU без разделяемой памяти, GPU с разделяемой памятью при различных размерностях

Выводы

Моделирование клеточного автомата на кластере показывает, что работа программы ускоряется практически линейно с увеличением количества используемых узлов. Таким образом, распараллеливание клеточных автоматов является эффективным. В дальнейшем планируется разработка программы с использованием технологии OpenCL и распараллеливание на процессорах современных видеокарт. Также планируется параллельная реализация других алгоритмов для моделирования динамических процессов на базе клеточных автоматов.

Литература

[1] Тофоли Т., Марголус Н. Машины клеточных автоматов. – М.: «Мир», 1991. 280с.

[2] Беркович С.Я. Клеточные автоматы как модель реальности: поиски новых представлений информационных и физических процессов. – М.: Издательство МГУ, 1993. - 112 с.

[3] Schiff J. L. Cellular automata: a discrete view of the world. A John Wiley&Sons inc, Publication. University of Auckland. – 2008. – 279 p.

[4] Аладьев В.З. Классические однородные структуры. Клеточные автоматы. Fultus Publishing – 2009. – 535 с.

[5] Ландэ Д.В., Фурашев В.Н. Моделирование электоральных процессов на основе концепции клеточных автоматов // Открытые информационные и компьютерные интегрированные технологии. – Харьков: НАКУ, 2007. – Вып. 36. – С. 123-128, http:// poiskbook.kiev.ua/art/x36/klet-vyb.pdf.

[6] Аноприенко А.Я., Плотников Д.Ю., Малёваный Е.Ф., Моделирование реальных вероятностных процессов на базе клеточных автоматов с ограничениями // Збірка матеріалів I Всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених ІУС ТА КМ-2010 Аноприенко А.Я., Плотников

[7] Д.Ю., Малёваный Е.Ф. Использование клеточных автоматов для моделирования движения транспорта. Збірка праць VI міжнародної науково-технічної конференції студентів, аспірантів та молодих науковців «Інформатика та комп’ютерні технології» 2010 р.

[8] Аноприенко А.Я., Плотников Д.Ю., Моделирование поведения толпы людей на базе клеточных автоматов // Збірка матеріалів II Всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених ІУС ТА КМ-2011.

[9] GrowCut: Image cutout & matting tool, http://growcut.com.

[10] Аноприенко А.Я., Коноплева А.П. Управляемые и неуправляемые постбинарные клеточные автоматы // Материалы V Всеукраинской научно-практической конференции «Современные тенденции розвития информационных технологий в науке, образовании и экономике», Луганск, 7-8 апреля 2011 г., том 1.