Forschungsgebiet: parallele Simulationstechnik

L. P. Feldmann, V. A. Svjatnyj

svjatnyj@cs.donntu.ru

M. Resch, M. Zeitz

resch@hlrs.de; zeitz@isys.uni-stuttgart.de

---

Источник: Национальная библиотека Украины имени В.И. Вернадского. Научные работы Донецкого национального технического университета. Серия: Проблемы параллельного моделирования и автоматизации проектирования

---

Анотація

Фельдман Л.П., Святний В.А., Реш М., Цайтц М. Наукова область: паралельне моделювання. Паралельне моделювання як актуальний науковий напрямок досліджується впродовж ряду останніх років в рамках співпраці науковців Штуттгартського та Донецького національного технічного університетів. Головною проблемою є розробка високопродуктивного і дружнього до користувачів моделюючого середовища з ефективним використанням паралельних апаратно-програмних ресурсів. За допомогою середовища і чисельних методів досліджуються моделі складних динамічних систем з зосередженими і розподіленими параметрами. Як приклади подано моделі систем шахтної вентиляції та технологічних процесів у відповідних проблемно орієнтованих паралельних моделюючих середовищах.

Ключові слова: паралельне моделювання, моделююче середовище, чисельні методи, паралельний симулятор, технологічні процеси.

Аннотация

Фельдман Л.П., Святный В.А., Рэш М., Цайтц М. Научная область: параллельное моделирование. Параллельное моделирование как актуальное научное направление исследуется на протяжении ряда последних лет в рамках сотрудничества учёных Штутгартского и Донецкого национального технического университетов. Главной проблемой является разработка высокопродуктивной и дружественной к пользователю моделирующей среды с эффективным использованием параллельных аппаратно-программных ресурсов. С помощью среды и численных методов исследуются модели сложных динамических систем с сосредоточенными и распределёнными параметрами. В качестве примеров приведены модели систем шахтной вентиляции и технологических процессов в соответствующих проблемно ориентированных параллельных моделирующих средах.

Ключевые слова: параллельное моделирование, моделирующая среда, численные методы, параллельный симулятор, технологические процессы.

Kurzfassung

Feldmann L.P., Svjatnyj V.A., Resch M., Zeitz M. Forschungsgebiet: parallele simulationstechnik. Die parallele Simulationstechnik wird im Rahmen einer langjährigen Kooperation von Informatikern und Simulationstechnikern der Universität Stuttgart und der Nationalen Technischen Universität Donezk als ein aktuelles Forschungsgebiet untersucht. Im Mittelpunkt steht dabei die Entwicklung einer leistungsfähigen und benutzerfreundlichen Simulationsumgebung mit einer effizienten Nutzung von parallelen Hard- und Softwareressourcen. Mit dem entwickelten Simulationswerkzeug werden komplexe Modelle von dynamischen Systemen mit konzentrierten und mit verteilten Parametern numerisch gelöst. Als Beispielprozesse werden Modelle von Grubenbewetterungssystemen und der Verfahrenstechnik in entsprechenden problemorientierten parallelen Simulationsumgebungen betrachtet.

Schlagwörter: parallele Modellierung und Simulation, Simulationsumgebung, numerische Verfahren, paralleler Simulator, verfahrenstechnische Prozesse.

Abstract

Feldmann L.P., Svyatnyy V.A., Resch M., Zeitz M. Research area: parallel simulation. Parallel simulation engineering as an actual research direction is investigated in course of a long term cooperation between Universität Stuttgart and Donetsk National Technical University. The major research goal concerns the development of an high performance and user friendly simulation environment with an efficient use of parallel hardware and middleware resources. The simulation environment and advanced numerical methods allow to investigate complex models of dynamical systems with specially lumped and distributed parameters. As benchmark example, the mathematical model of mine ventilation systems together with related automation problems are investigated.

Keywords: parallel modelling and simulation, simulation environment, numerical methods, parallel simulator, technological processes.

Einführung

Die Anwendungsgebiete der Simulationstechnik reichen sich von den "traditionellen" technischen dynamischen Systemen (DS) mit konzentrierten und mit verteilten Parametern (DSKP, DSVP) über biotechnologische und ökologische Prozesse bis hin zu den zu projektierenden und zu optimierenden Unternehmens-, Wirtschafts- und Öffentlichkeitsstrukturen. Die modellgestützte Entwicklung von komplexen technischen und nichttechnischen DS in allen Bereichen ist ein entscheidender Faktor zur Qualitätssicherung und Konkurrenzfähigkeit bei laufenden und zukünftigen technischen und technologischen Projekten. Als Folge von steigenden Anforderungen an die Qualität, Sicherheit und Wirtschaftlichkeit der DS-Prozesse werden immer genauere und damit auch komplexere Simulationsmodelle benötigt. Bei dieser Entwicklung ergibt sich in einer natürlichen Weise eine Komplexitätsschwelle für die Implementierung und Anwendung der Simulationsmodelle, die nur durch die Verwendung von neuen Simulationswerkzeugen überwunden werden kann. Hierzu gehören u.a. die parallelen Höchstleistungsrechner der MIMD-Architektur mit eng (über gemeinsamen Adressraum von Shared Memory) und lose (mit dem autonom zugeordneten Adressraum) gekoppelten Prozessoren sowie mit einer hybriden Speicherorganisation. Die effiziente Nutzung von diesen Simulationswerkzeuge erfordert eine benutzerfreundliche system- und informationstechnische Organisation der parallelen Ressourcen sowie eine hoch entwickelte Simulationssoftware, die neue Ansätze zur Modellerstellung und Simulationsdurchführung zur Verfügung stellt. Die hierbei zu lösenden theoretischen und praktischen simulationstechnischen Probleme gehören zum Fachgebiet der parallelen Simulationstechnik. Dieses Forschungsgebiet wird im Rahmen der langjährigen Kooperation von Informatikern und Simulations-technikern der Universität Stuttgart und der Nationalen Technischen Universität Donezk (Ukraine) untersucht.

Dynamische Systeme als Objekte der Modellierung und Simulation

Als dynamische werden die Objekte von Technik und Technologien bezeichnet, deren Betriebsart mit den Prozesse von Zustandsänderungen zeitabhängig charakterisiert wird. Diese Prozesse können von den Naturerscheinungen oder zielgerichteten Steuerungsaktionen für die Überführung der Objekte von gewissen Anfangszustand in bestimmten vordefinierten Zustand iniziirt werden. Jeder technischer Bereich, jede Technologie hat spezifischen dynamischen Objekte und Prozesse, die im Rahmen von verfahrenstechnischen Flißbilder sowie in der Integration mit den Automatisierungsmitteln folgende Eigenschaften von komplexen dynamischen Systemen (KDS) bekommen: große Anzahl und Mehrfachheit der Verbindungen von charakteristischen Parametern, die Nichtlinearität der statischen und dynamischen Charakteristiken der Komponenten, hierarchische Anordnung von Regelungsmitteln, die Abhängigkeit der Prozesse von zeitlichen und örtlichen Koordinaten, die physikalische Vielfältigkeit der zusammenwirkenden Prozesse, eine Wechselung der Strukture abhängig von Abläufen der dynamischen Prozesse, eine Vorhandenheit der Phasen und Bereiche von Parametern, die sicherheitskritische Zustände der Systeme verursachen können u. a. Wissenschaftstechnisches Niveau der jetzigen Gegenstandsgebiete (GG, Abb. 1) von der Bergbautechnik, des Hüttenwesens bis der Bioverfahrens- und Umweltschutztechnik wird in bedeutendem Ausmaß durch erreichte Wissensebene der Prozeßtheorie, des Verständnisses der Zusammenwirkungen und der Integration verschiedener dynamischen Prozesse sowie ihren praktischen Inbetriebnahmen von GG-Experten in KDS-Industrieprojekte bestimmt. KDS-Theorie vermittelt eine Annäherung der Gegenstandsgebiete (Abb.1) bei der kompletten Lösung von technischen und technologischen Problemen.

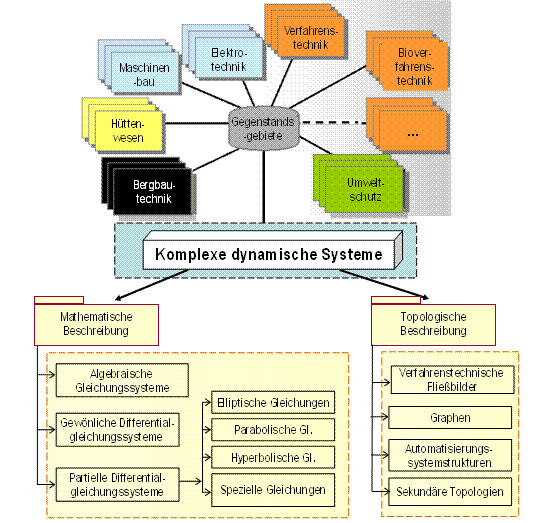
Aus simulationstechnischen Gründen werden zwischen dynamischen Systeme mit konzentrierten (DSKP) und örtlich verteilten (DSVP) Parametern unterscheidet. Traditionell gehören die Theorie und Simulationsverfahren von DSKP und DSVP zu den selbstständigen wissenschaftlichen Disziplinen. Forschungs- und Entwicklungspraktiken zeigen aber, dass die DSKP und DSVP oft als dieselben Objekte untersucht werden: üblicherweise wird ein Objekt erst als VP-Objekt analysiert, dann werden die weitere Untersuchungen durch eine Approximierung mit der gewissen Menge der KP-Objekte und der Behaltung von entsprechenden Approximationsbedingungen fortgesetzt.

Eine Analyse zeigt, daß trotzt breite physikalische DS-Vielfältigkeit der verschiedenen Gegenstansgebiete ihre Topologien mit der in Abb.1 illustrierten relativ begrenzten Menge von Darstellungsmitteln beschrieben werden: das sind die verfahrenstechnische Fließbilder (VTF), Strukturschemata der Automatisierungssysteme (SSA), durch den Graphen dargestellten dynamischen Netzobjekte (DNO) und die während der DSVP-Approximierung entstehenden sekundären Topologien (ST). Hauptziel der Topologiebeschreibung besteht in eindeutlichen Darstellung der DS-Struktur, der Bestandteile und ihrer Verbindungen sowie in der Integration mit der mathematischen Beschreibung in der Form, die als Voraussetzung für automatische Generierung der großdimensionalen Prozessgleichungssysteme dienen konnte. Die Bestandteile der obigen Topologien können DSKP und DSVP sein. Die Herleitung der Prozessgleichungen gehört in alle Gegenstandsgebiete zur Forschungsproblematik, welche die neue Wissen in der Form von mathematischen Modellen liefert. In der Abb.1 sind die Gleichungsarten gezeigt: die DSKP werden mit den algebraischen und gewöhnlichen differentialen Gleichungssysteme während die DSVP mit den partiellen Differentialgleichungssysteme beschrieben.

Etappen der parallelen DSKP-, DSVP-Modellierung

Definition 1: Das Modell des komplexen dynamischen Systems ist eine formale KDS-Beschreibung, die notwendige Topologiedarstellung und entsprechende Gleichungssysteme der physikalischen Prozesse beinhaltet und durch die gemeinsamen Vektor-Matrix-Ausdrücke und -Operationen diese Mittel vereinigt (Abb. 1).

Definition 2: Das Simulationsmodell des komplexen dynamischen Systems mit konzentrierten Parametrn ist das umgewandelte DSKP-Modell zur Form, die Anwendung von numerischen Lösungsverfahren erlaubt.

Definition 3: Das Simulationsmodell des komplexen dynamischen Systems mit verteilten Parametrn wird als örtlich diskretisiertes und zur von numerischen Verfahren geforderten impliziten Form umgewandeltes DSVP-Modell definiert.

Wegen der örtlichen Diskretisierung des DSVP ensteht eine sekundäre Topologie, die in der Modellumwandlung eine wichtige Rolle spielt. Die partielle Differentialgleichungssysteme werden durch die gewöhnliche Differentialgleichungssysteme (GDGLS) approximiert. In den DSKP- und DSVP-Simulationsmodellen werden die GDGLS bezüglich der Vektoren von Ableitungen ausgelöst. Die vorhandenen algebraischen Gleichungssysteme werden bezüglich der Vektoren der gesuchten Variablen ausgelöst.

In Abb.2 werden die Etappen der Entwicklung von Modellen der DSKP, DSVP aller genannten Topologien bis zur Umwandlung in den Simulationsmodelle dargestellt [1]. Wegen der DS-Komplexität spielt bei der DSKP- und DSVP-Modellierung die rechnergestützte Erstellung der Topologien, Generierung der Gleichungssysteme sowie ihre Umwandlung in Simulationsmodelle als allgemeines und gegenstandsgebietspezifisches Problem der parallelen Simulationstechnik eine zunehmende Rolle. In Abb.2 wird das Vorhandensein von Mitteln für rechnergestützten Erfüllung entsprechenden Arbeiten vorausgesetzt. Erfahrung zeigt aber, dass diese Mittel in den mehreren Gegenstandsgebiete noch entwickelt werden sollen. Es geht um benutzerfreundlichen simulationsorientierten Bedienoberflächen (BOF), Funktionsalgorithmen und Software der Topologieanalysatoren und Gleichungsgeneratoren.

Die erhaltenen Simulationsmodelle dienen für weitere Schritte der parallelen Simulationstechnik, die mit folgenden Definitionen verbunden sind.

Definition 4: Parallele Modellierung von dynamischen Systemen mit konzentrierten und verteilten Parametern ist ein Vorgang, der zielgerichtet zur Realisierung der obigen DSKP-, DSVP-Simulationsmodelle auf dem vorgegebenen parallelen Rechnersystem führt.

Definition 5: Virtueller MIMD-Prozess ist ein relativ autonomes Programm, das den Lösungsalgorithmus des Gleichungssystemteils realisiert und mit den in der Lösung des Gesamtgleichungssystems beteiligten Prozessen kommuniziert.

Die Körnigkeit des virtuellen Prozesses charakterisiert den Umfang der Berechnungs- und Hilfsoperationen, die im Prozess programmiert werden. Dieser Begriff ist mit der KDS-Dekomposition (Topologie und Modelle) sowie mit der örtlichen DSVP-Approximation verbunden, weil während der Dekomposition bekommen wir die KDS-Einheiten, die in den weiter nicht zerlegbaren Elementen diskretisiert werden. Die DSVP-Ortsdiskretisierung führt zur sekundären VTF-, SAS- und DNO-Topologien, deren Elemente mit entsprechendem System der gewöhnlichen Differentialgleichungen (Differenzgleichungen bezüglich der Ortskoordinate) beschrieben werden. Die Körnigkeit der virtuellen Prozessen wird nach der Betrachtung der Gleichungssysteme aller nach der Dekomposition erhaltenen VTF-, SAS- und DNO-Komponenten und Approximationselementen definiert. Diese Einheiten haben folgende Eigenschaften, die wir für die weitere Parallelisierung in den Betracht nehmen sollen:

• alle Komponenten funktionieren kontinuirlich, also parallel und asynchron zu einander;
• die Ortsdiskretisierung von Komponenten gibt die finite Elemente, die zeitabhängig kontinuirlich bleiben und funktionieren parallel;
• die Kontinuität der Elementen, Komponenten und VTF, SAS und DNO insgesamt bedeutet einerseits eine inhärente Parallelität, verursacht aber andererseits eng gekoppelte Berechnungsprozesse, die auf jedem Zeitschritt einer Datenaktualisierung von Nachbarelementen, Reglern, Energie- und Störungsquellen sowie Knotenverbindungen brauchen.

Die erhaltene Arten von Gleichungen, die die KDS-Komponente und ihre Elemente beschreiben, lassen uns die Körnigkeit von virtuellen Prozessen definieren. Dabei werden wir davon ausgehen, dass die parallelen Rechensysteme die fein- und grobkörnige formale Konstrukte parallel bearbeiten. Die feinkörnige Parallelitätsebene wird durch die einzige Operationen präsentiert, die mit den Anweisungen der jeweiligen Programmiersprachen im SIMD-System mit Hilfe des HOST-Rechners und der Felder von Prozessorenelementen realisiert werden.

Die grobkörnige Parallelelitätsebene wird durch einige Mengen der Operationen präsentiert und dem Prinzip der MIMD-Parallelität entspricht. Dabei ändert sich die im Begriff „Prozeß“ eingebettete Menge der Operationen sehr stark – von des Einanweisungsprogramms bis den recht komplexen Programmen.

Wir werden aus unserer Erfahrung der Aufbau von SIMD- und MIMD-Gleichungslösern ausgehen [2,4,6] und die Perspektive der Realisierung von grobkörnigen Prozessen in den modernen MIMD-Systeme berücksichtigen. Analyse des Caushy-Problems für gewöhnlichen Differentialgleichungen zeigt, dass es sich nicht lohnt, parallel durch Prozesse die Glieder von rechten Seiten der Gleichungen zu berechnen. Als versprechend für weitere Untersuchungen sieht ein Prozess aus, der für die Berechnung der gesuchten Variablen zuständig wäre.

Definition 6 : Die minimalkörnigen virtuellen Prozesse beschränken sich mit den Lösungsoperationen für die Gleichungen, die nach der Dekomposition und der Diskretisierung der VTF-, SAS- und DNO-Komponenten entstanden sind.

Die vorgeschlagene minimale Körnigkeit von Prozessen werden wir für die Erstellung der virtuellen parallelen Simulationsmodelle benutzen.

Definition 7: Virtuelles paralleles DSKP/DSVP-Simulationsmodell (VPSM) ist eine Abstraktion, die aus dem bezüglich den Ableitungsvektoren und den Vektoren der gesuchten algebraischen Unbekannten ausgelösten Gleichungssystem und der nach einem Parallelisierungsansatz entwickelten Struktur der virtuellen MIMD-Prozesse für parallele Lösung der Gleichungssystemteile besteht.

Minimaler Gleichungssystemteil ist eine gewöhnliche Differentialgleichung (oder eine algebraische Gleichung), für deren Lösung ein minimalkörnigen MIMD-Prozess zuständig ist. Für die Realisierung der oben definierten virtuellen Prozesse wählen wir die numerische Verfahren, die in den konventionellen Simulationssprachen Simulink, ACSL u.a. verwendet werden. Für die Untersuchung sind auch die blockartige Verfahren mit interner Parallelität von Interesse.

Die Berechnungen der Vektorelementen nach entsprechenden numerischen Verfahren bedingen den Arbeitsaufwand (den Last) von virtuellen Prozessen. Die VTF-, SAS- und DNO-Gleichungsgeneratoren berücksichtigen die ausgewählte Verfahren und generieren die diskrete virtuelle parallele Simulationsmodelle (DVPSM) der DSKP, DSVP als Berechnungsformeln für gesuchten Variablen der minimalkörnigen Prozesse.

Definition 8: Virtuelles Verbindungsnetzwerk ist abstrakter Schaltautomat, der die logische Verbindungen zwischen den virtuellen MIMD-Prozessen widerspiegelt.

Definition 9: Die virtuelle parallele Rechnerarchitektur ist eine über virtuellen Verbindungsnetzwerk gekoppelte, nach MIMD-Prinzip funktionierte nicht beschränkte Menge der vollfunktionellen Prozessoren, die gemeinsam unter Berücksichtigung des algorithmisch bedingten Datenaustausches das Lösen des Simulationsproblems durchführen.

Definition 10: Das Zielrechnersystem (ZRS) ist die dem Modellentwickler zur Verfügung stehende lose oder/und eng gekoppelte, nach MIMD-Prinzip funktionierte, vorgegebene Menge der installierten vollfunktionellen Prozessoren mit lokalem oder/und gemeinsamem Speicher und verfügbarem vordefiniertem programmgesteuertem Verbindungsnetzwerk.

Definition 11: Paralleler DSKP-, DSVP-Simulator ist vorgegebenes Ziel der parallelen Modellierung und wird als eine Hardware/Software-Systemorganisation definiert, die den Modellierungsvorgang und diskretes virtuelles paralleles Simulationsmodell auf dem Zielrechnersystem sofwaretechnisch effizient realisiert und den Modellentwicklern sowie den Modellanwendern benutzerfreundliche Kommunikation mit den Modellierungs- und Simulationsressourcen erlaubt.

Definition 12: Eine Devirtualisierung des diskreten virtuellen parallelen Simulationsmodells ist eine Umwandlung, die zur Simulatorrealisierung auf gegebenen ZRS eindeutig führt und aus folgenden Grundfunktionen besteht: Apriori-Analyse des DVPSM; Darstellung der vorhandenen ZRS-Ressourcen; Zuordnung “virtuelle Prozesse - reale Prozessoren”, “virtuelles Verbindungsnetzwerk (Kommunikationsgraph) - reales ZRS-Verbindungsnetzwerk” mit der Berücksichtigung von Kriterien der Lastbalancierung, Netzwerkanpassung, Minimierung des Datenaustauschaufwandes; Formierung der Spezifikation von MIMD-Prozessen, die den Prozessoren zugeordnet werden; Formierung des Auftrages für paralleler Code-Generator.

Es wird vorgeschlagen, die parallelen Simulatoren von komplexen DSKP, DSVP entsprechend den in Abb. 3 dargestellten Etappen und Vorgehen der parallelen Modellierung zu entwickeln. Ausgangspunkt der Entwicklung ist eine detaillierte Darstellung und Apriori-Analyse der parallelen virtuellen Simulationsmodelle.

Abb.3. Etappen der parallelen KDS-Modellierung und rechnergestützten Entwicklung von parallelen SIMULATOREN

Die Ziele der Apriori-Analyse sind: ausgehend von minimalkörnigen Prozessen mögliche Ansätze zur Parallelisierung und die strukturelle Darstellungen der DSKP-, DSVP- Parallelitätsebenen zu betrachten; die Parallelitätsebene nach Kriterien Lastverteilung, Datenaustausch, Synchronisation der Prozesse, Rechenaufwand zu prüfen; die möglichen alternativen Lösungen der Organisation von Parallelitätsebenen
vorzuschlagen und zu prüfen; Zusammenfassender Vergleich der Parallelitätsebenen durchzuführen und die Empfehlungen für die Implementierungsarbeiten auf möglichen ZRS zu formulieren.

Die Parallelisierungsansätze werden im Zusammenhang mit der Approximation der DSVP bezüglich der Ortskoordinaten und der Dekomposition von VTF-, SAS- und DNO-Simulationsobjekten auf den weiter nicht zerlegbaren Elemente betrachtet. Die erhaltene VPSM mit minimalkörnigen Prozessen werden wir als paralleles Simulationsmodell der ersten Parallelitätsebene betrachten. Diese Ebene (Abb.3) beinhaltet maximal mögliche Menge der Einheiten „Gleichung - Prozess“ und dient für die Untersuchungen der potentiellen Parallelität von VTF-, SAS-, DNO- und sekundären Topologien. Die Komposition der zerlegten Objekte und eine Gruppierung der minimalkörnigen Prozesse führen zur Betrachtung der höheren Parallelitätsebenen mit der größeren Prozesskörnigkeit und entsprechenden Varianten der Prozess-Prozessor-Zuordnung. Die Apriori-Analyse soll bezüglich aller möglichen Parallelitätsebene vollständig durchgeführt werden und in der Betrachtung folgenden Fragen ihrer Funktionierung bestehen:

• Analyse des Operationenumfanges im virtuellen Prozess;
• Vergleich der Prozesse nach Kriterium „Prozesslasthöhe“;
• Vorschläge zur möglich notwendigen Lastbalancierung;
• Analyse der Kommunikationsoperationen zwischen der Prozessen, Entwicklung des virtuellen Verbindungsnetzwerkes mit minimal möglichem Zeitaufwand für den Datenaustausch.

Weitere Schritte in Abb.3 werden als der Devirtualisierungsvorgang betrachtet [14].

Anforderungen an die Simulationsmitteln

Dynamische Systeme mit konzentrierten und mit verteilten Parametern stellen die folgenden Anforderungen an die Simulationsmitteln [1, 3, 5, 6, 8, 12, 18, 20, 24]:

• Beruecksichtigung der Tatsache, dass die formale Beschreibung komplexer dynamischer Systeme (KDS-Modelle) aus einer Topologiedarstellung sowie der grossdimensionalen Systeme von algebraischen, gewöhnlichen und partiellen Differentialgleichungen besteht [1, 2, 17];
• Benutzerfreundlichkeit: die hochentwickelte Benutzeroberfläche (BOF), rechnerunterstuetzte Modellerstellung und Modelldebugging fuer DSKP, DSVP, die dem Benutzer zur Verfuegung stehende Simulationssprache mit einer domänenabhängigen Modellspezifikation und leichter Erlernbarkeit;
• Hochintellektuelle interaktive Unterstuetzung des Modellentwicklers (Benutzers) auf alle Etappen der Modellierung und Simulation von KDS:
  • Spezifikation der Simulationsobjekte durch die fuer Experten der Gegenstandgebiete klare Sprachmittel; Minimierung des Aufwandes von Routinearbeiten bei der urspruenglichen Beschreibung und Kodierung der KDS-Topologien;
  • Topologische Analyse der Spezifikationen und automatische Generierung der formalen Darstellung von KDS-Strukture und ihren Parametern;
  • Automatische Generierung der KDS-Gleichungssysteme nach Ergebnisse der Topologieanalyse (KDS-Modell) und eine Umwandlung der Gleichungen zur fuer die numerische Lösung geeigneten Form (KDS-Simulationsmodell);
  • Implementierung der von Modellentwickler ausgewählten numerischen Verfahren und Lösung der Gleichungssysteme (KDS-Simulator);
  • Durchfuehrung von Simulationsexperimenten entsprechend dem KDS-Untersuchungsprogramm;
  • Visualisierung und Dokumentierung der Simulationsergebnisse;
  • Archivierung der KDS-Modelle fuer ihre Wiederverwendung;
• Objektorientierte Modellspezifikation fuer Struktur, Verhalten und Parameter von DSKP und DSVP, objektimplementierte Modellierungs- und Simulationssoftware;
• Vorhandensein der Bibliothek von numerischen Verfahren fuer die Modellierung und Simulation der komplexen industriellen DSKP und DSVP;
• Moderne Mittel fuer die Visualisierung und Dokumentation der Modelle, Simulationsmodelle und Simulationsergebnisse;
• Vorhandensein der HW/SW-Ressourcen, die fuer Simulation der real komplexen DSKP, DSVP genuegend sind; Echtzeitfähigkeit zur Kopplung mit den realen DS- und Automatisierungskomponenten (Hardware in-the-Loop);
• Integrationsfähigkeit mit den Werkzeuge fuer die rechnergestuetzte Projektierung von DSKP und DSVP, eine Modellunterstuetzung aller Etappen der KDS-Projekte;
• Eine Systemorganisation der Simulationsressourcen aufgrund der modernen Informationstechnologien;
• Möglichkeit zur Erstellung von anwendungsorientierten Simulationsumgebungen;
• Vorhandensein der Mittel fuer die Schulung von Modellentwicklern und Realisierung der Trainingssimulatoren;
• Integration mit den GRID-Systeme.

Konzeption der verteilten parallelen Simulationsumgebung

Zur Bearbeitung komplexer DSKP-, DSVP-Simulationsaufgaben wird eine verteilte parallele Simulationsumgebung (VPSU) vorgeschlagen, entwickelt und implementiert [1, 2, 4, 12, 14].

Definition13: Die VPSU (Abb.4) definieren wir als eine benutzerfreundliche simulationstechnische Systemorganisation der Hardware, der architekturrelevanten Systemsoftware, der speziell zielgerichtet entwickelten Simulationssoftware sowie der modellierungs-, simulations- und systemtechnischbedingten Subsysteme, mit denen alle Etappen der parallelen Modellierung und Simulation von DSKP, DSVP mit der möglichst vollen Beruecksichtigung der obiegen Anforderungen unterstuetzt werden.

Die VPSU-Entwicklung wird als zentrales Problem der parallelen Simulationstechnik angesehen und von den beteiligten Institutionen nach der folgenden Konzeption durchgefuehrt:

• Beruecksichtigung der DS-Anforderungen an die Simulationsmittel;
• Nutzung der vorhandenen parallelen Ressourcen von SIMD- und MIMD-Architekturen als verteilten Rechensysteme;
• Entwicklung der funktionsvollständigen Simulationssoftware fuer SIMD- und MIMD-Komponenten der VPSU entsprechend den DS-Anforderungen;
• Verwendung von denselben Lösungsalgorithmen fuer DSKP- und diskretisierten DSVP;
• Parallele Simulationssoftware mit ähnlichen Eigenschaften wie bei den vorhandenen block- und gleichungsorientierten Simulationssprachen;
• Problemorientierte VPS-Umgebungen werden als Teilprojekte betrachtet, die allgemeine Lösungen nutzen und Ergebnisse fuer mögliche Verallgemeinerungen liefern;
• VPSU wird als komplexes HW/SW-SYSTEM betrachtet, deren Entwicklung soll auf dem OO-Ansatz mit der UML-Technologie sowie mit der Dekomposition auf bestimmte Menge der Subsysteme erfolgen [6, 14]. Solche Organisation der VPSU-Entwicklung erlaubt nebenläufige Bearbeitung der Teilprojekte (Entwicklungsaufgaben) und eine Erhaltung der Zwischenergebnisse, die zu den arbeitsfähigen Versionen der Simulationsumgebung fuehren.

Abb.4. Systemorganisation der VPSU

Definition 14: Ein VPSU-Subsystem ist eine Teilkomponente der Hardware, Systemsoftware und Simulationssoftware, die benutzerfreundlich eine gewisse Gruppe von inhaltlich nahen Funktionen auf entsprechenden DSKP/DSVP-Modellierungs- und Simulationsetappen erfuellt.

Unsere Realisierungserfahrung der SIMD- und MIMD-Komponenten von VPSU bestätigt die Produktivität und Entwicklungsperspektive vorgeschlagener Konzeption. Es wurden die Struktur der VPSU mit SIMD-HARDWARE MasPar sowie der DSKP- und DSVP-Simulationssoftware mit parallelen Programmiersprache PARALLAXIS vorgeschlagen, begruendet und erprobt [2, 4, 6]. Fuer DSKP wurden in konventionellen Simulationssprachen vorhandene Algorithmen parallelisiert und in Richtung der Topologieanalyse und Gleichungsgenerierung weiterentwickelt. In [4] ist die Analyse der DSKP-SIMD-Algorithmen dargestellt. Es wurde die Benutzeroberfläche mit der verschiedenen Ansätze zur Modellerstellung sowie problemorientierte SIMD-VPSU [6] untersucht. Die SIMD-Erfahrung wird mit den Anwendungsperspektiven von CUDA-Ansätze [21] aktualisiert.

Die vorgeschlagene VPSU wird von HLRS und FRTI nach Abb.5 realisiert, implementiert und experimentell untersucht [11, 13, 14, 15, 20].

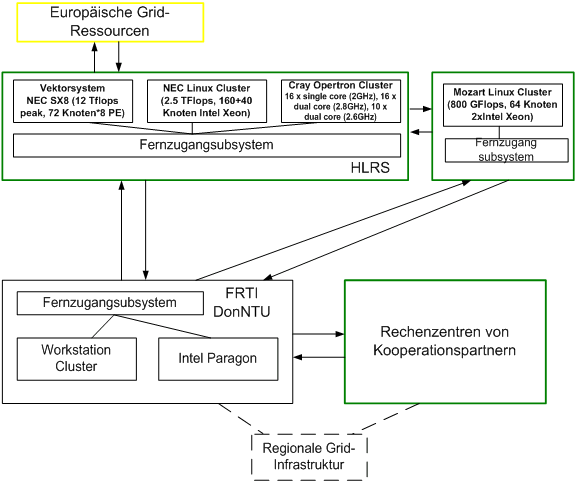
Abb.5. Aktuelle VPSU-Hardwarestruktur

Problem der Entwicklung von VPSU-Simulationssoftware

Die Hauptbestandteile der VPSU-Simulationssoftware sind in Abb.4 dargestellt. Die Funktionalität dieser zugrundeliegenden Komponente der Simulationsumgebung wird von in Abbildungen 2, 3 zusammengefassten Etappen der parallelen Modellierung und Simulation von komplexen dynamischen Systemen bedingt. Das Problem der vollfunktionellen Entwicklung der VPSU-Simulationssoftware wird mit Hilfe der Verteilung der gesamten Funktionalität zwischen folgenden Subsystemen gelöst:

1. Dialogsubsystem (DiSuS, die Benutzeroberfläche — BOF) — eine Präsentation der VPSU; Schulung von Benutzern; aktives Dialog der Modellentwickler mit alle Ressourcen des verteilten Rechnersystems; Integration mit alle anderen Subsystemen; Anpassung an die Simulationsaufgaben der Gegenstandsgebiete; Planung und Fuehrung der Simulationsexperimente.
2. Topologieanalysesubsystem (TASuS) — verbale und grafische Darstellung sowie geeignete Kodierung von urspruenglichen VTF-, SAS-, DNO-Topologien; Dekomposition und Aproximierung, Erstellung der sekundären Topologien; Formierung der topologierelevanten Vektoren und Matrizen; Umwandlung der urspruenglichen Kodierungstabellen in die Zwischenformen; Darstellung der topologischen Informationseinheiten in der fuer die Gleichungsgenerierung geeigneten Form; eine Ausgabe der Topologieanalyseergebnissen.
3. Subsysten der Gleichungsgenerierung (SuGG) — Kommunikation mit dem TASuS; Darstellung der urspruenglichen Gleichungen (Modelle) in Vektormatrixform; formale Vektor-Matrix-Operationen der Umwandlung "DSKP-Modell — Simulationsmodell"; Darstellung der approximierten DSVP-Gleichungen (1D-, 2D-, 3D-ortsdiskretisierten Modelle) in der Multivektor-Matrix-Form; die formale Umwandlung "DSVP-Modell — Simulationsmodell"; die Generierung von diskreten DSKP-, DSVP-Simulationsmodelle fuer gegebenes numerisches Lösungsverfahren; die Visualisierung der Modelle und Simulationsmodelle.
4. Subsystem der virtuellen parallelen Simulationsmodelle (VPSMSu) — interaktive Darstellung der Hierarchie von virtuellen parallelen Simulationsmodelle abhängig von möglichen Parallelisierungsansätze; TASuS-gestuetzte Erstellung der Topologien entsprechend den VPSM-Ebenen; SuGG-unterstuetzte Formierung der VPSM-Ebene-Gleichungssysteme; Apriori-Analyse der diskreten VPSM aller Ebenen; interaktive Bereitstellung von implementierungsfähigen diskreten VPSM.
5. Subsystem von parallelen Gleichungslösern (SuPaGL) — Kommunikation mit dem TASuS und VPSMSu, die Eingabe der implementierungsfähigen diskreten VPSM; die Lösung von algebraischen, gewöhnlichen und partiellen Differentialgleichungssysteme mit Hilfe der in den DSKP-, DSVP-Bibliotheken zusammengefassten parallelen numerischen Verfahren; die Analyse der Konvergenz, Stabilität und Genauigkeit der Lösungen, Optimierung der varriirten Parametern; Abschätzung und Optimierung der Effizienzmerkmalen von parallelen Lösungen in Vergleich mit den sequentiellen Verfahren; Formierung der Lösungsergebnisse fuer die anschaulichen Präsentation.
6. Datenaustauschsubsystem (DASu) — die vollfunktionelle Liste der angemeldeten VPSU-Teilnehmern und vorhandenen VPSU-Ressourcen, die ein Datenaustausch nach gemeinsame Initiative durchfuehren sollen; eine Hierarchiedarstellung von Datenströme fuer ausgewählten ZRS; Testsystem fuer die Ermittlung der realen Parametern von Austauschoperationen im ZRS-Verbindungsnetzwerk; Optimierung der parallelen Programme bezueglich der Datenaustauschoperationen; Zusammenstellung der in der Apriori-Analyse und im ZRS erhaltene Wirkung der DA-Operationen auf die Werte der Effizienz von Parallelisierungsansätzen.
7. Lastbalancierungssubsystem (LaBSu) — Abschätzung der Lasthöhe von virtuellen Prozessen in VPSM-Ebenen, statische Lastbalancierung der VPSM aller Ebenen; Spezifikation der Aufträge auf VPSU-Ressorcen von implementierten VPSM; eine Ermittlung der Lastverteilung zwischen Prozessen und zwischen ZRS-Prozessoren; Vergleichsanalyse der Parallelisierungsansätze nach Kriterium der gleichmässigen Lastverteilung.
8. isualisierungssubsystem (ViSuS) — in Integration mit BOF und Subsystem von Gleichungslösern eine Vorbereitung und Strukturierung der Simulationsergebnissen zu den Formen, die fuer grafischen 1D-, 2D- und 3D-Visualisierung geeignet sind; interaktive Erstellung von Grafiken während und nach der Durchfuehrung von Simulationsexperimenten.
9. Datenbanksubsystem (DaBSu) — in der Integration mit allen anderen Subsystemen: Daten ueber VPSU-Hardware und Systemsoftware; Benutzerdaten; urspruengliche und umgewandelte Daten der modellierten VTF-, SAS- und SNO-KDS; Archivierung der lauffähigen parallelen und sequentiellen Programme; Daten der Testaufgaben, Pläne der Simulationsexperimenten, Archivierung der Simulationsergebnissen.
10. Subsystem der IT-Unterstuetzung (SuIT) — Betriebsorganisation von verteilten Rechen-, Kommunikations- und Simulationsressourcen durch die Technologien der modernen Netzwerke; entfernter WEB-basierter Ansatz zur parallelen Modellierung und Simulation; Funktionierung der Ketten "WEB-Client (Modellentwickler) – WEB-Server – PARSIMULATOR" und "WEB-Client (Modellentwickler) – WEB-Server – DATABASE-Server"; Integration mit anderen Subsystemen.

Die vollfunktionelle DSVP-Simulationssoftware soll die in Abb.6 gezeigten Module beinhalten. Sie entsprechen den Etappen der parallelen DSVP-Modellierung und Simulation (Abb.2, 3) und der obigen Anforderungen an die Modellierungs- und Simulationsmitteln. DSVP-Bibliothek stellt dem Benutzer die parallelen numerischen Lösungsverfahren der partiellen Differentialgleichungen der genanten Typen zur Verfuegung. Die DSKP-Simulationssoftware besitzt eine ähnliche Struktur. Die parallele numerische Verfahren fuer Lösung der gewöhnlichen Differentialgleichungen werden in DSKP-Bibliothek zusammengefasst und mit DSVP-Bibliothek integriert, weil die Dekomposition und Ortsdiskretisierung von DSVP zu den grossdimensionalen Systeme der gewöhnlichen und algebraischen Gleichungen fuehrt.

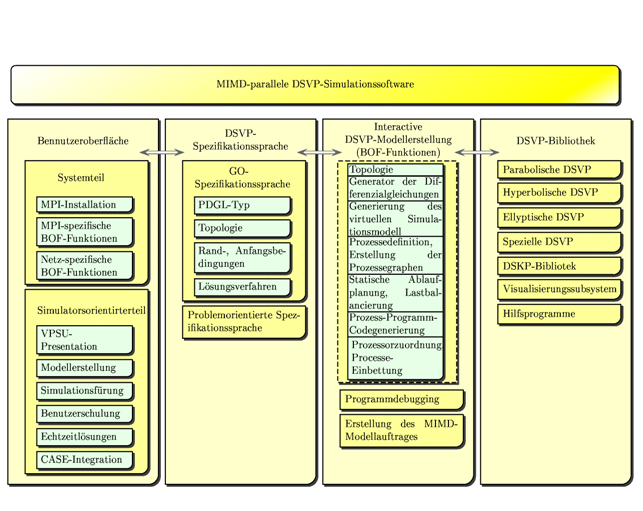
Abb.6. Struktur der MIMD-Simulationssoftware fuer dynamische Systeme mit verteilten Parametern

Die in obigen Bibliotheken eingebetteten parallelen Gleichungslösern werden nach folgenden Ansätzen entwickelt:

1. Eine Parallelisierung der numerischen Verfahren, die in den benutzerfreundlichen konventionellen Simulationssprachen erfolgreich verwendet werden (Euler, Adams-Bashforth, Runge-Kutta u.a. Verfahren). Diskrete Form der minimalkörnigen Prozesse und virtuellen parallelen Simulationsmodelle ist durch die Berechnungsformeln dieser Verfahren definiert.
2. Entwicklung der neuen parallelen Lösungsverfahren [6].

Fuer die gewöhnlichen Differentialgleichungssysteme entwickeln wir die blockartigen Verfahren, welche fuer einen Block von k Punkten berechnen die neue k Funktionswerte gleichzeitig. Diese Verfahrenseigenschaft passt gut zur parallele Rechnerarchitekturen und erlaubt die Berechnungen von Koeffizienten der Differenzformeln vor der Integrierung, schon während der Entwicklung des Verfahrens und erhöht die Effizienz des Rechnens. Betrachten wir die Lösung des Caushy-Problems

mit Hilfe des blockartigen k-Punktverfahrens (Abb. 7). Zerlegen wir dabei die Knotenmenge М des homogenen Gitters {tm}, m = 1,2,…, M mit dem Schritt auf Blöcke, die je k Punkte beinhalten, kN>M. Numerieren wir in jedem Block die Punkte i = 0,1,…, k und bezeichnen als tn,i den Punkt i des n-ten Blocks. Die Punkte tn,0 und tn,k sind entsprechend der Anfang und das Ende des Blocks n. Daraus folgt, dass tn,k = tn + tn,0, dabei wird der Anfangspunkt dem Block nicht gehören.

Abb.7. Schema der Zerlegung auf die Blöcke

Wir werden zwischen den blockartigen Einschritts- und Mehrschrittsverfahren unterscheiden (Abb. 8, 9).

Abb.8. Berechnungsschema beim blockartigen Einschrittsverfahren

Abb.9. Berechnungsschema beim blockartigen Mehrschrittsverfahren

Im allgemeinen Fall haben die Gleichungen fuer das m-schrittliche k-punktliche blockartige Verfahren folgende Form:

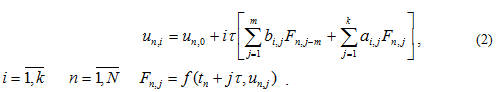
Es wurden die ausfuehrlichen theoretischen Untersuchungen der blockartigen Ein- und Mehrschrittsverfahren bezueglich der Konfergenz- und Stabilitätanalyse, der Fehlerabschätzungen durchgefuehrt [7, 9, 17]. Es wurde festgestellt, dass die zweischrittlichen zweipunktlichen und vierschrittlichen vierpunktlichen blockartigen Verfahren А(a) — stabil bei beliebigem a nicht können sein. Deshalb sind diese Vefahren fuer die Lösung der staufen Gleichungssysteme nicht geeignet. Es wurde das parallele blockartige eingebettete und extrapolierende Verfahren aufgrund der impliziten Einschrittverfahren fuer die beschleunigte Lösung der staufen Gleichungen vorgeschlagen und begruendet. Die hergeleiteten analytischen Ausdruecke fuer die Abschätzung der Beschleunigung, Effizienz und Skalierbarkeit der parallelen blockartigen Ein- und Mehrschrittsverfahren wurden auf Testaufgaben erprobt. Diese Ergebnisse stellen zuverllässiger Grund fuer die weiteren Entwicklung und Realisierung paralleler Gleichungslösern dar.

Problemorientierten parallelen Simulationsumgebungen

Entwicklung der problemorientierten VPSU bleibt als aktuelle Herausforderung in verschiedenen Gegenstandsgebiete [1, 5, 6, 8, 11, 14]. Wissenschaftliche und praktische Bedeutung haben folgende Aufgabenlösungen: die Spezifikationssprachen der DSKP, DSVP auf technologischer Ebene; die formale Beschreibung von Topologien und physikalischen Prozessen, Algorithmen der Topologieanalyse und der Gleichungsgenerierung; die Ansätze zur Parallelisierung, Entwicklung der virtuellen parallelen Simulationsmodelle und ihre theoretische Analyse; Devirtualisierung und Prozessezuordnung auf ZRS, Anpassung der numerischen Verfahren und Aufbau von parallelen Gleichungslösern; Entwicklung der effektiven Subsysteme; Effizienzanalyse und Optimierung der parallelen Simulatoren; Integration mit der gegenstandgebietspezifischen CASE-Werkzeuge, modellgestuetzte Projektierung und Prozessfuehrung; benutzerfreundliche Systemorganisation der Anwendung von parallelen Ressourcen.

Simulationsumgebung fuer dynamische Netzobjekte (DNO-Topologie)

Die dynamische technische und verfahrenstechnische Netze sind in mehreren Gegenstandsgebiete die Objekte der Untersuchung, Projektierung, Automatisierung, ueberwachung, Qualitätssicherung, optimalen Prozessfuehrung, Sicherheitsanalyse und -vorhersage, Vermeidung der sicherheitskritischen Betriebzustände und der Havarieliquidierung. Die Netzobjekte gehören zu den komplizierten (oft sicherheitskritischen) dynamischen Systemen. Nichtlinearität der prozessbeschreibenden Funktionen, räumliche Verteilung von Prozessparametern, grosse, im Laufe des Objektbetriebs sich entwickelnde Dimensionen der Netze (Kantenmenge m>100, Knotenmenge n>50), ebenso mehrere aktive Elemente mit nichtlinearen stromabhängigen Charakteristiken, wesentliches mehrfaches und hierarchisches Zusammenwirken der regelbaren Prozessparametern, sowie gleichzeitige Einfluesse von deterministischen und stochastischen Störungen sind die Hauptmerkmale dieser Komplexität. Nur wenige, sehr vereinfachte Aufgaben der dynamischen Netzobjekte kann man jedoch analytisch lösen. Deshalb haben die Methoden und Mittel der Modellierung und Simulation dieser Objektklasse sowohl bei der Projektierung als auch während des Betriebes eine zunehmende theoretische und praktische Bedeutung. In Abb. 10 werden die Dekomposition des Grubenbewetterungsnetzes und Diskretisierung der Luftwege (Kanten des Netzgraphen) erläutert.

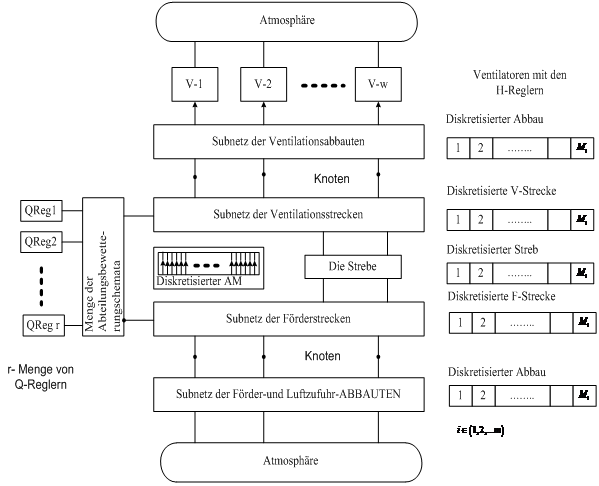
Abb.10. Dekomposition und Diskretisierung des dynamischen Netzobjektes

Die minimalkörnige Prozesse (4) entstehen aus der nach Linienverfahren approximierten partiellen Differentialgleichungen (3), die den Luftstrom Qj und Druck Pj im j-Graphenkante beschreiben:

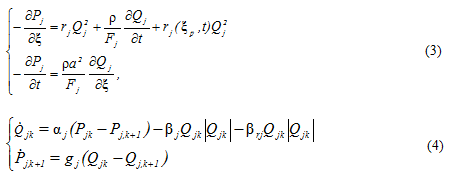
generiert. Hier sind PU = (PU1,PU2,…,PUn-1)T – Druckvektor der Knoten, G – diagonale Matrix der Parametern g der den Knoten inzidenten Kanten.

Die Parallelisierungsansätze geben vier möglichen Parallelitätsebenen des virtuellen parallelen Simulationsmodells (Abb.11).

Es wurde paralleler DNOVP-Simulator (Abb.12) [10, 11, 13]entwickelt, implementiert und im Simulations- und Servicezentrum fuer die Kohleindustrie [12] experimentell untersucht.

Verfahrenstechnisch orintierte parallele Simulationsumgebung

Basierend auf der Entwicklungserfahrung von universellen und problemorientierten parallelen Simulationsumgebungen fuer dynamische Systeme mit konzentrierten und verteilten Parametern [1, 2, 4, 6, 11, 14], der Entwicklung und Realisierung der Modellierungs-systematik von verfahrenstechnischen Prozesse und Anlagen (VTPA) in dem Simulationssystem DIVA und im Werkzeug PROMOT [1, 5], einer Analyse der Simulationsstrategien und modularen Simulationsansätze in der Verfahrenstechnik [1, 5] wird eine verteilte verfahrenstechnisch orientierte parallele Simulationsumgebung (VTOPSU) vorgeschlagen.

VTOPSU entspricht der Definition 13 und wichtige Eigenschaften der Verfahrenstechnik als des Gegenstandsgebietes beruecksichtigt. Abb. 13 zeigt die Strukturdarstellung der VTOPSU. Zur Zeit ist eine Versuchsversion der Umgebung realisiert und am Beispiel der Modellierung und Simulation der Essigsäureproduktion erprobt [16].

Abb.11. Die virtuellen Parallelitätsebenen des parallelen DNOVP-Simulationsmodells

Abb.12. Struktur des DNO-Simulators

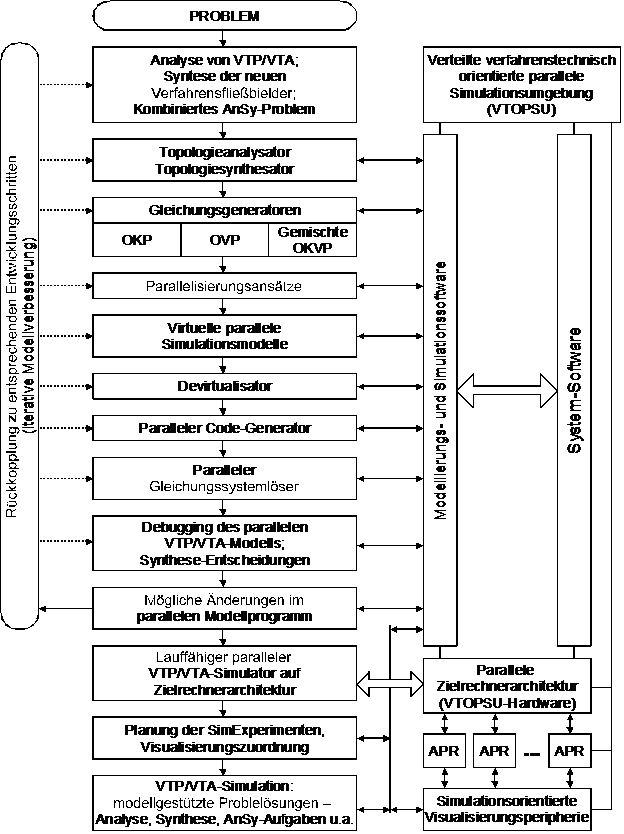
Abb.13. Strukturdarstellung der VTOPSU

Die vorgesehene VTOPSU-Funktionalität umfasst die rechnergestuetzte dialogbasierte Lösung folgenden Aufgabenblöcke bei der parallelen Modellierung und Simulation von verfahrenstechnischen Prozessen und Anlagen:

• Darstellung der VTP/VTA-Topologie, eine Generierung der topologiebediengten Gleichungssysteme in der von numerischen Lösungsverfahren geforderten Form;
• Erstellung der virtuellen parallelenVTP/VTA-Simulationsmodelle mit der Beruecksichtigung der alternativen Parallelisierungsansätze;
• Aproiri-Analyse und Devirtualisierung der Simulationsmodelle und ihre Zuordnung auf parallelen Zielrechnersystem;
• Generierung des parallelen Programmcodes fuer dem ZRS zugeordnetes Simulationsmodell;
• Initialisierung, Parameterzuweisung und Debugging der parallelen VTP/VTA-Simulationsmodelle, ihre iterative Qualitätsverbesserung;
• Effektive parallele Lösung der fuer die VTP/VTA-Simulationsmodelle relevanten Gleichungssysteme mit der Visualisierung der erhaltenen dynamischen Verhalten von Prozessen und Anlagen;
• Aufbau der parallelen VTP/VTA-Modellbibliothek, die Wiederverwendung der parallelen Simulationsmodelle, Realisierung der verfahrenstechnischen Modellierungssystematik in den heterogenen örtlich verteilten Rechnernetze.

Problem der Entwicklung von parallelen Simulationssprachen

Die Benutzerfreundlichkeit der parallelen Rechnersysteme ist in ersten Reihe mit den vorhandenen Programmiermodelle und Mitteln fuer Realisierung der parallelen Lösungsalgorithmen verbunden. Die Systeme der 90-zigen Jahren verfuegten ueber parallele SIMD- und MIMD-Programmiersprachen, die aufgrund von Fortran, C, C++, Modula-2 u. a. Sprachen gebaut wurden [2]. Intensive Entwicklung der MIMD-Systeme und objektorientierten Ansätze hat die Standartisierung der Technologien der parallelen und verteilten Programmierung stimuliert. So haben die ANSI, ISO C++-Standard mit den MPI-, PVM- und Pthreads-Bibliotheken eingefuehrt. Trotz gewisse Fortschritt soll Gegenstandsexperte (Modellentwickler) heute wie frueher mit der Programmiersprache die parallele Modelle realisieren und damit auf dem Niveau der ehemaligen konventionellen Simulationssysteme der zweiten und dritten Generation [3] bleiben. Diese Tatsache beschränkt wesentlich eine Nutzung der parallelen Ressourcen von Fachleute, die mit den block- (BO), gleichungs- (GO) und objektorientierten (OO) Simulationssprachen [3, 10] dynamische Systeme modellieren und simulieren. Um VPSU zu den Simulationsmitteln etwa der fuenften Generation [3] einzunäheren, sollen wir die parallele Simulationssoftware in Richtung parallelen Simulationssprachen weiter zu entwickeln. Diese Sprachen sollen eindeutige Verbindung zwischen den Gegenstandsgebiete der verfahrenstechnischen Ebene und den formalen Beschreibung von dynamischen Systemen (Abb.1) mit Hilfe der Modellspezifikation benutzerfreundlich widerspiegeln und in den lauffähigen parallelen Simulatoren umwandeln (Abb.2,3). Analyse zeigt, dass die VTF-, SAS- und DNO-Topologien allgemein in Graphendarstellung umgewandelt werden können. Die entwickelten und experimentell untersuchten Paare „Topologieanalysatoren — Gleichungsgeneratoren“ geben die Simulationsmodelle, die direkte Anwendung der BO- und GO-Prinzipien der Gleichungslösung erlauben, ohne die diskrete Simulationsmodelle zu generieren. Dabei sind die folgenden Ideen der BO- und GO-Ansätze zu beachten.

BO-Lösungsprinzip entspricht der MIMD-Parallelität und kann als eine virtuelle Zuordnung „Funktionsblock – Prozess“ betrachtet werden. Dem minimalkörnigen Prozess soll eine Funktionsblockkette zugeordnet werden, die eine Differentialgleichung der ersten Ordnung löst. Diesen Ketten werden vom Generator des BO-Lösers nach entwickelten Algorithmen erstellt. So entsteht die von dem BO-Lösungsprinzip bedingte virtuelle Blockschaltung, die das virtuelle parallele Simulationsmodell der ersten Parallelitätsebene (PE-1) mit minimal körnigen Prozessen (MKP) „realisiert“. Das virtuelle Verbindungsnetzwerk (VNW) hat zwei Ebene: innere MKP-Verbindungen sowie äussere, die alle MKP entsprechend der Approximationschema verbinden. Der Devirtualisierungsvorgang wird vom vorgeschlagenen in der VPSU-Simulationssoftware (Abb.3) eingebauten BO-Devirtualisator durchgefuehrt. Als Randbedingungen hat er PE-1 und ZRS. Die optimale Zuordnung dem ZRS wird mit der Beruecksichtigung der höheren Parallelitätsebenen etwa PE-2 – PE-4 und der Abbildung ihren virtuellen VNW-2 – VNW-4 in dem ZRS-Verbindungsnetwerk realisiert. Diese Zuordnung benutzt Code-Generator, der ein lauffähiges MPI-Programm produziert.

GO-Lösungsprinzip basiert sich auf der Darstellung der Simulationsmodelle in Form von Funktionsoperatoren, die als feinkörnige Prozesse betrachtet werden können. Es gibt auch die komplexen Operatoren, die fuer die Lösung der Differentialgleichungen der 1.Ordnung zuständig sind und dem oben eingefuehrten minimalkörnigen MIMD-Prozess entsprechen. GO-Ansatz braucht deshalb eine zusätzliche Funktion in den obigen Gleichungsgeneratoren (Abb.3): „Umwandlung des Simulationsmodells in GO-Form“. Als Ergebnis wird virtuelles paralleles GO-Simulationsmodell PE-1 sein. Virtuelles Verbindungsnetzwerk ist mit obigen äusseren BO-Variant ähnlich und realisiert die Verbindungen zwischen den GO-Operatoren-MPK entsprechend der DSVP-Approximation. Wie im BO-Ansatz sollen hier der GO-Devirtualisator und der Code-Generator entwickelt und eingebaut werden.

Objektorientierter Ansatz ist aufgrund der vorhandenen OO-Simulationssprachen [10] mit der Beruecksichtigung von obigen beiden Ansätzen realisierbar.

Zusammenfassung und Ausblick

Die vorgestellten Ergebnisse liefern einen Beitrag zum aktuellen Forschungsthema der parallelen Simulationstechnik fuer die Untersuchung komplexer Modelle von örtlich konzentrierten und verteilten Systemen (DSKP und DSVP). Dabei wurden die folgenden Probleme schwerpunktmässig untersucht:

• Simulationstechnisch effiziente Nutzung von parallelen Harware- und Software-Ressourcen: Die vorgeschlagene Konzepte der allgemeinen und problemorientierten parallelen Simulationsumgebungen sowie ihre Implementierungen erfordern eine neue Systemorganisation der parallelen Simulationsmitteln.
• Erhöhung der Benutzerfreundlichkeit von parallelen Simulationswerkzeugen: Die vorgeschlagene Topologieanalysatoren und Gleichungsgeneratoren fuer dynamischen Netzobjekte können in verschiedenen Anwendungsgebieten eingesetzt werden.
• Rechnergestuetzte Modellierung und parallelen Simulationund von DSKP und DSVP: Mit Hilfe der vorgestellten virtuellen Simulationsmodelle und Devirtualisierungsvorgänge erfolgt eine Systematisierung der einzelnen Entwicklungsschritte.
• Entwicklung von parallelen Simulationsalgorithmen fuer DSKP und DSVP: Die entwickelten Gleichungslöser sind aufgrund der konventionellen und parallelen numerischen Verfahren wichtige Bestandteile der parallelen Simulations-umgebungen.
• Implementierung und Einsatz von problemorientierten parallelen Simulations-umgebungen: Die untersuchte PSU-Dekomposition auf funktionelle Subsysteme erlaubt eine parallele system- und programmtechnische PSU-Entwicklung.
• Entwicklung von parallelen Simulationssprachen fuer die erweiterte Anwendung von parallelen Rechnern und der modellgestuetzten Projektierung von DSKP und DSVP: Die betrachteten Ansätze erlauben den kontinuierlichen uebergang von vorhandenen standardisierten Sprachen und Bibliotheken auf die höheren Sprachen der parallelen Modellierung und Simulation.
• Integration der Methoden und Werkzeugen der parallelen Simulationstechnik mit der Theorie und Praxis von verteilten Systemen und modernen IT-Lösungen: Die Implementierungserfahrungen mit einer räumlich verteilten parallelen Simulationsumgebung und ein effektiver Fernzugriff auf verschiedene Parallel-rechner bilden eine Basis fuer experimentelle Untersuchungen in dieser Richtung.

Die weiteren Forschungsarbeiten zur parallelen Simulationstechnik konzentrieren sich auf parallele Simulationsalgorithmen, objektorientierte Ansätze, problemorientierte Umgebungen sowie auf industrielle und universitäre Anwendungen.

Literatur

1. Zeitz, M.: Simulationstechnik.Chemie-Ingenieur-Technik 59 (1987), 464-469
2. Anoprienko A.J., Svjatnyj V.A., Bräunl T., Reuter A., Zeitz M.: Massiv parallele Simulationsumgebung fuer dynamische Systeme mit konzentrierten und verteilten Parametern. Tagungsband 9. Symposium ASIM’94, Vieweg, 1994, 183-188.
3. Schmidt B.: Simulationssysteme der 5. Generation. SiP, Heft 1, 1994, 5-6.
4. Feldmann L.P., Lapko V.V., Svjatnyj V.A., Trub I. I., Bräunl T., Reuter A., Zeitz M.: Algorithmen einer massiv parallelen Simulationsumgebung fuer dynamische Systeme mit verteilten Parametern. Tagungsband 10. Symposium ASIM’96, Vieweg, 1996, 519-524.
5. Gilles, E.-D.: Modellierungssystematik fuer verfahrenstechnische Prozesse. In: Abschlussbericht "Methoden zur Modellierung und Berechnung der Dynamik verfahrenstechnischer Prozesse" der DFG-Forschergruppe Universität Stuttgart, 1996, 7-22.
6. Feldmann L.P. Svjatnyj V.A., Bräunl T., Reuter A., Zeitz M.: Implementierung und Effizienzanalyse der parallelen Simulationsalgorithmen fuer dynamische Systeme mit verteilten Parametern (Plenarvortrag). Tagungsband 11. Symposium ASIM’97, Vieweg, 1997, 38-47.
7. Feldmann L.P. Implementierung und Effizienzanalyse von parallelen blockartigen Simulationsalgorithmen fuer dynamische Systeme mit konzentrierten Parametern. Tagungsband 14. ASIM-Symposium Simulationstechnik, Hamburg 2000, SCS-Europe BVBA, Ghent/Belgium 2000, 241-246
8. Borchard J.: Newton-type decomposition methods in large-scale dynamic process simulation. In: Computers and Chemical Engineering, 25 (2001), 951-961.
9. Feldmann L.P., Dmitrieva O.A., Gerber S.. Abbildung der blockartigen Algorithmen auf Parallelrechnerarchitekture. Tagungsband 15. ASIM-Symposium Simulationstechnik, Rostock 2002, SCS-Europe BVBA, Ghent/Belgium 2002, 359-364.
10. Modelica – A Unified Object-Oriented Language for Physical Systems Modeling. Language Specification. Version 2.0, 2002.
11. Svjatnyj V.A., Moldovanova O.V., Cheptsov O.O., Rothermel K., Zeitz M. Generierung und parallele Lösung von Simulationsmodellen fuer Netzobjekte mit verteilten Parametern. Tagungsband 17. ASIM-Symposium Simulationstechnik, Magdeburg 2003, SCS 2003, 193-198.
12. Svjatnyj V.A., Moldovanova O.V., Feldmann L.P.: Parallele Simulationsumgebung fuer dynamische Netzobjekte mit verteilten Parametern. Tagungsband 18. ASIM-Symposium Simulationstechnik, Erlangen 2005, SCS 2005, 416-421.
13. Svjatnyj V., Beljaev O., Lapko V., Tschepzov O., Hohmann R.: Zur Entwicklungsorganisation des Simulations- und Servicezentrums fuer die Kohleindustrie. Tagungsband 18. ASIM-Symposium Simulationstechnik, Erlangen 2005, SCS 2005, 554-559.
14. Moldovanova O.V., Svjatnyj V.A., Feldmann L., Resch M., Kuester U.: Problemorientierte parallele Simulationsumgebung. In: DonNTU, FRTI-Werke, Reihe “Informatik, Kybernetik und Rechentechnik”, Band 93. – Donezk 2005, 145–150.
15. Svjatnyj V., Moldovanova O., Smagin A., Resch M., Keller R., Rabenseifner R.: Virtuelle Simulationsmodelle und ein Devirtualisierungsvorgang fuer die Entwicklung der parallelen Simulatoren von komplexen dynamischen Systemen. In: DonNTU, FRTI-Werke, Reihe “Probleme der Modellierung und rechnergestuetzten Projektierung von dynamischen Systemen”, Band 5(116). – Donezk 2006, 36–43.
16. Bondareva, K., Svjatnyj, V.: Verfahrenstechnisch orientierte parallele Simulationsumgebung. In: DonNTU, FRTI-Werke, Reihe “Probleme der Modellierung und rechnergestuetzten Projektierung von dynamischen Systemen”, Band 5(116). – Donezk 2006, 28–35.
17. Feldmann, L.P., Nasarova, I.A.: Parallele Algorithmen der numerischen Lösung von Caushy-Aufgabe fuer gewöhnlichen Differentialgleichungssysteme. In: Mathematische Modellierung, Band 18, N6, 2006, S. 17-31. (Russisch)
18. Michael M. Resch and Uwe Kuester: Future Challenges in Supercomputing. In: PIK Praxis der Informationsverarbeitung und Kommunikation, PIK 29 (2006), 214 – 220.
19. Edgar Gabriel, Feng Sheng, Rainer Keller, and Michael Resch: A Framework for Comparative Performance Analysis of MPI Applications. In: The 2006 International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA’06), Las Vegas/USA, 2006.
20. Boenisch Th., Alessandrini V.: DEISA overview: projekt status, strategies and perspectives. In: Sixth DEISA Training Session, HLRS, Stuttgart, 2008, 1-49.
21. Nickols, J., Buck, I., Gerland, M. Scalable Parallel Programming with CUDA. ACM Queue,6, 2, 2008, 40-53
22. W. E. Nagel, D. B. Kröner, M. Resch (Eds.), High Performance Computing in Science and Engineering 08, Transactions of the High Performance Computing Center Stuttgart, Springer, Berlin – Heidelberg - New York, 2008.
23. S.R. Tiyyagura, P. Adamidis, R. Rabenseifner, P. Lammers, S. Borowski, F. Lippold, F. Svensson, O. Marxen, S. Haberhauer, A.P. Seitsonen, J. Furthmueller, K. Benkert, M. Galle, T. Boenisch, U. Kuester, M.M. Resch: Teraflops - Sustained Performance with Real World Applications. In: International Journal of High Performance Computing Applications, Volume 22 (2), 131 – 148, 2008.
24. Edgar Gabriel, Katharina Benkert, Michael M. Resch: Towards Performance and portability through Runtime Adaption for High Performance Computing Applications. In: ISC‘2008, Dresden/Germany, 2008.