Назад в библиотеку
Отбор регрессионных моделей для прогнозирования потери крови при родах с помощью ГА
Автор: Т.А. Васяева, М.А. Пачаджи
Источник: Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС КМ – 2012) – 2012 / Матерiали II мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк: ДонНТУ, 2012. – № 2. – 132–136 с.
Аннотация
М.А. Пачаджи, Т.А. Васяева Отбор регрессионных моделей для прогнозирования потери крови при родах с помощью ГА. Рассмотрены системы блочного моделирования. Исследовано моделирование уравнения гармонического осциллятора. Проведено сравнение моделирующих сред.
Введение
Ежегодно в мире при родах и в послеродовом периоде умирает 350–370 женщин. Самая частая причина смертности – акушерское кровотечение.
Акушерские кровотечения являются одним из самых опасных осложнений, которые могут произойти во время родов, частота их появления 2–3% из всех случаев.
Возможность прогнозирования патологической акушерской кровопотери накануне родов позволит своевременно создать запасы кровезаменителей, плазмы, препаратов
крови, возможно и аутокрови, а также оказать адекватную терапию с привлечением высококвалифицированных реаниматологов, акушеров-гинекологов и сосудистых
хирургов для проведения органосохраняющих операций(перевязка сосудистых пучков и подчревных артерий) в случае развития послеродового кровотечения.
Общая постановка проблемы
При построении математической функции классификации или регрессии основная задача сводится к выбору наилучшей функции из всего множества вариантов.
Дело в том, что может существовать множество функций, одинаково классифицирующих одну и ту же обучающую выборку (рис. 1).
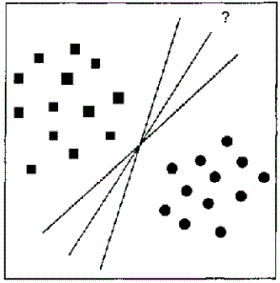
Рисунок 1 – Варианты линейного разделения обучающей выборки
Для построения регрессионной модели необходимо выполнить отбор необходимых факторов и затем рассчитать коэффициенты уравнения. Естественно выбирая тот или иной набор параметров можно получать различные
регрессионные модели, причем многие из них будут показывать хорошие результаты.
Таким образом, для построения оптимальной модели необходимо решить две задачи: выбрать факторы риска, которые будут переменными множественной регрессии; и рассчитать коэффициенты уравнения.
Отбор факторов риска является непростой задачей [2], которую можно решать с помощью ГА [3]. Предлагается решать эти две задачи одновременно.
Разработка метода
Стандартный ГА [1, 2] предполагает следующую последовательность, (рис.2).

Рисунок 2 – Простой генетический алгоритм
- На первом этапе выполняется генерация начальной популяции, где случайным образом генерируется некоторое количество особей. Важным этапом является разработка способа кодирования хромосомы, так как каждая особь это возможное решение задачи (уравнение множественной регрессии).
Мы предлагаем следующую структуру хромосомы, (рис. 3). Каждая особь представляется последовательностью определенного количества битов (определяется максимально возможным количеством факторов риска). Значение каждого бита может быть равно «1», если фактор с соответствующим номером присутствует в данном уравнении регрессии, и «0», если этот фактор отсутствует.
Таким образом, каждой хромосоме соответствует регрессионная модель, построенная методом наименьших квадратов (МНК), с соответствующим ее структуре набором факторов риска.
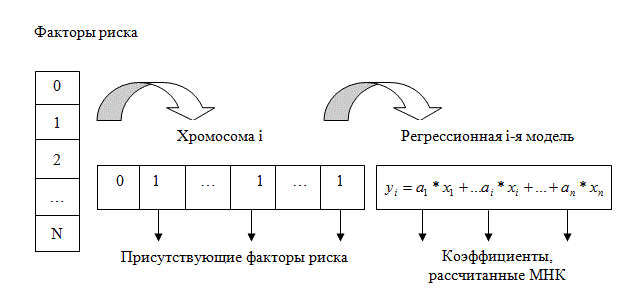
Рисунок 3 – Кодирование хромосомы
- Второй этап подразумевает расчет фитнес-функции. В качестве фитнес-функции выступает ошибка регрессионной модели, которая может рассчитываться по
формуле (1):
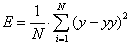 |
(1) |
где N – количество примеров в обучении, y – полученный результат регрессионной модели, yy – действительный результат.
Рассчитанная ошибка сопоставляется каждой хромосоме. Лучшая особь будет иметь минимальную ошибку, то есть минимальную фитнес-функцию.
Третий этап является реализацией генетического алгоритма. Генетические операторы выполняются стандартные.
- Наиболее распространенный метод реализации оператора репродукции (ОР) – построение колеса рулетки, в котором каждой хромосоме соответствует сектор,
пропорциональный ее значению фитнесс-функции, что обеспечивает большую вероятность выбора лучших особей для оператора кроссинговера.
- Применяется простой оператор кроссинговера (ОК), который выполняется в 3 этапа:
1) выбираются две хромосомы (родители) из текущей популяции;
2) случайно выбирается точка скрещивания – число k из диапазона [1,2…n–1], где n – длина хромосомы;
3) две новых хромосомы  ,
,  (потомки) формируются из A и B путем обмена подстрок после точки скрещивания, (рис. 4).
(потомки) формируются из A и B путем обмена подстрок после точки скрещивания, (рис. 4).
ОК выполняется с заданной вероятностью (отобранные два родителя не обязательно производят потомков).

Рисунок 4. Формирование хромосом оператором кроссинговера
- Оператор мутации (ОМ) играет вторичную роль и его вероятность обычно мала. Оператор мутации выполняется в 2 этапа:
1) в хромосоме 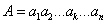 случайно выбирается k-ая позиция (бит) мутации(1 <= k <= n);
случайно выбирается k-ая позиция (бит) мутации(1 <= k <= n);
2) производится инверсия значения гена в k-й позиции, формула (2).
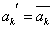 |
(2) |
- Следующий этап алгоритма предполагает расширение популяции за счет добавления новых, только что созданных особей.
- Затем полученную популяцию сокращаем до исходных размеров (работает оператор редукции), путем отбора лучших особей.
- Критериев останова работы алгоритма будет два: максимально заданное количество шагов; незначительное изменение значения фитнес-функции.
- После выполнения критерия останова выполняется поиск лучшей особи в конечной популяции, что является результатом работы алгоритма (уравнение множественной
регрессии). В случае, не выполнения критерия останова, переходим на пункт 2.
Выводы
Рассмотрена актуальная задача выбора лучшей регрессионной модели, для прогнозирования потери крови при родах. В дальнейшем планируется реализовать
рассмотренный математический аппарат и провести эксперименты на реальных медицинских данных, предоставленными сотрудниками центра материнства и детства.
Планируется разработка и внедрение системы поддержки принятия решений (СППР) прогнозирования акушерских кровотечений.
Список использованной литературы
- Д. Рутковская Нейронные сети, генетические алгоритмы и нечеткие системы / Д. Рутковская М. Пилиньский, Л. Рутковский. – М.: 2004. – 452 c.
- Ю.О. Скобцов Основи еволюційних обчислень / Ю.О. Скобцов. – Донецьк: ДонНТУ, 2009. – 316 с.
- Т.А. Васяева Анализ методов отбора факторов риска развития патологий в акушерстве и гинекологии / Т.А. Васяева, Д.Е.
Иванов, И.В. Соков, А.С. Сокова // Збірка матеріалів ІІ Всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених.ІУС
КМ-2011 11–13 квітня 2011р., Донецьк: ДонНТУ, 2011. – № 1. – С. 209–212.
- Т. А. Васяева Отбор факторов риска потери крови при родах / Т.А. Васяева, Д.Е. Иванов, И.В. Соков. // Інтелектуальні
системи прийняття рішень і проблеми обчислювального інтелекту: Матеріали міжнародної наукової конференції. – Херсон: ХНТУ, 2011. –
№ 1. – 472 с.



