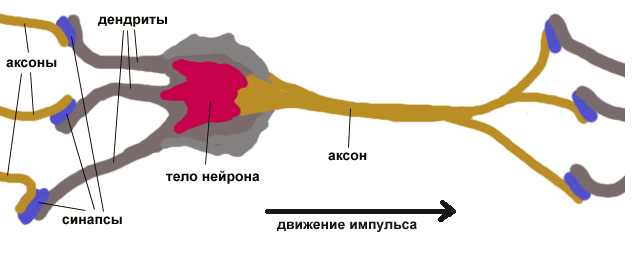
Нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений от нашей кожи, ушей и глаз к мозгу, процессы мышления и управления действиями – все это реализовано в живом организме как передача электрических импульсов между нейронами. Рассмотрим строение биологического нейрона. Каждый нейрон имеет отростки нервных волокон двух типов – дендриты, по которым принимаются импульсы, и единственный аксон, по которому нейрон может передавать импульс. Аксон контактирует с дендритами других нейронов через специальные образования – синапсы, которые влияют на силу импульса.

Можно считать, что при прохождении синапса сила импульса меняется в определенное число раз, которое мы будем называть весом синапса. Импульсы, поступившие к нейрону одновременно по нескольким дендритам, суммируются. Если суммарный импульс превышает некоторый порог, нейрон возбуждается, формирует собственный импульс и передает его далее по аксону. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующего нейрона.
Нетрудно построить математическую модель описанного процесса.
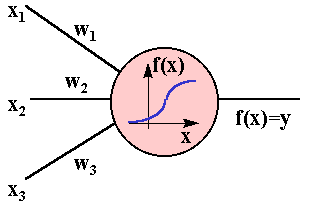
На рисунке изображена модель нейрона с тремя входами (дендритами), причем синапсы этих дендритов имеют веса w1, w2, w3. Пусть к синапсам поступают импульсы силы x1, x2, x3 соответственно, тогда после прохождения синапсов и дендритов к нейрону поступают импульсы w1x1, w2x2, w3x3. Нейрон преобразует полученный суммарный импульс x=w1x1+w2x2+w3x3 в соответствии с некоторой передаточной функцией f(x). Сила выходного импульса равна y=f(x)=f(w1x1+w2x2+w3x3). Таким образом, нейрон полностью описывается своими весами wk и передаточной функцией f(x). Получив набор чисел (вектор) xk в качестве входов, нейрон выдает некоторое число y на выходе.
Искусственная нейронная сеть (ИНС, нейронная сеть) – это набор нейронов, соединенных между собой. Как правило, передаточные функции всех нейронов в нейронной сети фиксированы, а веса являются параметрами нейронной сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы нейронной сети, а некоторые выходы – как внешние выходы нейронной сети. Подавая любые числа на входы нейронной сети, мы получаем какой-то набор чисел на выходах нейронной сети. Таким образом, работа нейронной сети состоит в преобразовании входного вектора в выходной вектор, причем это преобразование задается весами нейронной сети.
Практически любую задачу можно свести к задаче, решаемой нейронной сетью. Далее показано, каким образом следует сформулировать в терминах нейронной сети задачу распознавания рукописных букв.
Дано: растровое черно-белое изображение буквы размером 30x30 пикселов
Надо: определить, какая это буква (в алфавите 33 буквы)
Дано: входной вектор из 900 двоичных символов (900=30x30)
Надо: построить нейронную сеть с 900 входами и 33 выходами, которые помечены буквами. Если на входе нейронной сети изображение буквы А
,
то максимальное значение выходного сигнала достигается на выходе А
. Аналогично нейронная сеть работает для всех 33 букв.
Поясним, зачем требуется выбирать выход нейронной сети с максимальным уровнем сигнала. Дело в том, что уровень выходного сигнала, как правило,
может принимать любые значения из какого-то отрезка. Однако, в данной задаче нас интересует не аналоговый ответ, а всего лишь номер категории
(номер буквы в алфавите). Поэтому используется следующий подход – каждой категории сопоставляется свой выход, а ответом нейронной сети считается
та категория, на чьем выходе уровень сигнала максимален. В определенном смысле уровень сигнала на выходе А
– это достоверность того, что на вход
нейронной сети была подана рукописная буква A
. Задачи, в которых нужно отнести входные данные к одной из известных категорий, называются задачами
классификации. Изложенный подход – стандартный способ классификации с помощью нейронных сетей.
Теперь, когда стало ясно, что именно мы хотим построить, мы можем переходить к вопросу как строить такую нейронную сеть
. Этот вопрос
решается в два этапа:
На первом этапе следует выбрать следующее:
Эта задача на первый взгляд кажется необозримой, но, к счастью, нам необязательно придумывать нейронную сеть с нуля
– существует несколько
десятков различных нейросетевых архитектур, причем эффективность многих из них доказана математически. Наиболее популярные и изученные
архитектуры – это многослойный перцептрон, нейронная сеть с общей регрессией, нейронные сети Кохонена и другие. Про все эти архитектуры скоро
можно будет прочитать в специальном разделе этого учебника.
На втором этапе нам следует обучить
выбранную нейронную сеть, то есть подобрать такие значения ее весов, чтобы она работала нужным образом.
Необученная нейронная сеть подобна ребенку – ее можно научить чему угодно. В используемых на практике нейронных сетях количество весов может
составлять несколько десятков тысяч, поэтому обучение – действительно сложный процесс. Для многих архитектур разработаны специальные алгоритмы
обучения, которые позволяют настроить веса нейронной сети определенным образом. Наиболее популярный из этих алгоритмов – метод обратного
распространения ошибки (Error Back Propagation), используемый, например, для обучения перцептрона.
Обучить нейронную сеть – значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку
изображение буквы А
, мы спрашиваем его: Какая это буква?
Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него
получить: Это буква А
. Ребенок запоминает этот пример вместе с верным ответом, то есть в его памяти происходят некоторые изменения в нужном
направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все 33 буквы будут твердо запомнены. Такой процесс
называют обучение с учителем
.
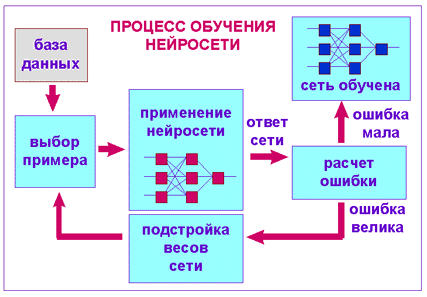
При обучении нейронной сети мы действуем совершенно аналогично. У нас имеется некоторая база данных, содержащая примеры (набор рукописных
изображений букв). Предъявляя изображение буквы А
на вход нейронной сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен
и верный (желаемый) ответ – в данном случае нам хотелось бы, чтобы на выходе нейронной сети с меткой А
уровень сигнала был максимален. Обычно в
качестве желаемого выхода в задаче классификации берут набор (1, 0, 0, ...), где 1 стоит на выходе с меткой А
, а 0 – на всех остальных выходах.
Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем 33 числа – вектор ошибки. Алгоритм обратного распространения
ошибки – это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов нейронной сети. Одну и ту же букву (а также
различные изображения одной и той же буквы) мы можем предъявлять нейронной сети много раз. В этом смысле обучение скорее напоминает повторение
упражнений в спорте – тренировку.
Оказывается, что после многократного предъявления примеров веса нейронной сети стабилизируются, причем нейронная сеть дает правильные ответы на
все (или почти все) примеры из базы данных. В таком случае говорят, что нейронная сеть выучила все примеры
, нейронная сеть обучена
, или
нейронная сеть натренирована
. В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем
выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную
нейронную сеть считают натренированной и готовой к применению на новых данных.
Важно отметить, что вся информация, которую нейронная сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения нейронной сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать нейронную сеть для предсказания финансового кризиса, если в обучающей выборке кризисов не представлено. Считается, что для полноценной тренировки нейронной сети требуется хотя бы несколько десятков (а лучше сотен) примеров.
Повторим еще раз, что обучение нейронных сетей – сложный и наукоемкий процесс. Алгоритмы обучения нейронных сетей имеют различные параметры и настройки, для управления которыми требуется понимание их влияния.
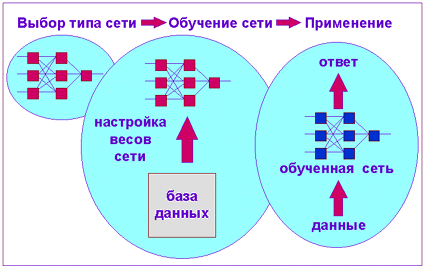
После того, как нейронная сеть обучена, мы можем применять ее для решения полезных задач. Важнейшая особенность человеческого мозга состоит
в том, что, однажды обучившись определенному процессу, он может верно действовать и в тех ситуациях, в которых он не бывал в процессе обучения.
Например, мы можем читать почти любой почерк, даже если видим его первый раз в жизни. Так же и нейронная сеть, грамотным образом обученная, может с
большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Например, мы можем нарисовать букву А
другим почерком, а
затем предложить нашей нейронной сети классифицировать новое изображение. Веса обученной нейронной сети хранят достаточно много информации о
сходстве и различиях букв, поэтому можно рассчитывать на правильный ответ и для нового варианта изображения.
Отметим, что задачи классификации (типа распознавания букв) очень плохо алгоритмизуются. Если в случае распознавания букв верный ответ очевиден для нас заранее, то в более сложных практических задачах обученная нейронная сеть выступает как эксперт, обладающий большим опытом и способный дать ответ на трудный вопрос.
Примером такой задачи служит медицинская диагностика, где нейронная сеть может учитывать большое количество числовых параметров (энцефалограмма,
давление, вес и т.д.). Конечно, мнение
нейронной сети в этом случае нельзя считать окончательным.
Классификация предприятий по степени их перспективности – это уже привычный способ использования нейронных сетей в практике западных компаний. При этом нейронная сеть также использует множество экономических показателей, сложным образом связанных между собой.
Нейросетевой подход особенно эффективен в задачах экспертной оценки по той причине, что он сочетает в себе способность компьютера к обработке
чисел и способность мозга к обобщению и распознаванию. Говорят, что у хорошего врача способность к распознаванию в своей области столь велика,
что он может провести приблизительную диагностику уже по внешнему виду пациента. Можно согласиться также, что опытный трейдер чувствует направление
движения рынка по виду графика. Однако в первом случае все факторы наглядны, то есть характеристики пациента мгновенно воспринимаются мозгом как
бледное лицо
, блеск в глазах
и т.д. Во втором же случае учитывается только один фактор, показанный на графике – курс за определенный период
времени. Нейронная сеть позволяет обрабатывать огромное количество факторов (до нескольких тысяч), независимо от их наглядности – это универсальный
хороший врач
, который может поставить свой диагноз в любой области.
Помимо задач классификации, нейронные сети широко используются для поиска зависимостей в данных и кластеризации.
Например, нейронная сеть на основе методики МГУА (метод группового учета аргументов) позволяет на основе обучающей выборки построить зависимость одного параметра от других в виде полинома. Такая нейронная сеть может не только мгновенно выучить таблицу умножения, но и найти сложные скрытые зависимости в данных (например, финансовых), которые не обнаруживаются стандартными статистическими методами.
Кластеризация – это разбиение набора примеров на несколько компактных областей (кластеров), причем число кластеров заранее неизвестно. Кластеризация позволяет представить неоднородные данные в более наглядном виде и использовать далее для исследования каждого кластера различные методы. Например, таким образом можно быстро выявить фальсифицированные страховые случаи или недобросовестные предприятия.